5233

Robust and fast MCMC sampling of diffusion MRI microstructure models
Robbert Leonard Harms1 and Alard Roebroeck1

1Department of Cognitive Neuroscience, Maastricht University, Maastricht, Netherlands

Synopsis

In this work we extend the Maastricht Diffusion Toolbox (MDT) software package with MCMC capabilities, thereby introducing robust and fast sampling of diffusion MRI microstructure models. MDT's object oriented modular design allows arbitrary specification and combination of models, likelihood functions, prior functions and proposal distributions. GPU based computations allow for ~80x faster MCMC sampling; e.g. the 81 volume example NODDI dataset can be sampled with 15000 samples in 1.5 hour, making MDT suitable for probabilistic inference of all implemented models, both dMRI microstructure as quantitative MRI models. The software is open source and freely available at https://github.com/cbclab.

Introduction

Markov Chain Monte Carlo (MCMC) is a Bayesian sampling technique that can be used to numerically approximate the probability density function and marginal likelihood distributions of a provided posterior function. MCMC output is used in probabilistic tractography1⁠ and can be used for uncertainty estimates and inferring correlations between parameters. In this work we present an extension of the previously presented Maastricht Diffusion Toolbox (MDT)2 to perform GPU (graphics processing unit; graphics card) accelerated MCMC sampling of any implemented diffusion MRI model (like CHARMED3⁠, NODDI4⁠, ActiveAx5⁠, etc.) to complement GPU accelerated non-linear optimization. Using the GPU accelerated routines, MDT can speed up processing by 60~100 times over standard sequential routines, allowing, for example, sampling the NODDI example data4⁠ with 15000 samples per voxel, full brain, in 1.5 hour on a single AMD Fury X graphics card. Optionally, MDT can directly fit a distribution to the acquired samples allowing the user to discard the chain directly after processing, thereby saving considerably on storage requirements. MDT is written in Python and OpenCL and is open source and freely available at https://github.com/cbclab.

Methods

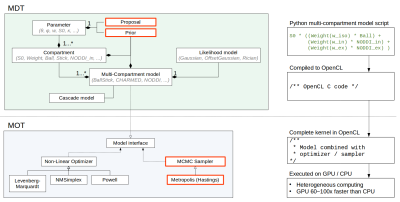
Figure 1 shows a (high level) overview of MDT and the Multithreaded Optimization Toolbox (MOT) with in red the new additions. In MDT, models are built from the bottom up, from parameters to compartments to multi-compartment models. Since MCMC requires, in addition to the model, a prior function and a proposal function, we added these as modular and reusable components to MDT. In turn, we added to MOT a random walk single component updating Metropolis-Hastings sampler with support for adaptive proposals, fully implemented in OpenCL, a standard for GPU and CPU (central processor) parallelized computations. MDT is constructed such that point estimates from optimization can directly be used as starting point for sampling (removing the need for burn-in). Using Multivariate Effective Sample Size (ESS) theory6⁠, MDT can predict per model how many samples are needed to approximate the true posterior density within a specified confidence region with a corresponding precision. For this work we used non-informative priors, initialized the sampler with a Powell point estimate7⁠ and sampled without burn-in and thinning (sub-sampling of the chain). We used a single AMD Fury X graphics card for all processing.

Results and discussion

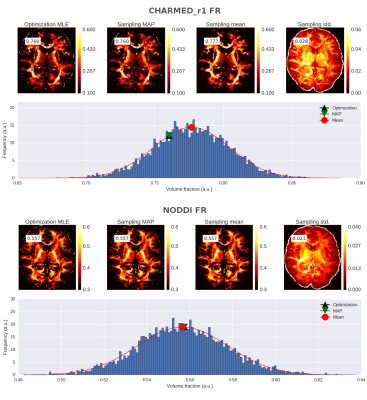
To illustrate MCMC sampling, we fitted and sampled two common models, CHARMED_r1 (with 1 restricted intra-axonal compartments) and NODDI to a single diffusion MRI dataset of the HCP MGH Consortium. This dataset (1003 from the HCP MGH Consortium) was acquired at a resolution of 1.5mm isotropic with 4 shells of b=1000, 3000, 5000, 10,000, s/mm^2, with respectively 64, 64, 128, 256 directions and with 40 b0 volumes. Figure 2 shows the fitting and sampling results of both models over a single slice with for one voxel the sampling chain and corresponding point estimates displayed in a histogram. CHARMED_r1 was sampled with 24000 samples and NODDI with 15000 samples to reach, on average, a multivariate ESS within the 95% confidence region with a 90% precision. As post-processing we fitted a Normal distribution to the marginals of each parameter providing the mean of the distribution. Results show close correspondence between the starting point (given by the optimization routine) and the maximum a posteriori found by the sampler, although some difference can be noted between these two point estimates (essentially the mode of the distribution) and the fitted distribution’s mean. MCMC sampling of this large whole brain dataset took 8 hours for CHARMED_r1 and 2 hours for NODDI. Smaller datasets such as the NODDI example dataset can be sampled with NODDI within 1.5 hours.

Conclusion

We here put forward OpenCL accelerated Monte Carlo Markov Chain (MCMC) processing in MDT thereby combining modular dMRI microstructure modeling with multi-threaded and/or graphics card accelerated sampling. In addition to fast processing, MDT can directly post-process the acquired samples by fitting any choosen distribution to the samples, thereby removing the need to store the full set of samples. With the fast processing and low storage requirements, MCMC can now become a viable method for diffusion microstructure group studies.

Acknowledgements

The research was supported by the Netherlands Organization for Scientific Research (NWO) VIDI 14637 (AR), and the European Research Council Starting Grant, MULTICONNECT #639938 (RH, AR).

References

1. Behrens TEJ, Woolrich MW, Jenkinson M, et al. Characterization and Propagation of Uncertainty in Diffusion-Weighted MR Imaging. Magn Reson Med. 2003;50(5):1077-1088. doi:10.1002/mrm.10609.

2. Harms RL, Roebroeck A. The Maastricht Diffusion Toolbox (MDT): Modular, GPU accelerated, dMRI microstructure modeling. In: ISMRM 2017. ; 2017.

3. Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27(1):48-58. doi:10.1016/j.neuroimage.2005.03.042.

4. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61(4):1000-1016. doi:10.1016/j.neuroimage.2012.03.072.

5. Alexander DC, Hubbard PL, Hall MG, et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage. 2010;52(4):1374-1389. doi:10.1016/j.neuroimage.2010.05.043.

6. Vats D, Flegal JM, Jones GL. Multivariate Output Analysis for Markov chain Monte Carlo. 2015;(1):1-52. http://arxiv.org/abs/1512.07713.

7. Harms RLL, Fritz FJJ, Tobisch A, Goebel R, Roebroeck A. Robust and fast nonlinear optimization of diffusion MRI microstructure models. Neuroimage. 2017;155(October 2016):82-96. doi:10.1016/j.neuroimage.2017.04.064.

Figures

Left, UML diagram of MDT (top) and MOT (bottom) and their interaction, with marked in red the new MCMC sampling functionality. MDT is a modeling toolbox that can construct models out of reusable components. New in this version is the support for priors and proposals making MDT suitable for MCMC sampling. MOT is a general optimization and sampling toolbox with built-in support for multi-threaded CPU and graphic card accelerated computing. The modeling flow on the right shows the use of Python scripting to construct arbitrary multi-compartment models, from which MDT builds the corresponding model equation and uses MOT to optimize or sample the model.

Result slice (row 1 and 3) and sampled posterior (row 2 and 4) of the voxel highlighted in the maps for CHARMED_r1 Fraction Restricted (top) and NODDI Fraction Restricted/weight intra-cellular (bottom). The maps represent, left to right, the Maximum Likelihood Estimated (MLE) FR by the optimizer, the FR of the Maximum a Posteriori (MAP) from MCMC, and the mean and standard deviation of the FR over the marginal. Superimposed In the marginal histogram in red the Gaussian predicted by the sampling mean and std., in green the point estimate of the MAP and in black the point estimate of the optimization MLE of that voxel.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5233