Synopsis

We estimate microstructural features of crossing fascicles using Monte Carlo simulations to represent the diffusion attenuation of each fascicle. The measured diffusion-weighted MRI signal is reconstructed as a sparse weighted sum of pre-computed signals and microstructural properties are estimated from the selected fascicle configurations. The consistent results obtained on various synthetic phantoms as well as on in vivo brain data suggest the potential of our method for the quantitative estimation of microstructural features in fascicle crossings.

Purpose

Monte Carlo (MC) simulations are commonly acknowledged to provide accurate descriptions of the diffusion process. They are often used as a synthetic groundtruth against which closed-form models of the diffusion-weighted MRI (DW-MRI) signal are compared. However, their use as building blocks for the estimation of the tissue microstructure has been scarce and mostly focused on single-fascicle settings^1-3.

We present a framework to estimate microstructural properties of crossing fascicles using sparse optimization on a dictionary of MC signals and assess its performance on synthetic phantoms and in-vivo brain data from the Human Connectome Project (HCP).

Methods

Signal Model

Relying on the validity of the superposition approximation in areas of complex fascicle crossings⁴, we assume that the DW-MRI signal in a voxel$$S=M_0\left[\sum_{k=1}^{K}\nu_kT_kE_k\left(\mathbf{u}_k\right){+}\nu_{\textrm{CSF}}T_{\textrm{CSF}}E_{\textrm{CSF}}\right]$$emanates from the contributions of$$$\,{K}\,$$$fascicles with orientations$$$\,\textrm{u}_k\,$$$and an isotropic CSF compartment, where$$$\,{T}_k=\exp\left(-\textrm{TE}/\textrm{T2}_k\right)\,$$$ is the NMR relaxation at echo time TE and$$$\,{M}_0\,$$$the magnetization at thermal equilibrium. The diffusion attenuations are represented by MC simulations of the diffusion process in substrates typically featuring geometrical arrangements of cylindrical axons^5,6.

Estimation

We performed MC simulations in hexagonal packings^7-9 of straight cylinders to obtain single-fascicle signals for$$$\,{N}=782\,$$$combinations of fascicle-specific radius index$$$\,{r}\,(0.4\mu{m}-7\mu{m};\,$$$steps of$$$\,0.2\mu{m})\,$$$ and density index$$$\,(0.21–0.87;\,$$$steps of$$$\,0.03).\,$$$We used a DIAMOND sub-routine¹⁰ to estimate the number of fascicles and their orientations, rotated the precomputed signals and estimated the microstructural properties of each fascicle in the voxel by solving the sparse optimization problem:$$\begin{equation*}\begin{array}\\\mathbf{w}^*=&\underset{\begin{array}[l]\\\mathbf{w}\geq0\end{array}}{\text{argmin}}&\left\|y-\begin{bmatrix}F_1|\dots|F_K|T_{CSF}E_{CSF}\end{bmatrix}\cdot\begin{bmatrix}\mathbf{w}_1\\\vdots\\\mathbf{w}_K\\w_{CSF}\end{bmatrix}\right\|_2^2\\&&\\&\text{subject}\;\text{to}&\left|\mathbf{w}_k\right|_{0}=1,{\quad}k=1,\dots,K,\\\end{array}\end{equation*}$$where$$$\,y\,$$$are the acquired DW-MRIs and the constraints on$$$\,\mathbf{w}_k\,$$$ guarantee that each fascicle is characterized by only one configuration$$$\,(r,f)$$$ from its sub-dictionary$$$\,F_k=T_k\left[E_1(r_1,f_1,\textrm{u}_k),\dots,E_N(r_N,f_N,\textrm{u}_k)\right]\,$$$. We solved$$$\,(1)\,$$$by selecting the optimal solution$$$\,\left(r_1^*,\dots{,}r_K^*,f_1^*,\dots{,}f_K^*,w_1^*,\dots{,}w_K^*,w_{CSF}^*\right)\,$$$out of$$$\,N^K\,$$$independent$$$\,(K+1)$$$-variable sub-problems:$$\min\limits_{1\leq{i_1,\dots,i_K}\leq{782}}\,\min\limits_{\mathbf{w}\geq{0}}\left\|y-\begin{bmatrix}T_1E(r_{i_1},f_{i_1},\mathbf{u}_1 ),\dots,T_KE(r_{i_K},f_{i_K},\mathbf{u}_K),T_{CSF}E_{CSF}\end{bmatrix}\cdot\begin{bmatrix}w_1\\\vdots\\{w}_K\\w_{CSF}\end{bmatrix}\right\|_2^2.$$

Synthetic Experiments

We focused on the case$$$\,K=2\,$$$ and considered the MGH-USC HCP acquisition protocol¹¹ consisting of 40$$$\,b=0\,$$$images and 4 shells at b-values$$$\,b=1000,3000,5000,10000s/mm^2\,$$$containing respectively 64, 64, 128 and 256 gradient directions; with$$$\,\delta=12.9ms,\Delta=21.8ms.\,$$$We fixed$$$\,\textrm{T2}=70ms\,$$$and$$$\,D=2.0\mu{m}^2/ms\,$$$in the intra- and extra-axonal spaces and$$$\,\textrm{T2}=1ms,D=3.0\mu{m}^2/ms\,$$$in the CSF.

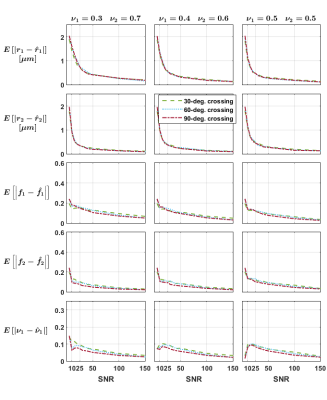
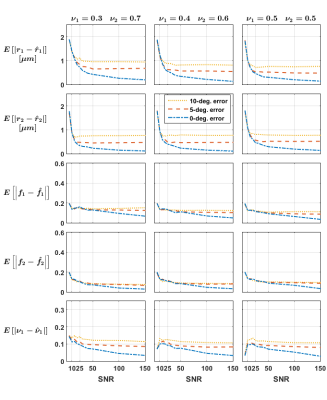
Independent voxels: Signals for 288 crossing configurations were generated subject to the constraints$$$\,r_1=r_2=r;f_1=f_2=f;1\mu{m}\leq{r}\leq{4}\mu{m};0.42\leq{f}\leq{0.84}\,$$$ and crossing angles$$$\,30,60,90^{\circ}\,$$$and rician noise was added to the signals (SNR 5-150, 10 repetitions). We investigated the impact of the groundtruth crossing angle and of initially misestimating the fascicles’ orientations on the mean absolute error (MAE) for each parameter.

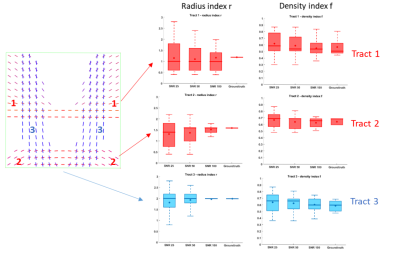
2D phantom: A phantom with more complex configurations$$$\,(r_1\neq{r}_2,f_1\neq{f}_2)\,$$$was created by simulating tracts exhibiting a constant radius index$$$\,r\,$$$and spatially smooth variations of the fascicle-specific density index$$$\,f\,$$$(Figure 3), intersecting at a variety of crossing angles (between 31 et 86°, average 63°). Some voxels also featured single fascicles of axons and CSF partial voluming.

In vivo data

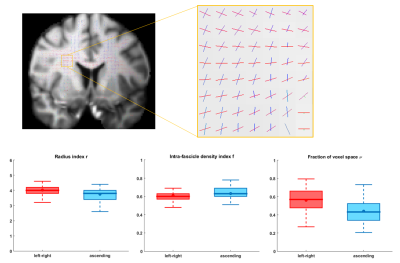
A ROI was selected in the centrum semiovale of one subject from the MGH Adult Diffusion data release¹¹. Tract-specific microstructural properties were estimated on the two fascicles identified by the DIAMOND routine with largest signal weights.

Results and discussion

The estimates obtained on the independent crossings showed relatively large errors in radius index (MAE up to$$$\,2\mu{m}\,$$$whereas groundtruth$$$\,r\leq{4}\mu{m}$$$) and more consistent results in the density index; while suggesting a relatively mild impact of the groundtruth crossing angle (Figure 1). Figure 2 suggests that errors on the fascicles’ directions should be below 5° to avoid asymptotically-biased estimates of the fascicle’s microstructural parameters.

The phantom results are shown in Figure 3. All angular errors made by the DIAMOND sub-routine were bounded by$$$\,1.5^{^\circ}\,$$$and the tract-specific distributions of microstructural parameters$$$\,r\,$$$and$$$\,f\,$$$converged to the groundtruth with increasing SNR, with the slowest convergence occurring for the smaller radius index of Tract$$$\,1(r=1.4\mu{m})\,$$$. The MAEs on$$$\,r\,$$$at SNR=25 for instance were$$$\,0.58,0.51,\,$$$and$$$\,0.42\mu{m}\,$$$for each tract respectively, consistent with the$$$\,0.47\mu{m}\,$$$MAE previously found in the independent voxels with crossing angle$$$\,60^{\circ}\,$$$and no angular error.

The results on the HCP data (Figure 4) suggest that the axons of the horizontal tract (red) have a slightly larger radius index$$$\,r,\,$$$are less densely-packed$$$\,(f)\,$$$and occupy a larger fraction$$$\,\nu\,$$$of the voxel than the axons of the vertical tract (blue). The interquartile ranges of the estimates were small relative to the median values.

Conclusion

Acknowledgements

References

[1] Nilsson, M., Alerstam, E., Wirestam, R., Sta, F., Brockstedt, S., & Lätt, J. (2010). Evaluating the accuracy and precision of a two-compartment Kärger model using Monte Carlo simulations. Journal of Magnetic Resonance, 206(1), 59-67.

[2] Nedjati-Gilani, G. L., Schneider, T., Hall, M. G., Cawley, N., Hill, I., Ciccarelli, O., ... & Alexander, D. C. (2017). Machine learning based compartment models with permeability for white matter microstructure imaging. NeuroImage, 150, 119-135.

[3] Rensonnet, G., Scherrer, B., Warfield, S. K., Macq, B. and Taquet, M., 2017, April. Microstructure imaging from a dictionary of Monte Carlo signals: assessment on a rat model of Wallerian degeneration. In 25th annual meeting of the International Society for Magnetic Resonance in Medicine (ISMRM)

[4] Rensonnet, G., Scherrer, B., Warfield, S. K., Macq, B., & Taquet, M. (2017). Assessing the validity of the approximation of diffusion‐weighted‐MRI signals from crossing fascicles by sums of signals from single fascicles. Magnetic Resonance in Medicine.

[5] Hall, M. G., & Alexander, D. C. (2009). Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE transactions on medical imaging, 28(9), 1354-1364.

[6] Rensonnet, G., Jacobs, D., Macq, B., & Taquet, M. (2015, December). A hybrid method for efficient and accurate simulations of diffusion compartment imaging signals. In 11th International Symposium on Medical Information Processing and Analysis (SIPAIM 2015) (pp. 968107-968107). International Society for Optics and Photonics.

[7] Alexander, Daniel C., et al. "Orientationally invariant indices of axon diameter and density from diffusion MRI." Neuroimage 52.4 (2010): 1374-1389.

[8] Xu, Junzhong, et al. "Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy." NeuroImage 103 (2014): 10-19.

[9] Sepehrband, Farshid, et al. "Towards higher sensitivity and stability of axon diameter estimation with diffusion‐weighted MRI." NMR in Biomedicine 29.3 (2016): 293-308.

[10] Scherrer, B., Schwartzman, A., Taquet, M., Sahin, M., Prabhu, S. P., & Warfield, S. K. (2016). Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion‐compartment imaging (DIAMOND). Magnetic resonance in medicine, 76(3), 963-977.

[11] Setsompop, K., Kimmlingen, R., Eberlein, E., Witzel, T., Cohen-Adad, J., McNab, J. A., ... & Cauley, S. F. (2013). Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage, 80, 220-233.

[12] Auría, A., Romascano, D., Canales-Rodriguen, E., Wiaux, Y., Dirby, T. B., Alexander, D., ... & Daducci, A. (2015, September). Accelerated microstructure imaging via convex optimisation for regions with multiple fibres (AMICOx). In Image Processing (ICIP), 2015 IEEE International Conference on (pp. 1673-1676). IEEE.

[13] Farooq, H., Xu, J., Nam, J. W., Keefe, D. F., Yacoub, E., Georgiou, T., & Lenglet, C. (2016). Microstructure Imaging of Crossing (MIX) White Matter Fibers from diffusion MRI. Scientific reports, 6.

[14] Daducci, A., Dal Palù, A., Lemkaddem, A., & Thiran, J. P. (2015). COMMIT: convex optimization modeling for microstructure informed tractography. IEEE transactions on medical imaging, 34(1), 246-257.