5223

Accurate fibre dispersions from varying the b-tensor shape

Michiel Cottaar¹, Filip Szczepankiewicz^2,3, Matteo Bastiani¹, Stamatios N. Sotiropoulos^1,4, Markus Nilsson², and Saad Jbabdi¹

¹Wellcome Centre for Integrative Neuroscience (WIN) - FMRIB, University of Oxford, Oxford, United Kingdom, ²Clinical Sciences Lund, Department of Radiology, Lund University, Lund, Sweden, ³Random Walk Imaging AB, Lund, Sweden, ⁴Sir Peter Mansfield Imaging Centre, School of Medicine, University of Nottingham, Nottingham, United Kingdom

Synopsis

Accurate measures of fibre dispersion might improve tractography through voxels with bending and/or fanning configurations and also provide more accurate tissue microstructure indices. When estimated from regular diffusion MRI, however, the accuracy of the dispersion estimate depends on the accuracy of the underlying microstructural model. In this work, we find that encoding water diffusion using multiple shapes of the b-tensor leads to an accurate measurement of fibre dispersion within a single b-shell. We show that this holds for complicated sub-voxel geometries using both simulations and in vivo data.

Introduction

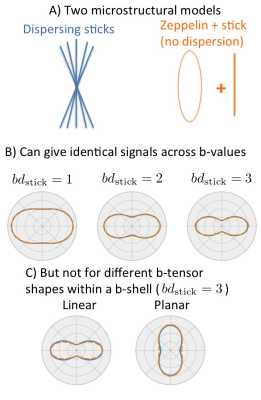
The diffusion MRI (dMRI) signal can be modelled as the convolution of a fibre orientation distribution function (fODF) with a fibre response function. Therefore, measuring the fODF width (fibre dispersion) requires knowing the response function (diffusion anisotropy). This is usually done by either estimating it from the most anisotropic voxels¹ or by assuming an explicit microstructural model^2-4, whereby if the assumptions break down, estimates of fibre dispersion can be biased (Figure 1B) due to model degeneracy^5,⁶.

These models generally only consider data acquired using the Stejskal-Tanner sequence, which is sensitive to diffusion along a single direction (linear tensor encoding). By varying the gradient waveform more generally one can create sequences sensitive to diffusion in a plane (planar encoding) or to diffusion in all directions (spherical encoding)^7,8. Combining these sequences in a single b-shell allows the measurement of anisotropy experienced by water at the microscopic scale independently of the fODF (micro-anisotropy)^8,9. Because micro-anisotropy determines the width of the response function, this combination of sequences should allow us to measure fibre dispersion accurately using a single b-shell (Figure 1C)¹¹ Here we show that this is indeed the case even for voxels with complicated microstructure.

Theory

The linear, planar and spherical tensor encoding can be characterized by a b-tensor^12,13:

$$\mathbf{B}_{\rm linear}=b\hat{\mathbf{g}}\cdot\hat{\mathbf{g}}^T,$$

$$\mathbf{B}_{\rm planar}=\frac{b}{2}(\mathbf{I}-\hat{\mathbf{n}}\cdot\hat{\mathbf{n}}^T),$$

$$\mathbf{B}_{\rm spherical}=\frac{b}{3}\mathbf{I},$$

where $$$b$$$ is the b-value, $$$\hat{\mathbf{g}}$$$ the diffusion gradient direction in the linear encoding, $$$\hat{\mathbf{n}}$$$ is the normal of the plane in planar encoding, and $$$\mathbf{I}$$$ is the 3x3 identity matrix. For a voxel containing multiple compartments (indexed with i) with axisymmetric Gaussian diffusion tensors the attenuation is given by¹³:

$$S(\mathbf{B})=\sum_{i}S_{0, i}e^{-\mathbf{B}\cdot\mathbf{D}_i}=\sum_i S_{0, i} e^{-b d_{\bot, i}} e^{-b(d_{\parallel,i}-d_{\bot,i})\hat{\mathbf{\nu}}_i\cdot \mathbf{B} \cdot \hat{\mathbf{\nu}}_i^T}$$

where $$$d_{\parallel, i}$$$/$$$d_{\bot, i}$$$ is the diffusivity along/across $$$\hat{\mathbf{\nu}}_i$$$. We assume all tensors have the same fODF described by the Bingham distribution:

$$f(\hat{\mathbf{\nu}})=\frac{1}{4\pi{}_1F_1(1/2;3/2;\mathbf{Z})}e^{-\hat{\mathbf{\nu}} \cdot \mathbf{Z} \cdot \hat{\mathbf{\nu}}^T}$$

where the Bingham matrix $$$\mathbf{Z}$$$ describes the orientation, extent, and anisotropy of the fODF and $$${}_1 F_1$$$ is a confluent hypergeometric function. The convolution of the Bingham distribution with the signal attenuation gives²:

$$S(\mathbf{B})=\sum_{i}S_{0,i}e^{-bd_{\bot,i}}\frac{{}_1F_1(1/2;3/2;\mathbf{Z}-b(d_{\parallel,i}-d_{\bot,i})\mathbf{B})}{{}_1F_1(1/2;3/2;\mathbf{Z})}$$

To achieve convergence in a single b-shell we can only fit a single compartment, which gives us an effective amplitude ($$$\overline{S_{0}e^{-bd_{\bot}}}$$$) and anisotropy ($$$\overline{d_{\parallel}-d_{\bot}}$$$) for all compartments:

$$S(\mathbf{B})=\overline{S_{0}e^{-bd_{\bot}}}\frac{{}_1F_1(1/2;3/2;\mathbf{Z}-b(\overline{d_{\parallel}-d_{\bot}})\mathbf{B})}{{}_1F_1(1/2;3/2;\mathbf{Z})}$$

Changing the b-value would alter the relative contributions ($$$S_{0,i}e^{-bd_{\bot,i}}$$$) of the various compartments and hence the effective anisotropy ($$$\overline{d_{\parallel}-d_{\bot}}$$$). We can avoid making assumptions about how anisotropy changes with b-value by fixing the b-value and only varying the shape and orientation of the b-tensor B, to probe the fODF (encoded in $$$\mathbf{Z}$$$). This allows us to measure the fODF even without an accurate model of how the contribution of multiple water compartments changes with b-value.

Data

We acquired linear, planar, and spherical encoding data at an isotropic resolution of 2.5 mm for three b-values of 100, 1000, and 2000 s/mm2 (12 directions each for spherical encoding and respectively 12, 30, and 60 directions for both linear and planar encoding; TE=100ms; TR=4.4s, iPAT=1, FOV=25x25x7.5cm) using a 3T MAGNETOM Prisma with a 20-channel head coil array (Siemens Healthcare GmbH, Erlangen, Germany) with a prototype spin-echo sequence that enables b-tensor encoding

Results: simulations

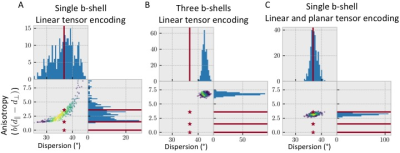
Our hypothesis suggests we can get accurate fibre dispersions even if we make incorrect assumptions about the underlying microstructure. To test this, we generate data for a voxel with three compartments (an isotropic, an anisotropic, and a stick-like one) and fit it using a single anisotropic compartment (i.e., dispersing zeppelins). Results show that a single b-shell is insufficient to constrain this model due to the degeneracy between the anisotropy and the fibre dispersion (Figure 2A). Adding multiple b-shells constrains the model parameters, but gives heavily biased dispersion and anisotropies, because of the mismatch between the assumed and actual microstructural properties (Figure 2B). However, the inclusion of multiple b-tensor shape gives an effective anisotropy, which is a weighted average of the true anisotropies in the various compartments, and the correct fibre dispersion (Figure 2C).

Results: in-vivo data

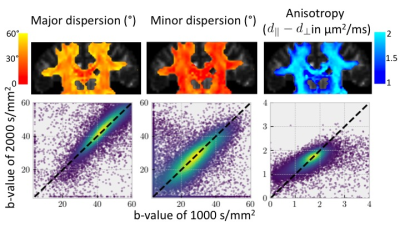
Figure 3 (top) shows initial tests of fitting the dispersing zeppelin model in white matter using the in-vivo linear, planar, and spherical tensor encoding data. Despite the anisotropy being different between the b=1000 and b=2000 shells, the dispersions in the two shells tend to be in agreement (Figure 3 bottom).

Conclusions

The fibre dispersion can be estimated using single b-shell data if several shapes of the b-tensor are used. Simulations suggest that this fibre dispersion estimate can be accurate even if the underlying microstructure is more complicated than assumed in the analysis model in contrast to the traditional approach that only uses linear b-tensor encoding. Initial results on in-vivo diffusion MRI data indicate that the fibre dispersions are in good agreement across b-values.

Acknowledgements

MC is supported by the EPSRC UK (EP/L023067). MB is supported by the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013/ ERC Grant Agreement no. 319456). SJ is supported by the MRC UK (Grant Ref: MR/L009013/1). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). We thank Siemens Healthcare for access to the pulse sequence programming environment.

References

1. Tournier, J. D., Calamante, F. & Connelly, A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35, 1459–72 (2007).

2. Sotiropoulos, S. N., Behrens, T. E. & Jbabdi, S. Ball and rackets: Inferring fiber fanning from diffusion-weighted MRI. Neuroimage 60, 1412–25 (2012).

3. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A. & Alexander, D. C. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61, 1000–16 (2012).

4. Mollink, J. et al. Evaluating fibre orientation dispersion in white matter: Comparison of diffusion MRI, histology and polarized light imaging. Neuroimage (2017). doi:10.1016/j.neuroimage.2017.06.001

5. Novikov, D. S., Jespersen, S. N., Kiselev, V. G. & Fieremans, E. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. ArXiv E-Prints (2016).

6. Schilling, K. G. et al. Histological validation of diffusion MRI fiber orientation distributions and dispersion. Neuroimage (2017). doi:10.1016/j.neuroimage.2017.10.046

7. Eriksson, S., Lasic, S. & Topgaard, D. Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. J Magn Reson 226, 13–8 (2013).

8. Topgaard, D. Multidimensional diffusion MRI. J Magn Reson 275, 98–113 (2016).

9. Cory, D., Garroway, A. & Miller, J. Applications of spin transport as a probe of local geometry. in Abstracts of Papers of the American Chemical Society 199, 105

10. Lasič, S., Szczepankiewicz, F., Eriksson, S., Nilsson, M. & Topgaard, D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Front. Phys. 2, 11 (2014).

11. Szczepankiewicz, F. et al. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage 104, 241–52 (2015).

12. Westin, C. F. et al. Measurement tensors in diffusion MRI: generalizing the concept of diffusion encoding. Med Image Comput Comput Assist Interv 17, 209–16 (2014).

13. Westin, C.-F. et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage (2016). doi:http://dx.doi.org/10.1016/j.neuroimage.2016.02.039

Figures

Figure 1. Planar tensor encoding can distinguish microstructure configurations where linear encoding cannot. We fit a biophysically plausible zeppelin + stick model with no dispersion (orange) to the expected signal of dispersing fibers (blue; models illustrated in panel A). B) For multi-shell linear tensor encoding data this fit is nearly perfect, which implies that these models are degenerate. C) For linear and planar encoding data with the same b-value the best-fit zeppelin + stick model poorly matches the data from the dispersing stick model, which suggest that the inclusion of planar encoding data breaks the degeneracy between these two models.

Figure 2. Recovered dispersion and anisotropy for three different acquisition schemes. Red lines/stars show true parameter values. 300 datasets (120 volumes with SNR=30) were independently fitted using a dispersing zeppelin model to data generated assuming an isotropic CSF compartment ($$$pv=0.2; bd=9$$$), an anisotropic extra-axonal compartment ($$$pv=0.32; bd_\parallel=2.7; bd_\bot=1.2$$$), and a stick-like intra-axonal compartment ($$$pv=0.48; bd_\parallel=3.6$$$).

Figure 3. Top: maps of the dispersion along the major axis of dispersion (left) and the minor axis of dispersion (middle) and the micro-anisotropy (right) measured at b = 2000 s/mm². Bottom: comparison of these parameters with those measured using the shell with b = 1000 s/mm². This simplified model does not include crossing fibres, which leads to large fibre dispersions in most of the brain.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5223