5204
Biases in classical structural parcellation1University of Copenhagen, Copenhagen, Denmark, 2University of Copenhagen and DTU Compute, Copenhagen, Denmark, 3Aarhus University and University of Pittsburgh, Aarhus, Denmark, 4Computer Science, University of Copenhagen, Copenhagen, Denmark
Synopsis
The classical structural parcellation algorithm by Behrens et al1 remains widely used in clinical research, largely thanks to its simplicity and availability in standard MRI processing software. However, its construction and dependency on tractography leads to several biases that can severely affect the conclusions drawn from it, but which are not well known. We illustrate these biases via the original thalamus parcellation experiment on Human Connectome Project (HCP) data3. Based on our experiments, we outline open problems for future structural parcellation algorithms, and possible directions for overcoming them.
Purpose
Structural parcellation aims to segment a target region in the brain (like the thalamus) into sub-regions that connect strongly to specified cortical or subcortical regions, based on DWI tractography. The classical structural parcellation algorithm by Behrens et al1, illustrated in Figure 1, is widely used in clinical research, due to its simplicity and implementation in off-the-shelf imaging software like FSL2. We demonstrate several limitations of the algorithm, which are not commonly known. These limitations form open problems for future structural parcellation algorithms.
Limitation 1: A complete segmentation
The parcellation algorithm classifies every source region (here: thalamic) voxel as being connected to a cortical target region. Such connections do not always exist in a generic parcellation problem. Even when anatomical knowledge indicates that every source region voxel is connected to a target region, as is the case with the thalamus7, it is not given that the data contains sufficiently strong information to actually estimate those connections.
Limitation 2: A hard segmentation
The voting part of the algorithm classifies each voxel in the source region (thalamus) as connected to exactly one target region, which is often an incorrect assumption. First, the voxel sizes in diffusion MRI are large, so partial volume effects are to be expected. More importantly, however, the thalamus is a hub, and we should expect thalamic voxels to connect to multiple cortical (or sub-cortical) regions6,7. The classical parcellation algorithm is by construction not able to detect this.
Limitation 3: Bias by target region size
In the classical algorithm, the source voxels assigned to one specific target region Cj depend also on the other target regions. By changing the remaining target regions, one can change, and in some cases completely remove, the voxels assigned to Cj, as in Figure 1. This constitutes a bias by target region size.
Methods
We perform experiments using HCP subjects3.
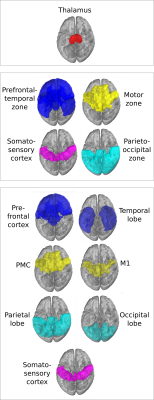
As in the original paper1, parcellation was performed using FSL's probtrackx4,5 for probabilistic tracking, resulting in a per-voxel streamline count for each of the target regions. For every target region, this can be thought of as a connectivity heatmap over the source region (the thalamus). From these, the actual segmentation was computed using FSLs 'find the biggest' command1,5. Two experiments were performed using two nested sets of target regions, shown in Figure 4, as in the original paper1. We compare the final segmentation to its precursor streamline count heatmap by overlaying the heatmap with the segmentation and its complement.
To further assess whether the returned parcellation is supported by the data, the FA was computed and visualized in a representative slice of a randomly selected subject.
Results
Figure 2 shows the parcellations obtained with 4 and 7 target regions in a single HCP subject, compared to the underlying streamline count heatmap. Figure 3 zooms in on the segmentation corresponding to the somatosensory zone for 5 HCP subjects, and illustrates that the segmentation changes between the 4 and 7 target region experiments, although the target region is fixed. The effect is quantitatively confirmed by the differences in number of segmented voxels for the somatosensory region with 4 vs 7 target regions, as reported in the figure caption.
The FA map is found in Figure 5.
Discussion
Limitation 1, namely a complete segmentation, is emphasized by the experiments, which show that the original parcellation algorithm is forced to assign voxels to segments where there is very little support in the data to perform such a segmentation. As shown in Figure 5, the FA is far lower in the interior of the thalamus than near its boundary, although the algorithm also segments the interior.
Limitation 2, namely the hard segmentation, becomes evident in Figure 2, where the data clearly indicates overlapping segments. This is supported by anatomical knowledge of the thalamus 6,7.
Limitation 3, namely bias by region size, is demonstrated in Figure 3, where the thalamus voxels assigned to the somatosensory region depend on the remaining target regions. Using 7 smaller target regions results in a larger segmented thalamic segment although the somatosensory target region stays the same. Logically, we should not expect a change in its corresponding segmentation. This is clearly an unwanted bias, and is precisely the problem sketched in Figure 1.
We conclude that future algorithms should be data-driven, modelling the extent to which the conclusions drawn are supported by the data. We believe that hard segmentations are often too harsh a constraint, and that important future research directions not only include creating soft, possibly uncertain solutions, but also developing statistical methods for population analysis on them.
Acknowledgements
Henrik Thomsen and Michael Hejselbak Jensen had equal contribution to this project.
This research was partially supported by the Centre for Stochastic Geometry and Advanced Bioimaging, funded by a grant from the Villum Foundation.
Data were provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
References
1. T.E.J. Behrens, H. Johansen-Berg, M.W. Woolrich, S.M. Smith, C.A. Wheeler-Kingshott, P.A. Boulby, G.J. Barker, E.L. Sillery, K.Sheehan, O. Ciccarelli, A.J. Thompson, J.M. Brady, P.M. Matthews. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging, Nat Neurosci. 2003 Jul; 6 (7): 750-7
2. M. Jenkinson, C.F. Beckmann, T.E. Behrens, M.W. Woolrich, S.M. Smith. FSL. NeuroImage, 62:782-90, 2012
3. D.C. Van Essen, S.M. Smith, D.M. Barch, T.E.J. Behrens, E. Yacoub, K. Ugurbil, for the WU-Minn HCP Consortium. (2013). TheWU-Minn Human Connectome Project: An overview. NeuroImage 80(2013):62-79
4. T.E.J. Behrens, M.W. Woolrich, M. Jenkinson, H. Johansen-Berg, R.G. Nunes, S. Clare, P.M. Matthews, J.M. Brady, and S.M.Smith. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med, 50(5):1077-1088, 2003
5. T.E.J. Behrens, H. Johansen-Berg, S. Jbabdi, M.F.S. Rushworth, and M.W. Woolrich. Probabilistic diffusion tractography with multiple fibre orientations. What can we gain? NeuroImage, 23:144-155, 2007
6. E.E. Benarroch. Pulvinar: associative role in cortical function and clinical correlations, Neurology. 2015 Feb 17;84(7):738-47
7. E.G. Jones. Principles of thalamic organization, Chapter 3 of The Thalamus, 2nd ed. Cambridge University Press, Cambridge,pp. 87-170, 2007
Figures
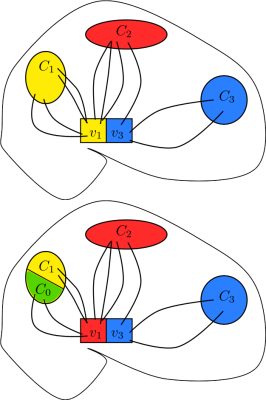
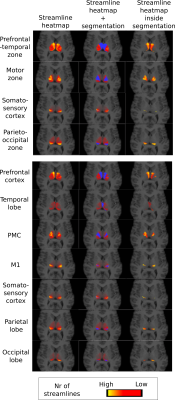
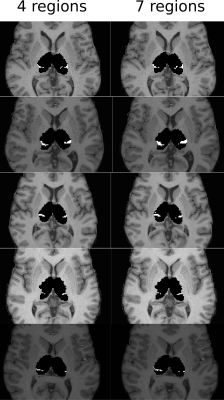
Figure 3: The thalamus segment corresponding to the somatosensory target region for 5 HCP subjects, segmented using 4 and 7 target regions, respectively. While the somatosensory target region was unchanged, the remaining regions were split into smaller regions as in Figure 4. Note how the size bias becomes apparent as an increase in the somatosensory segment when the remaining target regions shrink. The number of voxels in each somatosensory segment above is, for 4 and 7 target regions, respectively, ordered top to bottom: 147/182 (subject133928), 292/360 (subject 118932), 103/130 (subject 111312), 125/182 (subject 110411), 63/120 (subject 100307).