Synopsis

Pulsed chemical exchange saturation transfer (CEST) MRI lacks an analytical solution, impeding data analysis and optimization efforts. A recently proposed solution has mitigated this problem, but it ignores water pool nutation and is thus inaccurate near the water resonance frequency. This work proposes a solution that accounts for water nutation assuming a known flip angle function which can be numerically estimated with no a priori knowledge about tissue parameters. The nutation-corrected solution closely matches numerical Bloch-McConnell simulation, even near the water resonance frequency.

Introduction

Theory & Methods

Chemical exchange saturation transfer (CEST) MRI is sensitive to dilute tissue solutes through their interaction with an exchanging water pool. In CEST, RF irradiation (either continuous wave or pulsed) is played near the resonance frequency of a solute of interest. Solute saturation, and nutation in the case of pulsed CEST methods such as CERT², then transfers to observable water protons and is subsequently imaged.

Our previous work¹ derived an analytical solution to pulsed CEST by approximating the irradiation train as repeated square pulses with equal integrated amplitude (i.e., solute nutation angle) and integrated squared amplitude (i.e., pulse energy) as the true, generally shaped, pulses. The resulting normalized CEST signal is:

$$Z_{pul}^{SS}\approx\frac{P^2R_{1a}}{R_{1\rho,pul}},\tag{1}$$

which is similar to the continuous wave solution³, but in which the projection factor $$$P^2$$$ is a pulsed equivalent,

$$P^2\equiv\mathrm{DC}\mathrm{cos}^2\theta+(1-\mathrm{DC}),\tag{2}$$

and $$$R_{1\rho,pul}$$$ is:

$${R}_{1\rho,pul}={R}_{1\rho}\mathrm{DC}+{R}_{1a}\left(1-\mathrm{DC}\right)+\frac{1}{{t}_{p}+{t}_{d}}{f}_{b}\left(1-{e}^{-{k}_{b}{t}_{d}}\right)\frac{\omega_1^2+\Delta\omega_b^2}{\omega_1^2+\Delta\omega_b^2+k_b^2}\frac{\left(1-e^{-R_{2\rho,b}{t}_{p}}\mathrm{cos}\left(t_p\sqrt{\omega_1^2+\Delta\omega_b^2}\right)-e^{-R_{2\rho,b}{t}_{p}}\left(\frac{k_b}{\sqrt{\omega_1^2+\Delta\omega_b^2}}\right)\mathrm{sin}\left(t_p\sqrt{\omega_1^2+\Delta\omega_b^2}\right)\right)}{\left(1-e^{-R_{2\rho,b}{t}_{p}-k_bt_d}\mathrm{cos}\left(t_p\sqrt{\omega_1^2+\Delta\omega_b^2}\right)+\frac{\Delta\omega_b^2}{\omega_1^2}\left(1-e^{-R_{1\rho,fast}{t}_{p}-k_bt_d}\right)\right)}.\tag{3}$$

Here DC is the irradiation duty cycle; $$$\theta$$$ is the polar angle of the effective field in the rotating frame; $$$R_{1a}$$$ is the water (a-pool, as opposed to solute, b-pool) longitudinal relaxation rate (1/T_1a); $$$R_{1\rho}$$$, $$$R_{2\rho,b}$$$, and $$$R_{1\rho,fast}$$$ are eigenvalues of the continuous wave Bloch-McConnell system; $$$t_p$$$ and $$$t_d$$$ are pulse and delay timings, respectively; $$$f_b$$$ is the dilute solute proton fraction; $$$\omega_1$$$ and $$$\Delta\omega_b$$$ are the irradiation pulse amplitude and offset frequency from the solute resonance, respectively; and $$$k_b$$$ is the solute-water exchange rate.

We extended the previous approach by assuming instantaneous water nutation by a flip angle $$$\alpha(\Delta\omega)$$$ just before each RF irradiation pulse. Following through the previous derivation with this new pulse effect provided the steady-state result

$$Z_{pul,corr}^{SS}\approx\frac{P^2_{corr}R_{1a}}{R_{1\rho,corr}},\tag{4}$$

with nutation-corrected projection factor and $$$R_{1\rho,corr}$$$ given as

$$P^2_{corr}\equiv\mathrm{DC}\mathrm{cos}^2\theta+(1-\mathrm{DC})\mathrm{cos}\alpha,$$

$$R_{1\rho,corr}=R_{1\rho,pul}\mathrm{cos}\alpha+(1-\mathrm{cos}\alpha)R_{1a}\mathrm{DC}\mathrm{cos}^2\theta+\frac{1-\mathrm{cos}\alpha}{t_p+t_d}.\tag{5}$$

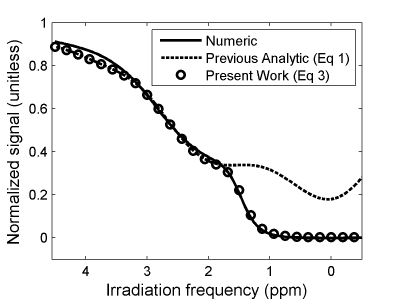
The solution in Equation 4 was compared to that of Equation 1 and numerical Bloch-McConnell solutions assuming R_1a = R_1b = 1s^-1, R_2a = 10s^-1, R_2b = 100s^-1, DC = 61%, t_p + t_d = 5.4ms, k_b = 1000s^-1, and solute resonance offset = +2 ppm to emulate the amine-water exchange system. A high RF irradiation power (equivalent to a 3.6μT continuous wave) was considered in order to challenge the solutions with competing direct and exchange-mediated effects at the solute resonance. The function $$$\alpha(\Delta\omega)$$$ was computed numerically assuming gauss-shaped pulses, but no exchange or relaxation effects and thus no a priori knowledge of the imaging sample.

Results & Discussion

Equation 4 provided accurate results to numerical approaches, even near the water resonance, as seen in Figure 1. Most of the improvement was caused by the inclusion of the rightmost term in $$$R_{1\rho,corr}$$$. The fact that this rate adds linearly to the terms in $$$R_{1\rho,pul}$$$ is similar to the results in previous studies⁴ of continuous-wave CEST, where $$$R_{1\rho}$$$ has linear contributions from distinct physical phenomena. From this perspective, the rate (1−cosα)/(t_p+t_d) is the signal suppression rate caused by water nutation.

The corrected solution still has notable deviations from the numerical results, such as near 4ppm in Figure 1, which may be due to failing to account for pulse shape as experienced by the solute pool. We are currently working to understand and address the source of such deviations.

Conclusion

Acknowledgements

References

1. Gochberg DF, Does MD, Zu Z, et al. Towards an Analytical Solution for Pulsed CEST. NMR in Biomedicine. Under revision.

2. Zu Z, Janve VA, Xu J, et al. A new method for detecting exchanging amide protons using chemical exchange rotation transfer. Magn Reson Med. 2013;69(3):637-647.

3. Zaiss M, Bachert P. Exchange-dependent relaxation in the rotating frame for slow and intermediate exchange - modeling off-resonant spin-lock and chemical exchange saturation transfer. NMR Biomed. 2013;26:507-518.

4. Zaiss M, Zu Z, Xu J, et al. A combined analytical solution for Chemical Exchange Saturation Transfer and semi-solid Magnetization Transfer. NMR Biomed. 2015;28(2):217-230.