5122
Assessment of a clinically feasible Bayesian fitting algorithm using a simplified description of Chemical Exchange Saturation Transfer (CEST) Imaging1Brain Repair and Rehabilitation, University College London, London, United Kingdom, 2Molecular Biotechnology and Health Sciences, University of Torino, Turin, Italy, 3Institute of Biostructure and Bioimaging, University of Torino, Turin, Italy, 4Magnetic Resonance Center, Max-Planck institute for biological cybernetics, Tübingen, Germany
Synopsis
A Bayesian fitting algorithm was combined with analytical approximations of the Bloch-McConnell (BM) equations with the aim to considerably reduce processing time. The accuracy of the algorithm was assessed with simulated data and data from phantom experiments and compared to fit results obtained with the numerical solution of the BM equations. Continuous-wave and pulsed saturation was considered. The results showed agreement between estimates and ground truth as well as between the approximate analytical and numerical model implementations of the Bayesian algorithm. A considerable reduction of processing time was achieved.
Introduction
Chemical Exchange Saturation Transfer (CEST) imaging is a contrast mechanism for molecular imaging with high sensitivity. Bayesian fitting has previously been proposed as an advantageous alternative to traditional least square fitting of Bloch-McConnell (BM) equations to CEST data and has successfully been applied to process in-vivo data 1,2,3. However, increased processing time constitutes the biggest disadvantage and can take several hours per slice. Here, we evaluate the application of Bayesian fitting with simpler analytical solutions of the BM equations which leads to clinically feasible processing times.Methods
A Variational Bayesian (VB) algorithm 3 has previously been successfully applied based on numerical solutions of the BM equations 2. Here, in contrast, we apply the VB algorithm using the following analytical solutions. For continuous-wave (CW) saturation 4:
$$Z(t)=(P_{z}P_{z_{\text{eff}}}-Z_{\text{SS}})e^{\lambda t }+Z_{\text{SS}},$$
with normalized magnetization $$$Z(t)$$$ at time $$$t$$$, steady-state magnetization $$$Z_{\text{SS}}$$$, eigenvalue $$$\lambda$$$ and projection factors $$$P_{z}$$$ and $$$P_{z_{\text{eff}}}$$$.
For pulsed saturation, a solution based on the following equation was used 5:
$$Z(n)=(Z_{\text{i}}-Z_\text{SS})e^{-R_{1\text{a}}t_{\text{d}}n}e^{-R_{1\rho} t_{\text{p}}n}+Z_{\text{SS}},$$
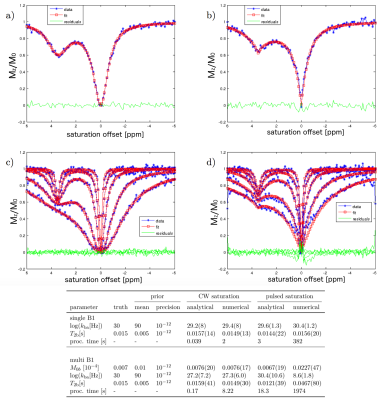
with number of pulses $$$n$$$ , pulse width $$$t_{\text{p}}$$$ , pulse delay $$$t_{\text{d}}$$$ , longitudinal relaxation rate of water $$$R_{1\text{a}}$$$, spin-lock relaxation rate $$$R_{1\rho}$$$ and initial magnetization $$$Z_{\text{i}}$$$. To assess convergence of the algorithm and the reduction of processing time, CEST-spectra of an amide solution (equilibrium magnetisations of water $$$M_{0\text{a}}=1$$$ and amide $$$M_{0\text{b}}=0.007$$$, water relaxation times $$$T_{1\text{a}}=3\text{s}$$$, $$$T_{2\text{a}}=1.5\text{s}$$$, offset = 3.5ppm, amide relaxation times $$$T_{1\text{b}}$$$=1s, $$$T_{2\text{b}}=0.015\text{s}$$$, exchange rate = 30Hz) were simulated by numerical evaluation of the BM equations and fit. CW (single block-pulse of 10s duration) and pulsed saturation (50 Gaussian pulses of 0.1s duration) schemes were considered. Saturation power was varied ($$$B_1$$$ = 0.5,1.0,2.0,5.0 and 10.0μT).
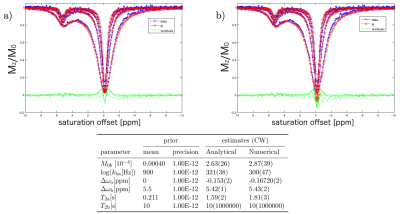
A 15mM Iodipamide in phosphate-buffered saline (PBS) phantom was measured on a 7T scanner at varying saturation powers and CW saturation scheme ($$$B_1$$$ = 1.5, 2.0, 3.0, 6.0μT, pH = 7.4, temperature = 37°C, offsets from -10 to 10ppm in steps of 0.1ppm).
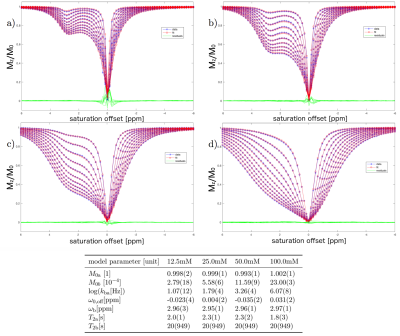
Pulsed saturation data was obtained from 12.5, 25.0, 50.0 and 100.0mM Taurine solutions at 9.4T (0.1% PBS, $$$B_1$$$= 0.78, 1.17, 1.57, 1.96, 2.35, 2.74, 3.13, 3.52, 3.91, 4.31μT, pH = 6.2, temperature T = 23°C, 77 equally spaced offsets between −6 and 6ppm. 151 Gaussian pulses of duration 0.05s were applied with a duty cycle of 0.98.
For comparison, the Z-spectra from the phantom measurements were fitted with the numerical and simplified analytical equations in the Bayesian framework. $$$T_{1\text{a}}$$$ was determined separately with an inversion recovery sequence. Flat priors were assumed for the fit parameters.
Results
The simulated CEST-spectra and fit results of the VB algorithm with simplified analytical solutions can be seen in Figure 1 for CW and pulsed saturation. The fits describe the data well. Parameter estimates agreed with the ground truth. The processing time was reduced by a factor of about 50 for CW saturation and a factor of more than 100 for pulsed saturation data. Iodipamide Z-spectra, fits and parameter estimates are shown in Figure 2. Both algorithms led to matching estimates for concentration and exchange rate. The fits of the Taurine data and the corresponding parameter estimates are shown in Figure 3. The data is described well and residuals are negligible, except close to on resonance at small concentrations. As expected, the equilibrium magnetization determined by the fit is proportional to the Taurine concentration.Discussion
The results show that a considerable reduction of the processing time can be achieved without significant loss of accuracy. In fact, we observed an improved convergence behaviour of the modified algorithm in cases where $$$T_{2\text{a}}$$$ is in the order of the saturation time. The differences of parameter estimates observed when comparing both algorithms are negligible against the errors typically observed in in-vivo experiments, e.g. due to spill-over, or due to an unknown number of pools in the model. The widths of the resulting uncertainty intervals are also comparable between both algorithms, thus preserving all information about the posterior distributions. The main limitation of the approach is that the analytical approximation is valid only for slow and intermediate exchange rates. Parameter estimates might be biased for CEST agents with fast exchange.Conclusion
A considerable reduction of processing time can be achieved with the suggested approach. Especially pulsed saturation data can be processed much faster so that typical clinical images can be evaluated in minutes rather than hours. The application of future improved analytical solutions in the Bayesian fitting framework might further increase the accuracy of the fit.Acknowledgements
AK is supported by Olea Medical® and the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/L016478/1). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 667510 and the Department of Health’s NIHR-funded Biomedical Research Centre at University College London.References
1. Murase K, Tanki N. Numerical solutions to the time-dependent Bloch equations revisited. MRI. 2011;29(1):126-131.
2. Chappell MA, Donahue MJ, Tee YK, et al. Quantitative Bayesian Model-Based Analysis of Amide Proton Transfer MRI. MRM. 2013;70(2):556–567.
3. Chappell MA, Groves AR, Whitcher B,et al. Variational Bayesian Inference for a Nonlinear Forward Model. IEEE. 2009;57(1):223-236.
4. Zaiss M, Bachert P. Exchange–dependent relaxation in the rotating frame for slow and intermediate exchange – Modeling off-resonant spin-lock and chemical exchange saturation transfer. NMR Biomed. 2012:26(1):507-518.
5. Roeloffs V, Meyer C, Bachert P, Zaiss M. Towards quantification of pulsed spinlock and CEST at clinical MR scanners: an analytical interleaved saturation–relaxation (ISAR) approach. NMR Biomed. 2014:28(1): 40–53.
Figures