5101

Contrast source inversion global Maxwell tomography: a technique for electric properties MR imaging without phase information.

Alessandro Arduino^1,2, Oriano Bottauscio², and Luca Zilberti²

¹Dipartimento Energia, Politecnico di Torino, Torino, Italy, ²Metrologia per la qualità della vita, Istituto Nazionale di Ricerca Metrologica (INRiM), Torino, Italy

Synopsis

The possibility to perform MR imaging of the electric properties relying only on the measurable magnitude of transmit sensitivity, without any hypothesis on its phase, is an extremely interesting task pursued by the scientific community in the last years. Here, the adoption of the contrast source inversion technique in the context of the global Maxwell tomography is proposed. The lack of phase information affect the numerical minimisation procedure by introducing local minima in the cost functional. The convergence of the method is restored by the adoption of multi-channel transmit coils, which can increase the data by measuring multiple transmit sensitivities.

Introduction

The possibility to estimate the spatial distribution of both the electric properties, conductivity $$$\sigma$$$ and permittivity $$$\varepsilon$$$, of a human body from magnetic resonance imaging (MRI) scans has drummed up the scientific interest in the last years. Up to now, a plethora of techniques has been proposed for this quantitative imaging, and, usually, they are all referred to with the generic name of magnetic resonance-based electric properties tomography (MREPT). The core of all MREPT implementations is the (direct or not) evaluation of the curvature of the transmit sensitivity map $$$B_1^+$$$,¹ and most of them assumes that both the magnitude and the phase of $$$B_1^+$$$ are known. However, with the exception of few particular situations employing special coils and symmetries,^2,3 MRI cannot measure the absolute phase of the transmit sensitivity.⁴ The first MREPT technique avoiding phase information has been the local Maxwell tomography (LMT),^5,6 which elaborates locally the measurements performed by multi-channel transceive coils in order to estimate the gradient of the absolute phase as well as the electric properties. More recently, the global Maxwell tomography (GMT) has been proposed as a minimisation problem with respect to the transmit sensitivity magnitude only.⁷ Here, in analogy to the contrast source inversion electric properties tomography (CSI-EPT) method,^8,9 an implementation of GMT by the contrast source inversion (CSI) method¹⁰ is proposed and denoted by CSI-GMT. The main advantage of CSI-GMT is the recovery, alongside the electric properties, of an auxiliary unknown $$${\bf w}$$$ directly related to the electromagnetic field and so very useful also for MRI safety applications.¹¹

Methods

As usual in CSI, the unknowns of CSI-GMT are the contrast $$$\chi=(\varepsilon-\varepsilon_0+\text{i}\sigma/\omega)/\varepsilon_0$$$ and the contrast source $$${\bf w}=\chi{\bf E}$$$, where $$$\varepsilon_0$$$ is the permittivity of vacuum and $$${\bf E}$$$ is the electric field generated by the RF coil. The unknown quantities are estimated by minimising a cost functional $$$F[{\bf w},\chi]=F_{\text{d}}[{\bf w}]+F_{\text{o}}[{\bf w},\chi]$$$, which is defined as combination of a couple of contributions. On the one hand, the object error $$$F_{\text{o}}[{\bf w},\chi]$$$ quantifies the discrepancy between the guess input and the incident field as already defined for CSI-EPT.⁹ On the other hand, the data error changes with respect to that of CSI-EPT involving only the magnitude of the transmit sensitivity $$F_{\text{d}}[{\bf w}]=\frac{\left\||B_1^+|^2-|\mu_0\mathcal{S}_{\text{h}}^+{\bf w}+B_1^{+;\,\text{i}}|^2\right\|^2}{2\ \left\||B_1^+|^2-|B_1^{+;\,\text{i}}|^2\right\|^2}\,,$$ where $$$\mu_0\mathcal{S}_{\text{h}}^+$$$ is the linear operator that compute the scattered transmit sensitivity given a contrast source and $$$B_1^{+;\,\text{i}}$$$ is the incident transmit sensitivity. The whole cost functional is minimised numerically adopting a two-step alternating conjugate gradient method. Despite the more complicated data error, the gradient of the cost functional with respect to the contrast source can be computed analytically as in CSI-EPT.⁹ The same applies to the optimal step-length of the conjugate gradient method. As is the case with CSI-EPT, CSI-GMT can be extended trivially to the case of multiple transmit sensitivities measurements,^8,12 as could be when multi-channel transmit coils are employed.¹²

Results and discussion

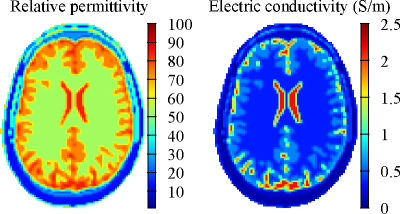
The proposed CSI-GMT method is numerically tested on a realistic two-dimensional model problem, in which a section of the head of the anatomical human model Duke¹³ is studied (Fig. 1). The initial guess of the iterative procedure $$${\bf w}^0$$$ is obtained assuming that the head is homogeneous with the mean properties of the white matter and that the electric field coincides with the incident electric field. 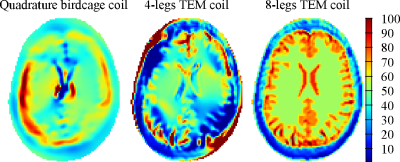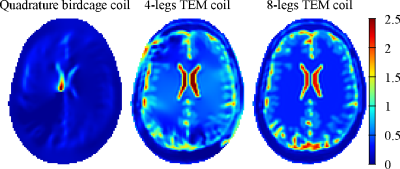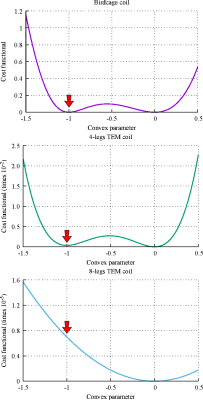A 16-legs quadrature birdcage coil is modelled by 16 line sources driven at 128 MHz and disposed uniformly on a circumference.¹² Similarly, the legs of TEM coils, with as many channels as legs, are modelled with couples of line sources with opposite directions disposed on concentric circumferences.¹² When the noise-free transmit sensitivity simulated for the quadrature birdcage coil is used, the CSI-GMT method does not converge to the correct solution neither in relative permittivity (Fig. 2) nor in electric conductivity (Fig. 3). Actually, the method get stuck in a local minimum of the cost functional (Fig. 4). When the sensitivities of a 4-legs TEM coil are used, the method still get stuck in a local minimum (Fig. 4), but it is closer to the actual distributions (Figs. 2,3). Finally, by increasing the transmit channels up to eight, the CSI-GMT procedure converges correctly to the global minimum (Figs. 2-4).

Conclusion

It has been shown that GMT could be efficiently implemented using the CSI method. The technique is strongly affected by the lack of $$$B_1^+$$$ phase, which can be compensated, anyway, by the employment of multiple measurements performed with multi-channel transmit coils. In order to make CSI-GMT feasible with few channels, the possibility to use some a priori knowledge should be investigated.

Acknowledgements

No acknowledgement found.

References

1. Katscher U, van den Berg CAT. Electric properties tomography: Biochemical, physical and technical background, evaluation and clinical applications. NMR in Biomed. 2017;e3729.

2. Katscher U, Voigt T, Findeklee C, et al. Determination of electric conductivity and local SAR via B1 mapping. IEEE Trans on Med Imag. 2009;28(9):1365-1374.

3. Zhang X, van de Moortele P-F, Schmitter S, He B. Complex B1 mapping and electrical properties imaging of the human brain using a 16-channel transceiver coil at 7T. Magn Reson in Med. 2013;69(5):1285-1296.

4. Wiesinger F, Seifert F, Koenig H, Pruessmann KP. Prospects of absolute B1 calibration. ISMRM 2006. Url: http://cds.ismrm.org/protected/Unsolved_Problems/MC62/. Accessed November, 2017.

5. Sodickson DK, Alon L, Deniz CM, at al. Local Maxwell tomography using transmit-receive coil arrays for contact-free mapping of tissue electrical properties and determination of absolute RF phase. ISMRM 2012, 387.

6. Sodickson DK, Alon L, Deniz CM, et al. Generalized local Maxwell tomography for mapping of electrical property gradients and tensors. ISMRM 2013, 4175.

7. Serrallés JEC, Daniel L, White JK, et al. Global Maxwell tomography: A novel technique for electrical properties mapping based on MR measurements and volume integral equation formulations. Proceedings of IEEE APSURSI International symposium 2016. 2016:1395-1396. Art. no. 7696404.

8. Balidemaj E, van den Berg CAT, Trinks J, et al. CSI-EPT: A contrast source inversion approach for improved MRI-based electric properties tomography. IEEE Trans on Med Imag. 2015;34(9):1788-1796.

9. Arduino A, Zilberti L, Chiampi M, Bottauscio O. CSI-EPT in presence of RF-shield for MR-coils. IEEE Trans on Med Imag. 2017;36(7):1396-1404.

10. Van den Berg PM, Abubakar A. Contrast source inversion method: state of art. PIER. 2001;34:189-218.

11. Arduino A, Chiampi M, Zilberti L, Bottauscio O. Alternative approaches to magnetic resonance-based electric properties tomography and local specific absorption rate estimation. IEEE Trans on Magn. 2017;53(2):5100108.

12. Arduino A, Chiampi M, Pennecchi F, et al. Monte Carlo method for uncertainty propagation in magnetic resonance-based electric properties tomography. IEEE Trans on Magn. 2017;53(11):5100304.

13. Gosselin M-C, Neufeld E, Moser H, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: The Virtual Population 3.0. Phys in Med and Bio. 2014;59(18):5287-5303.

14. IT’IS Foundation. Database for thermal and electromagnetic parameters of biological tissues. Url: http://www.itis.ethz.ch/database. Accessed November, 2017.

Figures

Maps of the actual electric properties in the considered section of the head. Corpus callosum is clearly visible. The properties are assigned in accordance to the IT’IS Foundation database.¹⁴

Maps of the relative permittivity recovered by 1000 steps of CSI-GMT when the simulated magnitude of the transmit sensitivity of a quadrature birdcage coil (left), the magnitudes of the sensitivities of a multi-channel 4-legs TEM coil (centre) and the ones of a 8-legs TEM coil (right) are used as noise-free input.

Maps of the electric conductivity (in S/m) recovered by 1000 steps of CSI-GMT when the simulated magnitude of the transmit sensitivity of a quadrature birdcage coil (left), the magnitudes of the sensitivities of a multi-channel 4-legs TEM coil (centre) and the ones of a 8-legs TEM coil (right) are used as noise-free input.

Trends of the cost functional along a segment passing through the couple recovered after 1000 steps of CSI-GMT and the actual solution. The input transmit sensitivity is provided by a quadrature birdcage coil, a multi-channel 4-legs TEM coil or an 8-legs TEM coil. The convex parameter is such that zero corresponds to the actual solution, whereas -1 corresponds to recovered minimum (indicated by the red arrows). The trends suggest that in the first two cases the numerical procedure get stuck in local minima, whereas the global minimum is reached for the 8-legs TEM coil.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5101