5098

Spatial resolution of Full cr-MREPT: 2D and 3D evaluation
Yusuf Ziya Ider1, Celik Boga1, and Gulsah Yildiz1

1Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey

Synopsis

Determining the spatial resolution (SR) of Magnetic Resonance Electrical Property Tomography (MREPT) is important for assessing its utility in clinical applications. This study aims at finding the SR of Full cr-MREPT which yields images without internal boundary artifact. It is shown by simulations and experimental results that SR in general is determined by the resolution of the MR data. With noise-free simulation data SR is 2-2.5 pixels. With noisy and real data it may go up to 4-4.5 pixels due to Low Pass filtering and regularization. SR appears to be equal in all three directions.

Introduction

Convection-reaction equation based Magnetic Resonance Electrical Properties Tomography (cr-MREPT) aims at reconstructing EPs without internal boundary artifacts1,4. Spatial resolution (SR) is a measure of the ability to identify and separate high contrast small objects. High SR is important e.g. to delineate within-tumour conductivity variations or for brain imaging where small sulci and gyri dominate. Phase-based cr-MREPT has good SR but exhibits a global concave bias on conductivity values2,4. This study aims at studying SR of Full cr-MREPT1 which uses both the magnitude and the phase of $$$B_1^+$$$ and which is more accurate due to less stringent assumptions.

Methods

Full crMREPT eliminates internal boundary artifacts by solving the equation $$$\beta\cdot\triangledown{u}+(\triangledown^2H^+)u-j\omega\mu_0H^+=0$$$ for $$$u$$$ which is the admittivity, $$$u=(\sigma+j\omega\epsilon)^{-1}$$$, and $$$\beta\cdot\triangledown{u}$$$ is the convection term with $$$\beta=\left[\frac{\partial{H^+}}{\partial{x}}-j\frac{\partial{H^+}}{\partial{y}}+\frac{1}{2}\frac{\partial{H_z}}{\partial{z}},{j}\frac{\partial{H^+}}{\partial{x}}+\frac{\partial{H^+}}{\partial{y}}+j\frac{1}{2}\frac{\partial{H_z}}{\partial{z}},\frac{\partial{H^+}}{\partial{z}}-\frac{1}{2}\frac{\partial{H_z}}{\partial{x}}-j\frac{1}{2}\frac{\partial{H_z}}{\partial{y}}\right]^T$$$.

For z-independent $$$u$$$ distributions the third row of the above PDE may be neglected and the problem reduces to 2D. Also in many cases, such as with birdcage volume excitation, the derivatives of $$$H_z$$$ are neglected1,7. The object is assumed to be composed of axial slices of equal distance between them in the z-direction. In case of a 2D application the Region of Interest (ROI) in a certain axial slice is discretized with a triangular mesh. For a 3D application the ROI selected on a certain slice is extended up and down for a specified number of axial slices. For regularization purposes a diffusion term $$$c_{diff}\triangledown^2u$$$ is added to the LHS where the diffusion constant $$$c_{diff}$$$ is experimentally found. Simulations are performed by COMSOL Multiphysics® (COMSOL AB, Sweden) where conductive objects are placed in a QBC coil6.

Results

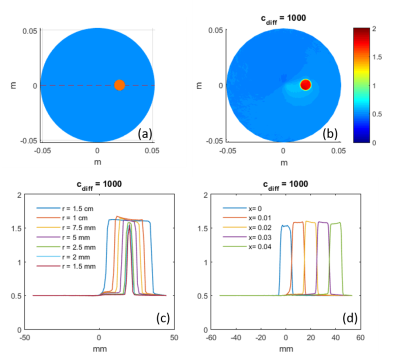
The capability of cr-MREPT to reconstruct conductivity of a single high contract object is shown in Figure-1. In this simulation there is no z-dependence of conductivity and therefore 2D cr-MREPT is used. Conductivity is reconstructed without boundary artifact and also accurately except for small objects (smaller than 3 mm radius). It also appears that reconstructions are not position dependent as the anomaly is moved from center to periphery.

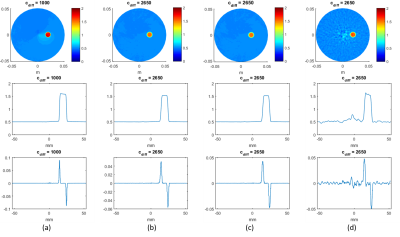
Point Spread Function (PSF) is obtained by taking the spatial derivative of the profiles shown in Figure-1 (see Figure-2). From the PSF, SR is calculated as the FWHM value and is found to be about 1.4 mm which is 2.3 times the pixxel size of 0.6 mm (Data are imported from Comsol environment on a Cartesian grid of 0.6mm voxel size in all directions). When a Gaussian 5x5 low pass filter with s.d. of 1.5 pixels or 3 pixels is used SR becomes 2 mm or 2.4 mm respectively. It is also found that an increase in $$$c_{diff}$$$ does not alter SR much except that it is useful to combat the so called "LCF artifact" especially when data are noisy1. In such case SR is the same but there is more irregularity in the center of the phantom where the Low Convective Field region is (region where $$$\beta$$$ is low).

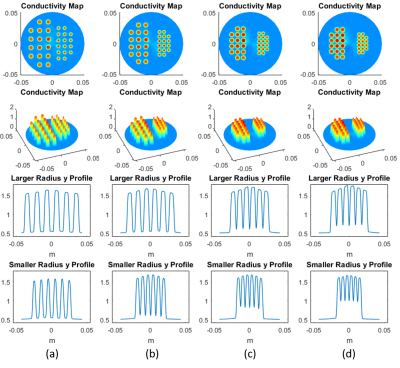
Another approach to evaluating SR is to use arrays of small objects (with 7mm and 5mm diameters) as shown in Figure-3. As the separation between them is narrowed, the reconstructed small objects interfere, but still 1 mm narrow gaps are detected. Importantly, the method does not diverge but tends to smooth the high variations.

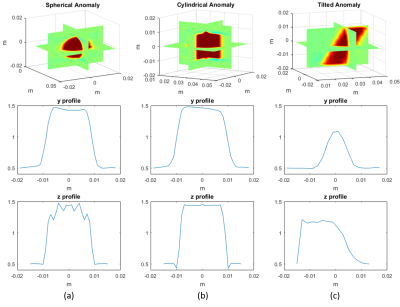
Results of simulations for 3D objects are shown in Figure-4. It is found that the performance of the method w.r.t. boundary artifact and SR is similar in the z-direction. SR is again 2-2.5 pixels in line with 2D simulations.

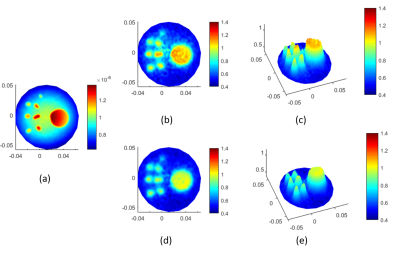
Results for a cylindrical experimental 2D phantom are shown in Figure-5. For $$$B_1^+$$$ phase imaging 2D SSFP is applied with QBC body coil for both transmission and reception. For $$$B_1^+$$$ magnitude mapping QBC is used for transmission and 4-channel head coil is used for reception via double angle method5. BaTiO3 pads were placed on the left or right sides to obtain two sets of data in order to apply the padding method explained previously3 to eliminate LCF artifact. Reconstructions made by combining the two data sets show good contrast and an SR similar to simulations.

Discussion and Conclusion

Full cr-MREPT has good SR which is 2-2.5 times the resolution of the MR data in case of no noise. Most of this is due to the Laplacian and derivative operators applied to $$$H^+$$$. However for noisy data 4-4.5 pixel SR values are observed mostly due to the required Low Pass Filter. Similar SR values are observed in all of x-, y-, and z-directions. It is also observed that the method yields smoothed conductivity distribution in case of variations smaller than the SR value.

Acknowledgements

This study is supported by TUBITAK 114E522 grant. MR experiments are conducted in UMRAM, Bilkent, Ankara.

References

1. Hafalir FS, Oran OF, Gurler N, Ider YZ. Convection-reaction equation based magnetic resonance electrical properties tomography (cr-MREPT). IEEE Trans Med Imag 2014;33:777–793.

2. Yusuf Ziya Ider, Gokhan Ariturk, and Gulsah Yildiz. Spatial and Contrast Resolution of Phase Based MREPT. Proc. Intl. Soc. Mag. Reson. Med. 24 (2016), 3642

3. Gulsah Yildiz, Gokhan Ariturk, and Yusuf Ziya Ider. Use of Padding to Eliminate Low Convective Field Artifact in Conductivity Maps Obtained by cr-MREPT. Proc. Intl. Soc. Mag. Reson. Med. 24 (2016), 1949

4. Necip Gurler and Yusuf Ziya Ider. Gradient-Based Electrical Conductivity Imaging Using MR Phase. Magn. Reson. Med. Magnetic Resonance in Medicine 77:137–150 (2016) DOI: 10.1002/mrm.26097

5. Ulrich Katscher, Dong-Hyun Kim, and Jin Keun Seo. Recent Progress and Future Challenges in MR Electric Properties Tomography. Computational and Mathematical Methods in Medicine,Volume 2013 (2013), Article ID 546562, 11 pages, http://dx.doi.org/10.1155/2013/546562

6. Gurler N, Ider YZ. Numerical methods and software tools for simulation, design, and resonant mode analysis of radio frequency birdcage coils used in MRI. Concepts Magn Reson Part B 2015;45:13–32.

7. U. Katscher, T. Voigt, C. Findeklee, P. Vernickel, K. Nehrke and O. Dossel, "Determination of Electric Conductivity and Local SAR Via B1 Mapping", IEEE Transactions on Medical Imaging, vol. 28, no. 9, pp. 1365-1374, 2009.

Figures

Figure 1: a) Central slice of the cylindrical phantom (radius 6 cm and height 15 cm) with background conductivity of 0.5 S/m and a small anomaly with 1.5 S/m and 5 mm radius. b) Reconstructed conductivity using 2D cr-MREPT. Diffusion constant of $$$c_{diff}=1000$$$ is used. c) Conductivity reconstruction profiles along the line shown in a) and with the radius of anomaly changed as 15, 10, 7.5, 5, 2.5, 2 and 1.5 mm. d) Conductivity reconstruction profiles along the line shown in a) for 5 mm radius anomaly as moved from periphery to center at 1 cm steps.

Figure 2: Conductivity reconstructions, profiles and PSFs for 5 mm radius anomaly placed at 2 cm from center under different low pass filter, diffusion constant and noise conditions: a) Without low pass filter and $$$c_{diff}=1000$$$. b) With 5x5 Gaussian filter with standard deviation of 1.5 pixels and $$$c_{diff}=2650$$$. c) With 5x5 Gaussian filter with standard deviation of 3 pixels and $$$c_{diff}=2650$$$. d) With additive noise (SNR=300 for H+ magnitude and SNR=400 for H+ phase1) and with same settings as in c).

Figure 3: Investigation of SR using small object arrays. a) 7mm and 5mm diameter object arrays with distance between them equal to 7mm and 5mm respectively. Profile plots are for the lines through the centers of 7mm objects in the middle column and also for the 5mm objects in the middle column. b) Same as in a) except the distances between objects are 5 mm and 2.5 mm. c) Same as in a) except the distances between objects are 2.5mm and 1.5mm. d) Same as in a) except the distances between objects are 2mm and 1mm.

Figure 4: Simulation results for 3D objects: a) For a spherical anomaly, reconstructed conductivity, its profile along y axis, and its profile along z-axis respectively from top to bottom. b) For a rectangular anomaly, reconstructed conductivity, its profile along y axis, and its profile along z-axis. c) For a tilted rectangular anomaly, reconstructed conductivity, its profile along y axis, and its profile along z-axis. Data are exported from Comsol environment on a 1 mm Cartesian grid for cases a) and b), and with 2 mm for case c).

Figure 5: Reconstructions for a cylindrical agar phantom with Radius = 6cm and Height = 18cm. Background is (20g/L agar, 2g/l NaCl, 0.2g/L CuSO4). Holes with different sizes are drilled longitudinally and filled with salt solution (6g/L NaCl, 0.2g/L CuSO4). SSFP is used for phase imaging (1.4x1.4x3mm3 voxel size, FA=40°, TR=4.42ms, TE=2.21 ms, NEX=32) and GRE is used for B1+ mapping with double angle method (Voxel size 1.4x1.4x3mm3, TR=2500ms, TE=5ms, FA=60° and NEX=4) a) SSFP magnitude image, b,c) Conductivity reconstructions, d,e) Conductivity reconstructions with heavier LP filter. Data are collected using Siemens Tim Trio 3T scanner.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5098