5097

Error Analysis of Helmholtz-based MR-Electrical Properties Tomography

Stefano Mandija¹, Alessandro Sbrizzi¹, Ulrich Katscher², Peter R. Luijten¹, and Cornelis A.C. van den Berg¹

¹Center for Image Sciences, UMC Utrecht, Utrecht, Netherlands, ²Philips Research Laboratories, Hamburg, Germany

Synopsis

The numerical error arising from the computation of spatial derivatives using finite difference kernels is investigated for Helmholtz-based MR-Electrical-Properties-Tomography conductivity reconstructions. We show that this numerical error is one major cause of limited accuracy in Helmholtz-based MR-EPT reconstructions, even if mitigation strategies such as Gibbs ringing correction and Gaussian apodization in k-space are adopted. Ultimately, large derivative kernels lead to more noise-robust conductivity reconstructions, at the cost of more spatially-extended boundary errors. If boundaries are not explicitly taken into account during reconstructions, the accuracy of MR-EPT is severely hampered, particularly for spatially convoluted tissues such as the human brain.

Introduction

MR-Electrical Properties Tomography (MR-EPT) aims to measure tissue electrical properties (EPs: conductivity σ, and permittivity ε) at RF frequencies (64-300 MHz) using MR-scanners¹. This technique has already been applied in in-vivo studies^2-5. However, the presented results show large variability in the reconstructed EPs values^6-9. Helmholtz-based MR-EPT reconstructions are performed by computing spatial derivatives of the complex transmit RF field (B₁⁺), i.e. by convolving the acquired MR images with finite difference (FD) derivative kernels^10,11. This derivative operation is very sensitive to spatial fluctuations caused by noise and Gibbs ringing (GR). Moreover, at tissue boundaries, FD kernels include voxels that belong to regions with different EPs. In this work, the error arising from the computation of spatial derivatives using finite difference kernels (FD error) has been investigated for Helmholtz-based MR-EPT conductivity reconstructions. It is also investigated whether mitigation strategies such as GR correction¹² and Gaussian apodization (GA) in k-space¹³ can be beneficial.

Methods

Standard MR-EPT conductivity reconstructions were performed according to¹:

$$σ(\mathbf{r})≈\frac{1}{μ_{0}ω}Im(\frac{\triangledown^2B_1^+(\mathbf{r})}{B_1^+(\mathbf{r})})≈\frac{1}{μ_{0}ω}Im(\frac{B_1^+(\mathbf{r})*K}{B_1^+(\mathbf{r})})$$

and phase-only conductivity reconstructions were performed according to¹:

$$σ(\mathbf{r})≈\frac{1}{μ_{0}ω}Im(\frac{\triangledown^2e^{iφ^+(\mathbf{r})}}{e^{iφ^+(\mathbf{r})}})≈\frac{1}{μ_{0}ω}Im(\frac{e^{iφ^+(\mathbf{r})}*K}{e^{iφ^+(\mathbf{r})}})$$

with φ⁺: B₁⁺ phase, K: 2^nd order FD kernel (K₃: 3×3×3 voxels, and K₇: 7×7×5 voxels)¹⁴, ω: frequency, and μ₀: vacuum permeability.

FDTD simulations were performed in Sim4Life (ZMT, Zurich) on a cylindrical model and on a human head model (Duke, Virtual Family) with piecewise constant EPs. Simulations were used to evaluate the accuracy of MR-EPT reconstructions, as they allow knowledge of the ground truth (i.e. input EPs values). We defined with V_RE<30% the percentage of voxels with relative error < 30%.

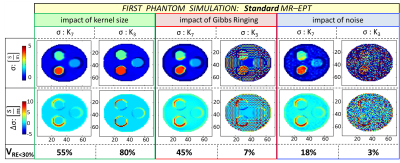
First phantom simulation: we evaluated the impact of FD kernel size, Gibbs ringing, and superimposed noise (B₁⁺ magnitude SNR = 30) on standard MR-EPT reconstructions.

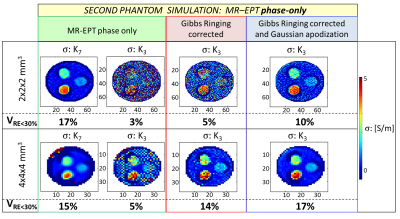
Second phantom simulation: we evaluated whether GR-correction¹² and k-space-GA¹³ improve the reconstruction accuracy (V_RE<30%) as a function of the voxel size. Phase-only conductivity reconstructions were performed to allow comparison with MR-measurements.

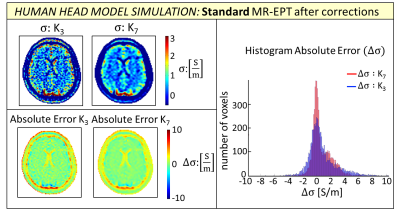
Human head model simulation: we evaluated the accuracy (V_RE<30%) of both standard and phase-only MR-EPT conductivity reconstructions as a function of SNR and FD kernel size, after the aforementioned mitigation strategies were applied.

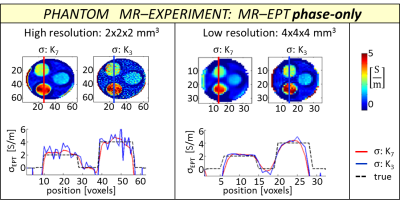
From MR-measurements (3T, Ingenia, Philips) on an agar-based phantom, phase-only conductivity reconstructions were performed, employing the transceive phase assumption¹⁴. Two single-slice, Spin-Echo phase maps acquired with opposite readout gradient polarities were combined to compute the RF phase maps used for phase-only conductivity reconstructions: TR/TE = 900/5 ms, field of view = 256×256 mm², voxel size = 2×2×2 mm³ and 4×4×4 mm³ for the high and low-resolution experiments, respectively.

Results and Discussion

Fig. 1 shows that MR-EPT conductivity reconstructions are accurate inside homogeneous regions for the noiseless case (absolute error ∆σ ≈ 0 S/m, V_RE<30% > 55%). However, given realistic conditions, the small FD kernel is highly sensitive to Gibbs ringing and noise, whereas the large, noise-robust FD kernel leads to extended boundary errors (V_RE<30% ≈ 3% for K₃, and 18% for K₇).

Fig. 2 shows that K₇ performs globally better than K₃ for realistic conditions, since it is more noise-robust. K-space-GA helps improving the accuracy for high resolution reconstructions, while the accuracy is improved by GR-correction for low resolution reconstructions. Still, V_RE<30% is not higher than 20% even after applying mitigation strategies.

Phase-only conductivity reconstructions from phantom MR-measurements after these mitigation strategies were applied (Fig. 3) confirm the results observed in the second phantom simulation.

In Fig. 4, standard MR-EPT reconstructions on a head model and absolute error maps are presented after GR-correction and k-space-GA. The impact of spatial fluctuations is reduced inside large homogeneous regions such as the WM if K₇ is used, compared to K₃ reconstructions. However, more boundary error propagation is introduced. This limits the reconstruction accuracy for spatially convoluted tissues such as the GM and the CSF.

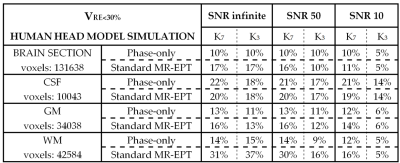
In Tab. 1, the reported V_RE<30% values for standard and phase-only MR-EPT conductivity reconstructions indicate that the global accuracy is generally low and does not substantially improve with increasing SNR levels. Ultimately, even for the WM, which is the largest homogeneous tissue in the brain, V_RE<30% is at most 37%.

Conclusions

The numerical error introduced by the computation of spatial derivatives using FD kernels is one of the major causes of limited accuracy in Helmholtz-based MR-EPT reconstructions, even if mitigation strategies are adopted. Increasing FD kernel size leads to more noise-robust reconstructions, at the cost of more extended boundary errors. If boundaries are not taken into account explicitly during reconstruction, the accuracy of MR-EPT is severely hampered, particularly for spatially convoluted tissues such as the human brain.

Acknowledgements

The authors would like to thank Janot P. Tokaya, Ettore F. Meliado and Astrid L.H.M.W. van Lier for constructive discussions.

References

1. Katscher U, van den Berg C a. T. Electric properties tomography: Biochemical, physical and technical background, evaluation and clinical applications. NMR Biomed. 2017: early view. doi: 10.1002/nbm.3729.

2. Shin J, Kim MJ, Lee J, Nam Y, Kim M, Choi N, Kim S, Kim D-H. Initial study on in vivo conductivity mapping of breast cancer using MRI. J. Magn. Reson. Imaging 2014:371–378. doi: 10.1002/jmri.24803.

3. Van Lier ALHMW, Hoogduin JM, Polders DL, Boer VO, Hendrikse J, Robe PA, Woerdeman PA, Lagendijk JJW, Luijten PR, van den Berg CAT. Electrical conductivity imaging of brain tumours. Proc. 19th Annu. Meet. ISMRM. Montréal, Québec, Canada 2011;19:4464.

4. Tha KK, Katscher U, Yamaguchi S, Stehning C, Terasaka S, Fujima N, Kudo K, Kazumata K, Yamamoto T, Van Cauteren M, Shirato H. Noninvasive electrical conductivity measurement by MRI: a test of its validity and the electrical conductivity characteristics of glioma. Eur Radiol. 2017 Jul 11. doi: 10.1007/s00330-017-4942-5

5. Balidemaj E, de Boer P, van Lier a LHMW, Remis RF, Stalpers LJ a, Westerveld GH, Nederveen a J, van den Berg C a T, Crezee J. In vivo electric conductivity of cervical cancer patients based on B1+ maps at 3T MRI. Phys. Med. Biol. 2016;61:1596–1607. doi: 10.1088/ 0031-9155/61/4/1596.

6. Kim D, Choi N, Gho S, Shin J, Liu C. Simultaneous Imaging of In-vivo Conductivity and Susceptibility. Magn. Reson. Med. 2014;71:1144–1150. doi: 10.1002/mrm.24759.

7. Lee J, Shin J, Kim D. MR-Based Conductivity Imaging Using Multiple Receiver Coils. Magn. Reson. Med. 2015. doi: 10.1002/mrm.25891.

8. Van Lier ALHMW, Raaijmakers A, Voigt T, Lagendijk JJW, Katscher U, Van Den Berg CAT. Electric properties tomography in the human brain at 1.5, 3, and 7 T: a comparison study. Magn. Reson. Med. 2014;71:354–363. doi: 10.1002/mrm.24637.

9. Gurler N, Ider YZ. Gradient-Based Electrical Conductivity Imaging Using MR Phase. Magn. Reson. Med. 2016;00:00–00. doi: 10.1002/mrm.26097.

10. Duan S, Xu C, Deng G, Wang J, Liu F, Xin SX. Quantitative analysis of the reconstruction errors of the currently popular algorithm of magnetic resonance electrical property tomography at the interfaces of adjacent tissues. NMR Biomed. 2016:744–750. doi: 10.1002/nbm.3522.

11. Lee S, Bulumulla S, Hancu I. Theoretical Investigation of Random Noise-Limited Signal-to-Noise Ratio in MR-Based Electrical Properties Tomography. IEEE Trans. Med. Imaging 2015;34:2220–2232.

12. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med. 2015; 76:1574–1581. doi: 10.1002/mrm.26054.

13. Mandija S, Sbrizzi A, van Lier ALHMW, Luijten PR, van den Berg CAT. Proc. 24th Sci. Meet. Int. Soc. Magn. Reson. Med. Singapore, 2016:2989.

14. van Lier ALHMW, Brunner DO, Pruessmann KP, Klomp DWJ, Luijten PR, Lagendijk JJW, Van Den Berg CAT. B1+ phase mapping at 7 T and its application for in vivo electrical conductivity mapping. Magn. Reson. Med. 2012;67:552–561. doi: 10.1002/mrm.22995.

Figures

Figure 1: First phantom simulation. Impact of two different FD kernel sizes (K₃: 3×3×3 voxels, del2 function in Matlab, and K₇: 7×7×5 voxels, appendix of reference 14), Gibbs Ringing and noise on standard MR-EPT conductivity reconstructions (first row). Absolute conductivity error maps are also shown (second row). The reported V_RE<30% values indicate the percentage of voxels with a relative error lower than 30%. The cylindrical phantom model had three inner compartments with different conductivities (1, 2, 4 S/m, respectively, and 0.1 S/m for the background).

Figure 2: Second phantom simulation. Phase-only conductivity reconstructions: Impact of FD kernel size (K₃ and K₇), Gibbs ringing correction and additional Gaussian apodization for a voxel size of 2×2×2 mm³ and 4×4×4 mm³. To consider the intrinsic increase in SNR in an MR-experiment due to a larger voxel size, the SNR was respectively 30 (high resolution reconstructions, first row) and 120 (low resolution reconstructions, second row). V_RE<30% values are also reported for each reconstruction.

Figure 3: Phantom MR-experiment at 3T. Phase-only conductivity reconstructions for a voxel size of 2×2×2 mm³, and 4×4×4 mm³. For both cases, reconstructions were performed after both GR-correction and k-space-GA were applied. The conductivity values of the three inner tubes and the background were the same as the one used for the simulation (1, 2, 4 S/m for the inner tubes, respectively, and 0.1 S/m for the background). The 2D version of the adopted FD kernels was used.

Figure 4: Human head model simulation. Standard MR-EPT conductivity reconstructions for two different kernel sizes (K₃ and K₇) performed after both GR-correction and k-space-GA were applied. Absolute error maps for both kernels and the histogram of the computed absolute errors are also shown. The input conductivity values in [S/m] were: 2.14 for the Cerebrospinal fluid (CSF), 0.34 for the white matter (WM), 0.58 for the gray matter (GM), 0.06 for the skull, and 0.54 for the skin.

Table 1: Human head model simulation: V_RE<30% for a whole 3D brain section (thickness: 7 cm), and for the only CSF, GM, and WM regions inside this section. Conductivity reconstructions were performed using standard MR-EPT and phase-only MR-EPT approaches, two different kernel sizes (K₇ and K₃) and different SNR levels (infinite, 50, and 10), after both Gibbs ringing correction and Gaussian apodization were applied.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5097