5094

Automated Seed Selection for Gradient-based Electrical Properties Tomography and Its in vivo Validation in the Brain

Yicun Wang¹, Pierre-Francois Van de Moortele², and Bin He^1,3

¹Department of Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, ²Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, ³Institute for Engineering in Medicine, University of Minnesota, Minneapolis, MN, United States

Synopsis

Electrical Properties Tomography (EPT) retrieves tissue electrical conductivity and permittivity at Larmor frequency which potentially provides diagnostic information and facilitates subject-specific local SAR estimation. Gradient-based EPT (gEPT) significantly alleviates boundary artifact encountered by conventional EPT methods, yet its implementation requires subjective assignment of integration seed points. In this study, we developed an automated seed selection strategy based on locally calculated conductivity values, and evaluated the effect of seed number for human brain imaging. This new strategy was validated in eight healthy subjects to produce robust and accurate results, paving the path for an unbiased and fully-automated process for EP quantification.

Introduction

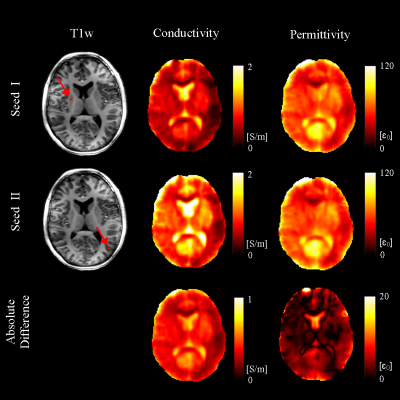
Electrical Properties Tomography employs radiofrequency $$$B_1$$$ field measured in MRI to non-invasively quantify tissue conductivity and permittivity, with great potentials for cancer diagnosis and realistic SAR estimation^1,2. Gradient-based EPT (gEPT) is a recently proposed technology that preserves correct EP contrast on tissue boundaries by explicitly reconstructing the spatial variation or “gradient” of tissue EPs, followed by its integration from an user-assigned seed point³. However, systematic reconstruction bias exists owing to the subjective assignment of seed points(Fig. 1). In this study, we propose a strategy to automatically select multiple distributed seed points based on locally calculated EP values. Imaging data from eight healthy subjects were used to validate the proposed approach.

Methods

Experiment Eight human subjects were recruited for a brain scan at Siemens 7T MRI using a 16 channel microstrip coil array. Relative complex $$$B_1^+$$$ from each channel was acquired by a series of GRE in the small-flip-angle regime, with calibration using Actual Flip-angle Imaging (AFI) of all channels transmitting in a static $$$B_1^+$$$ shim setting⁴. Proton density weighted relative complex $$$B_1^-$$$ was acquired using a long TR (TR=8s) GRE. Both $$$B_1$$$ maps were acquired as axial slices in a resolution of $$$1.5\times1.5\times3mm^3$$$.

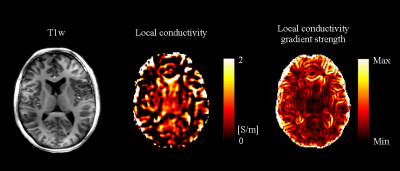
Image Reconstruction Proton density weighting $$$\rho$$$ in the measured $$$B_1^-$$$ was estimated and removed using $$$\rho\approx\frac{\sum_j|\rho B_{1,j}^-|}{\sum_k|B_{1,k}^+|}$$$, where $$$k$$$ and $$$j$$$ denote transmit and receive channels, respectively. Relative $$$B_1^+$$$ and $$$B_1^-$$$ were smoothed using a $$$5\times5\times3$$$ Gaussian low-pass filter with standard deviation of $$$1.2\times1.2\times0.8$$$, and their spatial gradient and Laplacian were taken with $$$5\times5\times3$$$ Savitzky-Golay filters. Relative $$$B_1^+$$$ from all 16 channels were concatenated to produce a linear equation system, which was solved pixel by pixel to yield absolute $$$B_1^+$$$ phase gradient $$$\frac{\partial{\phi^+}}{\partial{x}}$$$ and $$$\frac{\partial{\phi^+}}{\partial{y}}$$$, as well as a Wirtinger derivative $$$g_+=\frac{\partial{ln\epsilon_c}}{\partial{x}}+i\frac{\partial{ln\epsilon_c}}{\partial{y}}$$$, where $$$\epsilon_c$$$ is the complex electrical property comprised of conductivity and permittivity. Similarly, relative $$$B_1^-$$$ from all 16 channels were concatenated to yield $$$\frac{\partial{\phi^-}}{\partial{x}}$$$, $$$\frac{\partial{\phi^-}}{\partial{y}}$$$, and $$$g_-=\frac{\partial{ln\epsilon_c}}{\partial{x}}-i\frac{\partial{ln\epsilon_c}}{\partial{y}}$$$. Local EP values were calculated by Helmholtz equation assuming piece-wise homogeneity $$$\epsilon_{c,local}=\frac{-\nabla^2B_1^+}{\omega^2\mu_0B_1^+}$$$ with measured $$$|B_1^+|$$$ and calculated $$$\frac{\partial{\phi^+}}{\partial{x}}$$$ and $$$\frac{\partial{\phi^+}}{\partial{y}}$$$ in the previous step. Brain voxels with local EP values falling in the range of $$$0\leq\sigma\leq3S/m$$$ and $$$0\leq\epsilon\leq100\epsilon_0$$$ were sorted in ascending order based on the spatial gradient strength of local conductivity. The top N voxels with the smallest local conductivity gradient magnitude were chosen as seed points, since they are expected to be less affected by the large oscillations near tissue boundaries. The chosen seeds were weighted equally during the final integration of the EP gradient.

Results

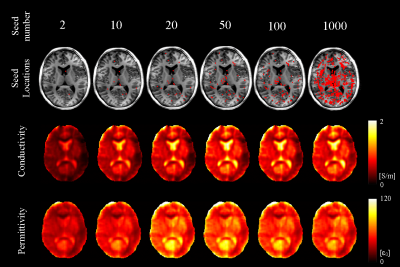
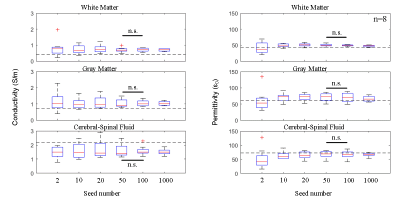
Local conductivity calculated by the Helmholtz equation and its gradient strength are shown in Fig 2. The top 2, 10, 20, 50, 100 and 1000 seeds were chosen, and their corresponding EP reconstruction results are shown in Fig 3. Both conductivity and permittivity seem to be underestimated for this subject when the number of seeds is smaller than 20. The reconstruction results stabilize when more than 20 seeds were chosen, and the stability remains up to as large as 1000 seeds. This feature is also observed in the aggregated results across all subjects (Fig. 4). The inter-subject variation is large when a small number of seed were chosen, and decreases as the seed number increases. There is no statistically significant difference between the results with 50 and 100 seeds.

Discussion

In this study, we demonstrated that EP values calculated by local Helmholtz equation could inform gEPT reconstruction, and we showed that a large number of seeds help to stabilize the results. This is potentially due to the reduced weighting on erroneously chosen seeds when the seed number is large. To further reduce reconstruction bias by the symmetry assumption made by gEPT, it is desirable to test this algorithm with only $$$g_+$$$ data derived from $$$B_1^+$$$ only.^5,6 In addition, we observed consistent EP values of brain tissues in our cohort of human subjects, which are close yet not equal to the values reported in the widely referenced work by Gabriel et al^7,8. This discrepancy is potentially due to the in vivo nature of MREPT versus ex vivo probe measurement, fitting errors to the Cole-Cole dispersion model, and intrinsic EP heterogeneity among subjects due to age or body condition⁹.

Conclusion

A novel strategy to automatically choose integration seeds for gEPT brain imaging has been proposed and validated in eight subjects. The reconstructed conductivity and permittivity are consistent and close to the literature reported values. Enhanced robustness and less variability are observed compared to the subjective single-seed method. This technology holds promise to facilitate an objective and fully-automated EPT approach for in vivo imaging of human brain.

Acknowledgements

NIH R21 EB017069, R01 AT009263, R01 EB021027, R01 NS096761, RF1 MH114233, P30 NS076408, P41EB015894 and S10RR026783, and WM KECK Foundation.

References

1. Liu J, Wang Y, Katscher U, He B. Electrical properties tomography based on B1 maps in MRI: principles, applications, and challenges. IEEE Trans. Biomed. Eng. 2017;64:2515–2530.

2. Katscher U, van den Berg CAT. Electric properties tomography: biochemical, physical and technical background, evaluation and clinical applications. NMR Biomed. 2017;30:e3729.

3. Liu J, Zhang X, Schmitter S, Van de Moortele P-F, He B. Gradient-based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn. Reson. Med. 2015;74:634–646.

4. Van de Moortele PF, Snyder C, DelaBarre L, Adriany G, Vaughan JT, Ugurbil K. Calibration Tools for RF Shim at Very High Field with Multiple Element RF Coils: from Ultra Fast Local Relative Phase to Absolute Magnitude B1+ Mapping. In: Proc. Intl. Soc. Mag. Reson. Med. 15, Berlin, Germany; 2007, p. 1676.

5. Liu J, Zhang X, Wang Y, Van de Moortele P-F, He B. Local Electrical Properties Tomography With Global Regularization By Gradient. In: Proc. Intl. Soc. Mag. Reson. Med. 23, Toronto, Canada; 2015, p. 1855.

6. Wang Y, Van de Moortele P-F, He B. CONtrast Conformed Electrical Properties Tomography (CONCEPT) Based on Multi-Channel Transmission. In: Proc. Intl. Soc. Mag. Reson. Med. 25, Honolulu, USA; 2017, p. 3640.

7. Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996;41:2251–2269.

8. Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996;41:2271-2293.

9. Peyman A, Rezazadeh AA, Gabriel C. Changes in the dielectric properties of rat tissue as a function of age at microwave frequencies. Phys. Med. Biol. 2001;46:1617–1629.

Figures

Figure 1. Discrepancies in gEPT reconstruction results due to different choices of seed point. Location of seed point is labeled as a red dot (pointed by red arrow) on T1 weighted (T1w) image. Seed I was located in the Globus Pallidus and seed II was located in the cortex. The EP values of gray matter at 298MHz were assigned in both cases.

Figure 2. T1w image, calculated local conductivity distribution and its gradient strength.

Figure 3. Reconstructed conductivity and permittivity using EP gradient and different numbers of automatically selected seeds. The reconstruction results become stable for seed number >20.

Figure 4. Box plot of aggregated results from one similar axial brain slice of eight human subjects. Supervised thresholding of T1w image was used to segment the brain into three compartments: gray matter, white matter and cerebral-spinal fluid. Black dashed line labels the literature reported EP values of the corresponding brain tissue at 298MHz from Gabriel et al. 1996⁸. Paired t-test was performed for all brain tissues with 50 and 100 seeds. n.s. not significant.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5094