5092
An Explicit Method for MR-Based Electrical Properties Reconstruction Free from Their Boundary Values1The University of Tokyo, Tokyo, Japan
Synopsis
This paper presents a new explicit reconstruction method for Magnetic Resonance Electrical Properties Tomography (MREPT) in a circular region of interest (ROI) that does not require EP values on the boundary of the ROI. Starting from the complex form of Maxwell's equations, we solved the D-bar equation of the electric field with the Neumann boundary condition. The proposed method reconstructs EPs successfully without giving any knowledge of EP values on the boundary of the ROI. To extend the method to, for example, a rectangular ROI, is our future work.
Introduction
Magnetic Resonance Electrical Properties Tomography (MREPT) is an imaging technique that reconstructs the electrical properties (EPs), that is, the conductivity and the permittivity, of biological tissues from internal magnetic field data measured by MRI1,2. Because some malignant tissues show significantly different EP values from normal ones, EP maps give useful information for the diagnosis of cancer. We previously proposed an explicit reconstruction method for MREPT based on the D-bar equation of the electric field3. In this method, the distributions of EPs on the boundary of the region of interest (ROI) must be given as a Dirichlet boundary condition of the D-bar equation, which is difficult in practical situation, though. Thus, in this paper, we propose a new explicit reconstruction method for MREPT in a circular ROI that does not require the EP values on the boundary of the ROI.Methods
The electromagnetic fields in the MR radio frequency coil is governed by time-harmonic Maxwell's equations. By a 2D approximation, we can derive the following complex partial differential equations: $$\bar{\partial} E_{z} = \omega \mu_{0} H^{+}, \quad 4\partial H^{+} = -\omega \kappa E_{z},$$ where $$$\partial \equiv (\partial_{x} - i\partial_{y})/2$$$ and $$$\bar{\partial} \equiv (\partial_{x} + i\partial_{y})/2$$$ are complex differential operators and $$$H^{+}$$$ is the positively rotating component of the magnetic filed measured by MR scanner. $$$\kappa$$$ is defined by $$$\kappa \equiv \epsilon - i\sigma/\omega$$$ where $$$\epsilon$$$ and $$$\sigma$$$ are the permittivity and the conductivity, respectively. The detailed derivation is written in [3]. In our previous method, the D-bar equation was solved using the generalized Cauchy's integral formula with the Dirichlet boundary condition, whereas in the proposed method, we solve the equation from the Neumann boundary condition. For a circular region $$$D$$$ with a radius $$$a$$$, applying the Neumann-type integral formula4 to $$$E_{z}$$$ yields $$E_{z}(\zeta_{0}) = -\frac{1}{2\pi i} \oint_{\partial D} \frac{a\log{(1-\zeta_{0}/\zeta)}}{\zeta-\zeta_{0}} (\partial_{n}E_{z} - \frac{\bar{\zeta}}{a} \bar{\partial} E_{z}) d\zeta -\frac{1}{\pi} \iint_{D} \frac{\zeta_{0} \bar{\partial} E_{z}}{\zeta(\zeta-\zeta_{0})} d\xi d\eta + c, \quad \zeta_{0} \in D.$$ In MREPT problem, the normal derivative of $$$E_{z}$$$ on $$$\partial D$$$ is represented as $$$\partial_{n} E_{z} = (\zeta/a) \partial E_{z} + (\bar{\zeta}/a) \bar{\partial} E_{z} = -(\zeta/a)\omega \mu_{0} H^{-} + (\bar{\zeta}/a) \omega \mu_{0} H^{+} \simeq (\bar{\zeta}/a) \omega \mu_{0} H^{+}$$$ by Ampere's law. Here, we used the assumption5 that $$$|H^{-}| \ll |H^{+}|$$$ and its validity is discussed below. Therefore, the explicit representation of $$$E_{z}$$$ is derived as follows: $$E_{z}(\zeta_{0}) = -\frac{1}{\pi} \iint_{D} \frac{\zeta_{0} \omega \mu_{0} H^{+}}{\zeta(\zeta-\zeta_{0})} d\xi d\eta + c.$$ This formula contains only the measurable quantity $$$H^{+}$$$ and $$$\kappa$$$ on the boundary $$$\partial D$$$ is not needed. Finally, $$$\kappa$$$ is directly calculated by the relation that $$$\kappa(\zeta_{0}) = -4\partial H^{+}/(\omega E_{z}).$$$ Note that the constant $$$c$$$ can be determined by the fact that $$$E_{z}$$$ is zero at the point where $$$\partial H^{+}$$$ is zero.
We evaluated the proposed method by a numerical simulation using a finite element method simulator, COMSOL Multiphysics (COMSOL) and by a phantom experiment using 3 T MR scanner (Siemens, Magnetom Prisma). We compare the proposed method with our previous method. For the previous method, we gave a constant boundary EP values as the Dirichlet boundary condition.
Results
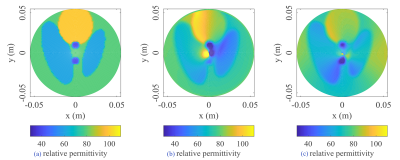
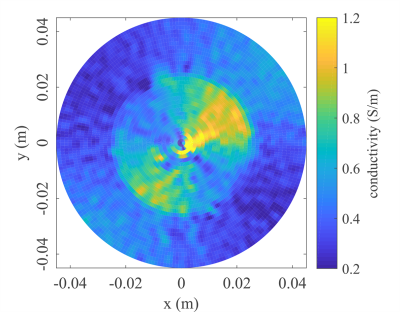
Figure 2 shows the reconstruction results of the relative permittivity of the simulation model. In the previous method, a severe artifact is observed around the central region. This error is caused because the boundary EP values are actually not constant. On the other hand, the proposed method correctly reconstructs the relative permittivity including the central region without giving boundary EP values. As shown in Fig. 4, the proposed method also successfully reconstructs the conductivity for the experimental phantom.Discussion
While the proposed method successfully reconstructed the relative permittivity for the simulation model, some additional deviations are observed near the boundary. This deviation is mainly due to the assumption that $$$|H^{-}| \ll |H^{+}|$$$ and to correct this term by calculating $$$H^{-}$$$ from $$$E_{z}$$$ obtained by the proposed method as an initial guess will improve the reconstruction results.
Although the proposed method is restricted to a circular ROI, it can reconstruct EPs without giving any information about EP values on the boundary of the ROI, and thus improve the applicability of MREPT in practical situations.
Conclusion
This paper presented a new explicit reconstruction method for MREPT in a circular ROI that does not require EP values on the boundary of the ROI. Starting from the complex form of Maxwell's equations, we solved the D-bar equation of the electric field with the Neumann boundary condition. The proposed method reconstructs EPs successfully without giving any knowledge of EP values on the boundary. To extend the method to, for example, a rectangular ROI, is future work.Acknowledgements
We are grateful to Mr. Katsutoshi Murata, Siemens Healthcare K.K., for his invaluable support in manipulating the MR scanner.
This work was supported by JSPS KAKENHI Grant Number JP26108003.
References
1. Haacke E, Petropoulos L, Nilges E, and Wu D. Extraction of conductivity and permittivity using magnetic resonance imaging. Phys. Med. Biol. 1991;36(6):723 - 734.
2. Katscher U, Kim D, Seo J. Recent progress and future challenges in MR electric properties tomography. Compt. Math. Methods Med. 2013;2013:1 - 11.
3. Nara T, Furuichi T, Fushimi M. An explicit reconstruction method for magnetic resonance electrical property tomography base on the generalized Cauchy formula. Inverse Problems. 2017;33:105005.
4. Begehr H. Boundary value problems in complex analysis I. Bol. Asoc. Mat. Venez. 2005;XII(1):65 - 85.
5. Katscher U, Voigt T, Findeklee C, et al. Determination of electric conductivity and local SAR via $$${B}_{1}$$$ mapping. IEEE Trans. Med. Imag. 2009;28(9):1365 - 1374.
Figures