5064

Modeling skeletal muscle perfusion through application of the continuous time random walk model to diffusion-weighted images
David Reiter1,2, Fatemeh Adelnia2, Donnie Cameron3, Christopher Bergeron2, Richard G. Spencer2, and Luigi Ferrucci2

1Radiology and Imaging Sciences, Emory University, Atlanta, GA, United States, 2National Institute on Aging, Baltimore, MD, United States, 3Clinical Magnetic Resonance Physics, University of East Anglia, Norwich, United Kingdom

Synopsis

The continuous time random walk (CTRW) model provides a flexible framework for representing complex diffusive processes, allowing for smooth interpolation between sub- and super-diffusion. This work presents supporting arguments for the application of the CTRW model to the measurement of skeletal muscle perfusion. We present model fit parameters from DW images of human skeletal muscle and compare estimates of intravascular volume fraction with previously reported values obtained using intravital microscopy.

INTRODUCTION:

The development of reliable and feasible approaches for mapping tissue microvasculature is an active area of research. Models have been developed that use diffusion-weighted (DW) images for mapping attributes of tissue microvasculature such as microvascular pool size1, architecture2, and function3,4. These models simplify the characterization of the vascular space within a given voxel to be represented by a single pseudo-diffusion coefficient. The most widely accepted approach to such quantification is the intravoxel incoherent motion (IVIM) model1. This bi-component model does not closely resemble the broad distribution of microvascular blood flow observed in vivo; for example, observations using intravital microscopy in skeletal muscle and brain tissue reveal a broad distribution of flow velocities in capillaries that spanned a tenfold range with a skew towards greater velocities5. A possible alternative to fit these data is the continuous time random walk (CTRW) model which may be better-suited for representing such broad heavy-tailed distributions, and has recently been suggested as a potential model for tissue perfusion6. In this study, we provide supporting arguments for the application of the CTRW model to the measurement of skeletal muscle perfusion. We present model fit parameters from DW images of human skeletal muscle and compare estimates of intravascular volume fraction (IVF) with previously reported intravital microscopy measurements.

MATERIALS & METHODS:

Theory: The CTRW model6,7 uses fractional-order partial derivatives as operators for describing the diffusion propagator P(x,t):

∂αP(x,t)/∂tα = Dα,β·∂βP(x,t)/∂xβ, [1]

where 0<α≤1 and 1<β≤2 represent the order of the fractional derivatives in time and space and are related to the waiting time and jump length probability distributions, respectively. As α and β deviate from 1 and 2, respectively, these distributions become heavy tailed, representing a greater likelihood of longer waiting times and jump lengths. The mean squared displacement can be related to these operators:

<[x(t) - x(0)]2>∝t2α/β , [2]

and illustrates how different combinations of α and β can yield either sub-diffusive (2α/β<1) or super-diffusive (2α/β>1) behavior7. The characteristic function of the diffusion propagator can be formulated by solving the fractional partial differential equation in Eq. 1:

p(q,t) = Eα(-Dα,β|q|βtα), [3]

where is the generalized diffusion coefficient, with units mmβ/sα, and Eα is the Mittag-Leffler function, defined as:

Eα(z)=∑∞k=0 zk/Γ(αk+1). [4]

The Γ function represents a generalization of the factorial function for real numbers and thus this definition encompasses the power expansion of the exponential function for α=1. A compact form of this expression has been derived in terms of diffusion-weighting value b, and for small values of b, can be expressed using the stretched exponential function6:

p(b)=exp(-(bD)β/2), [5]

where D is equivalent to diffusivity with units mm2/s. We therefore focus on the influence of β in Eq. 5 on diffusion properties suggesting its use as a marker of perfusion. Support for this interpretation is provided using a random walk simulation and experimental data. Data Acquisition: Images were obtained from 4 healthy volunteers using a 3T Philips Achieva MRI system with a 20cm 2-channel surface coil (SENSE Flex-L, Philips, Best, The Netherlands). Axial single-slice mid-thigh DW images were acquired using a spin echo sequence with triple-fat suppression, previously described8, with the following acquisition parameters: TE/TR=46/3000ms, b-values=0, 3, 7, 10, 15, 20, 25, 30, 40, 50, 70, 100, 200, 400, 600, and 800s/mm2, slice thickness=22mm, FOV=256mm×225mm , voxel size=2.6×2.6mm2.

RESULTS AND DISCUSSION:

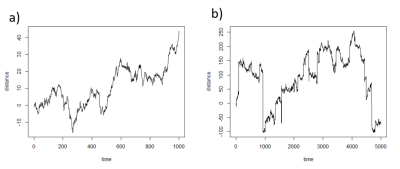
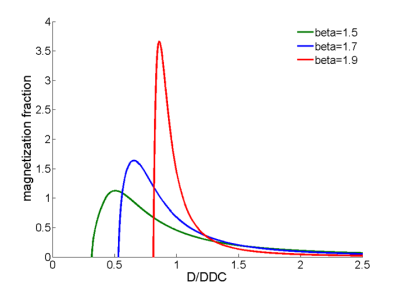
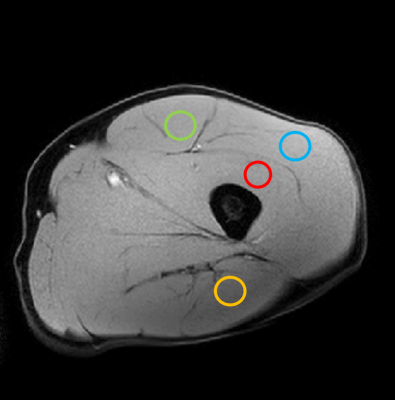
Figure 1 shows simulations from a one-dimensional random walk process illustrating the increased probability of longer jump lengths when β<2 compared with Brownian motion. Figure 2 shows the distribution of diffusivities produced by the stretched exponential function, which is skewed towards larger values with increased deviation of β from a value of 2; note for β=2, the distribution collapses to a single exponential value. Thus, the interpretation of β is that smaller values result in a larger relative volume fraction of intravascular space. Figure 3 shows select ROIs from select muscle groups reported in Table 1. Integration of model fit distributions (Figure 2) using values above a pseudo-diffusion cutoff defining the intravascular compartment11 produces estimates of IVF similar to previously reported values derived from intravital microscopy studies (e.g. 330 capillaries/mm2 with mean diameter of 5µm results in IVF of 0.0065)5,12.

CONCLUSION:

DW images from skeletal muscle contain information from a mixture of molecular motions arising from intravascular and extravascular compartments. The diffusivities within these compartments are expected to span a broad distribution of values, as has been observed from direct intravital microscopy of capillaries5,12 and imaging studies11. The CTRW model captures broad and skewed distributions of diffusivities providing a potential alternative for characterizing perfusion.

Acknowledgements

This research was supported in part by the Intramural Research Program of the NIH, National Institute on Aging.

References

1. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988; 168:497–505.

2. Karampinos D.C., King K.F., Sutton B.P., Georgiadis J.G., Intravoxel Partially Coherent Motion Technique: Characterization of the Anisotropy of Skeletal Muscle Microvasculature. JMRI. 2010; 31:942-953.

3. Filli L., Boss A., Wurnig M.C., Kenkel D., Andreisek G., Guggenberger R., Dynamic intravoxel incoherent motion imaging of skeletal muscle at rest and after exercise. NMR in Biomed. 2015; 28:240-246.

4. Nguyen A., Ledoux J-B., Omoumi P., Becce F., Forget J., Federau C., Applications of intravoxel incoherent motion perfusion imaging to shoulder muscles after a lift-off test of varying duration. NMR in Biomed. 2016; 29:66-73.

5. Ivanov K.P., Kalinina M.K., Levkovich Y.I., Blood flow velocity in capillaries of brain and muscles and its physiological significance. Microvascular Research. 1981; 22:143-155.

6. Ingo C., Sui Y., Chen Y., et al., Parsimonious continuous time random walk models and kurtosis for diffusion in magnetic resonance of biological tissue. Front. Phys. 2015; 3(11):1-11.

7. Metzler R., Klafter J., The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physical Reports. 2000; 338:1-77.

8. Cameron D., Reiter D.A., Bouhrara M., Fishbein K.W., Choi S., Bergeron C.M., Spencer R.G., Ferrucci L., Improved determination of anomalous diffusion parameters in human skeletal muscle using fat suppression. Proceedings of the ISMRM 24th Annual Meeting, 2016 #4243.

9. Meerschaert M.M., Sikorskii A., Stochastic models for fractional calculus. Vol. 43. Berlin: De Gruyter 2012.

10. Berberan-Santos MN., Valeur B., Luminescence decays with underlying distributions: general properties analysis with mathematical functions. J. Lumin. 2007; 126:263-272.

11. Zhang X., Ingo C., Teeuwisse W.M., Chen Z., van Osch M.J.P., Comparison of perfusion signal acquired by arterial spin labeling-prepared intravoxel incoherent motion (IVIM) MRI and conventional IVIM MRI to unravel the origin of the IVIM signal. Mag Res Med. 2017; DOI 10.1002/mrm.26723.

12. Honig C.R., Odoroff C.L., Frierson J.L. Capillary recruitment in exercise: rate, extent, uniformity, and relation to blood flow. Am. J. Physiol. 1980; 238:H31-42.

Figures

FIGURE 1. Simulation of a one-dimensional random walk process where β = 2 represents Brownian motion (a) and β = 1.6 illustrates the tendency towards greater jump lengths with smaller values of β (b). Simulation using R language was adapted from code provided in reference 9.

FIGURE 2. Representative distributions of diffusivities of the stretched exponential for β ranging from 1.5 to 1.9. This illustrates how greater deviations of β result in a heavy tailed distribution of diffusivities skewed towards more rapid diffusion values. Distributions were calculated based on work described in reference 10.

FIGURE 3. Reference Dixon water image showing select regions of interest used to calculate CTRW model parameters from diffusion weighted images: rectus femoris (green), vastus lateralis (blue), vastus intermedius (red), and biceps femoris (orange). Model fit values are reported in Table 1.

TABLE 1. CTRW model fit parameters obtained using region-of-interest (ROI) analysis with intravascular volume fraction (IVF) calculated through integration of model fit distributions using values above a pseudo-diffusion cutoff defining the intravascular compartment based on reference 11. IVF values are corrected for T1 and T2 differences between muscle and blood. Values are reported as mean (standard deviation) from ROIs shown in Figure 3 in four healthy volunteers.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5064