5063

Combined accelerated 4D Phase Contrast and 3D Diffusion Tensor Imaging reveals a complex relation between strain and muscle architecture in contracting leg muscles

Valentina Mazzoli^1,2,3, Martijn Froeling⁴, Lukas M Gottwald¹, Nico Verdonschot³, Melissa T Hooijmans¹, Aart J Nederveen¹, and Gustav J Strijkers^2,5

¹Department of Radiology, Academic Medical Center, Amsterdam, Netherlands, ²Biomedical NMR, Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, ³Orthopaedic Research Laboratory, Radboud UMC, Nijmegen, Netherlands, ⁴Department of Radiology, University Medical Center Utrecht, Utrecht, Netherlands, ⁵Biomedical Engineering and Physics, Academic Medical Center, Amsterdam, Netherlands

Synopsis

Skeletal muscles are geometrically complex 3D structures, and cannot be fully characterized by 2D imaging. Therefore, a complete understanding of mechanisms of force transmission and strain development in relation to muscle architecture during contraction requires a 3D approach. We measured strain rate in the lower leg using a 4D accelerated Phase Contrast protocol and 3D muscle architecture with DTI. Our 3D strain rate data revealed a planar pattern, with one negative and one positive strain rate eigenvalue. Strain rate data combined with 3D muscle architecture, suggested a complex and heterogeneous behavior of strain development during muscle contraction.

Introduction

Mathematical models of skeletal muscles have contributed to our understanding of the musculoskeletal system and were used to optimize surgical treatment (1–3). However, due to lack of subject-specific input, these models often rely on considerable simplifications and assumptions. For instance, it is often assumed that muscles shorten uniformly along their longitudinal axis, while evidence exists for more complex contraction patterns and non-collinear alignment of the direction of shortening with the muscle fiber direction (4,5). Furthermore, differences in deformation patterns were observed between deep and superficial muscles (4) and between proximal and distal locations (5,6). To reveal these highly complex patterns in muscle contraction and deformation, 3D imaging of contracting muscles and fiber architecture is a necessity.

The aim of this study was to quantify 3D strain rates in the lower leg musculature using Phase Contrast (PC) MRI and relate local strain rate patterns to 3D muscle architecture, obtained from DTI.

Methods

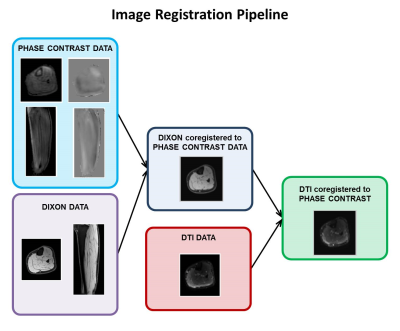
The right lower legs of five healthy volunteers were scanned using a 3T Philips Ingenia scanner. We acquired an anatomical mDixon and a DTI scan with the foot in dorsiflexed position. Subsequently, the subjects were instructed to perform active foot dorsi/plantarflexion (f=0.5 Hz) and an accelerated PC protocol was used to retrieve velocity information in skeletal muscles during contraction. All scans were acquired sagittally with the following scan parameters: FOV = 400 x 400 x 150 mm³, voxel sixe 1 x 1 x 1 mm³ (mDixon), 2.78 x 2.78 x 3 mm³ (DTI) and 1.79 x 1.79 x 5 mm³ (PC). For the DTI scan 3 b₀ and 12 diffusion weighted images (b=400 s/mm²) were acquired. For the PC scan, 3D velocity was measured with VENC=12 cm/s at 12 time points during the motion cycle. Scan time for the PC scan was 2.46 minutes, corresponding to 83 repetitions of the motion task. PC data was acquired by undersampling k-space based on a variable-density Poisson disc pattern. The undersampled data was reconstructed using a Compressed Sensing pipeline (7) implemented using the BART toolbox (8). The processing pipeline used to align PC and DTI data is illustrated in Figure 1. After image registration, the strain rate and the diffusion tensor were calculated from the PC and DTI data, respectively. The two tensors were subsequently diagonalized to obtain the principal strain rate eigensystem (local 3D contraction and expansion) and the principal directions of diffusion (local 3D fiber architecture).

Results

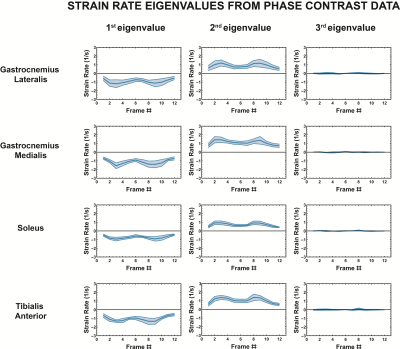
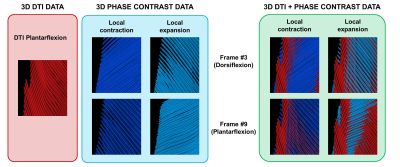
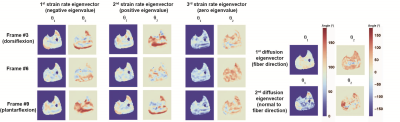
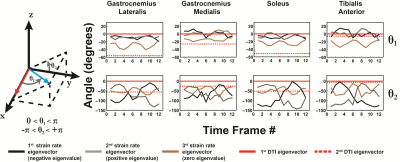
The strain rate tensor consistently resulted in one negative (local contraction, 1^st eigenvalue), one positive (local expansion, 2^nd eigenvalue) and one zero eigenvalue (3^rd eigenvalue) (Figure 2). Tracking of the eigenvectors of strain rate and diffusion showed that during active contraction the principal direction of contraction is almost aligned to (but slightly deviates from) the local fiber direction (Figure 3). Figure 4 shows the time evolution of the strain rate eigenvectors in one representative volunteer during the dorsi/plantarflexion cycle with respect to the muscle fiber orientations (1^stand 2^nd DTI eigenvectors). Eigenvector directions are expressed in polar-coordinates. These maps suggest a complex and heterogeneous pattern of strain development in contracting and relaxing muscles. Furthermore, we found that the elevation angle θ₂ of the principal direction of contraction closely aligned to fiber angle during contraction (frames #3 for Tibialis Anterior and frame #9 for Gastrocnemius Lateralis, Gastrocnemius Medialis and Soleus), while deviations between local fiber direction and strain rate directions were observed for the azimuthal angle θ₁ (Figure 5).

Discussion & conclusion

This study was the first to measure combined 4D strain rates and 3D muscle architecture with full coverage in the lower leg musculature. Due to the full 3D nature of DTI and PC acquisitions, strain directions could be compared to the fiber architecture at the voxel level, without requiring any assumptions on the nature of fiber arrangement and strain rate behavior. Our data revealed a planar but complex pattern of strain development in all the investigated muscles, in agreement with previous studies (4). The combination of strain rates with 3D muscle architecture obtained from DTI showed a complex and spatially heterogeneous pattern of strain development. This emphasizes the need for 3D analysis of fiber architecture and strain mechanisms. Furthermore, we observed angular deviations of strain rate directions from the local fiber direction, suggesting shearing between muscle fibers (5).

Taken together, these results can be used to obtain more accurate models of skeletal musculature, which in turn can lead to a deeper understanding of movement abnormalities and optimization of treatment strategies in muscle recovery and to improve intervention approaches to reduce loss of force production in aging processes.

Acknowledgements

No acknowledgement found.

References

1 Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J. Biomech. 2005;38:657–665. doi: 10.1016/j.jbiomech.2004.04.009.

2 Blemker SS, Asakawa DS, Gold GE, Delp SL. Image-based musculoskeletal modeling: Applications, advances, and future opportunities. J. Magn. Reson. Imaging 2007;25:441–451. doi: 10.1002/jmri.20805.

3 Asakawa DS, Blemker SS, Gold GE, Delp SL, Asakawa DS. In vivo motion of the rectus femoris muscle after tendon transfer surgery. J. Biomech. 2002;35:1029–1037. doi: 10.1016/S0021-9290(02)00048-9.

4 Englund EK, Elder CP, Xu Q, Ding Z, Damon BM. Combined diffusion and strain tensor MRI reveals a heterogeneous, planar pattern of strain development during isometric muscle contraction. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2011;300:R1079–R1090. doi: 10.1152/ajpregu.00474.2010.

5 Sinha U, Malis V, Csapo R, Moghadasi A, Kinugasa R, Sinha S. Age-related differences in strain rate tensor of the medial gastrocnemius muscle during passive plantarflexion and active isometric contraction using velocity encoded MR imaging: Potential index of lateral force transmission. Magn. Reson. Med. 2015;73:1852–1863. doi: 10.1002/mrm.25312.

6 Finni T, Hodgson J a, Lai AM, Edgerton VR, Sinha S. Nonuniform strain of human soleus aponeurosis-tendon complex during submaximal voluntary contractions in vivo. J. Appl. Physiol. [Internet] 2003;95:829–37. doi: 10.1152/japplphysiol.00775.2002.

7 Gottwald et al, Compressed Sensing accelerated time-resolved 3D phase contrast MRI of the lower leg muscles during active dorsi- and plantarflexion, 0093, Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

8 Uecker, Martin, et al. "Berkeley advanced reconstruction toolbox." Proc. Intl. Soc. Mag. Reson. Med. 2015; Vol. 23.

9 Klein et al. Elastix: A toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 2010;29:196–205.

Figures

Image registration pipeline. The mDixon scan was first aligned to the magnitude images of the PC scan. The first time frame of the coregistered mDixon scan, corresponding to full plantarflexion, was used as a target for registration of DTI data. All image registration steps were implemented in Elastix (9). Prior to image registration to the mDixon target, the DTI data was denoised using a PCA (Principal Components Analysis)-based algorithm, and all diffusion-weighted scans were non-rigidly registered to b₀ images to correct for eddy currents-induced image distortions.

Time evolution of the three strain rate eigenvalues (1^st, 2^nd and 3^rd) for the Gastrocnemius Lateralis, Gastrocnemius Medialis, Soleus and Tibialis Anterior. The results are averaged over all the subjects (mean, thick line and standard deviation, thin lines). Two distinct negative and positive peaks are observed for the 1^st and 2^nd eigenvalues respectively in peak dorsiflexion (frame #3) and peak plantarflexion (frame #9). The 3^rdeigenvalue of the strain rate tensor was consistently nearly zero, suggesting a planar pattern of strain development. Our results are in agreement with the hypothesis of muscle volume incompressibility (1^st+2^nd+3^rd eigenvalue = 0).

Tracking of principal fiber direction obtained using DTI (red box) and 1^st and 2^nd principal strain directions (blue box) in a ROI in the Gastrocnemius Medialis muscle. During dorsiflexion the muscle is not actively contracting, and is observed to expand (lenghten) along the fiber direction and to contract along the cross section of the fiber. The reversed behavior is observed during plantarflexion, when the muscle is actively contracting along the main fiber direction. Overlay of the principal directions of strain with the DTI data show a deviations of the principal directions of expansion and contraction from the local fiber direction.

Maps of direction of strain rate eigenvectors in the transverse plane for one volunteer. The direction is expressed in terms of angular deviation from the transverse plane in polar coordinates (θ₁=azimuthal angle, θ₂=elevation angle). The maps show a complex pattern of strain direction evolution over time. The direction of the first (fiber direction) and second (normal to fiber direction) DTI eigenvectors are shown for comparison on the right.

Change in orientation with respect to local fiber direction over time for the 3 principal strain rate directions averaged over the 5 volunteers for the Gastrocnemius Lateralis, Gastrocnemius Medialis, Solues and Tibialis Anterior muscles. The elevation angle θ₂ of principal direction of contraction (black line) is seen to approach the principal direction of diffusion (red line) in dorsiflexion for the Tibialis Anterior muscle (dorsiflexor muscle), while it is seen to approach the principal direction of diffusion in the Gastrocnemius Lateralis, Gastrocnemius Medialis and Soleus (plantarflexor muscles) in plantarflexion. A reversed behavior is observed for the principal direction of expansion (gray line).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5063