Synopsis

Correlation time ($\tau_c$) is an intrinsic property of molecules that can be probed from $T_{1\rho}$ dispersion measurement. The aim of this study was to evaluate the effect of low and high spin-lock frequencies (SLFs) on $\tau_c$ fitting and to find the optimum SLFs set within the typical clinical range. One bovine and two human cartilage samples were scanned to obtain $T_{1\rho}$ dispersion with 22 SLFs between 10 to 2500 Hz. $\tau_c$ maps were obtained by fitting Lorentzian function to different subsets of $T_{1\rho}$ dispersion. Our results show that $\tau_c$ fitting is significantly affected by low SLFs compared to high SLFs.

Introduction

Methods

Samples

This study utilized cylindrical osteochondral plugs (diameter = 6mm) of patellar cartilage from bovine (one plug) and human cadavers obtained from donors (two plugs, one per knee).

MRI

MRI was performed at 9.4 T using a 19 mm quadrature RF volume transceiver and VnmrJ3.1 Varian/Agilent DirectDrive console. The samples were imaged at room temperature and relaxation time measurements were realized using a global preparation-block coupled to a single slice FSE readout (TR=5s, Echo spacing=5.5ms, ETL=8 with centric echo ordering, matrix=256x64 (bovine sample) or 256x80 (human samples), FOV=16x12.8mm (bovine sample) or 16x16mm (human samples) and 1mm slice thickness, yielding a resolution of 62.5µm along cartilage depth). A single imaging slice was positioned at the center of the specimen, perpendicular to the axis of specimen. The measurements included CW-$T_{1\rho}$ dispersion with 22 SLFs⁴ (10, 20, 30, 50, 75, 100, 125, 150, 200, 250, 300, 400, 500, 600, 700, 800, 1000, 1200, 1500, 1800, 2200, 2500 Hz) and five spinlock times (0, 24, 48, 96, 192 ms).

Data analysis

$T_{1\rho}$ maps were fitted pixel-wise using two-parametric mono-exponential function. $\tau_c$ maps were obtained by fitting a Lorentzian function⁵

$$\frac{1}{T_{1\rho}}=\frac{3A \tau_c}{1+4\omega_{SL}^{2}\tau_c^{2}}+B,$$

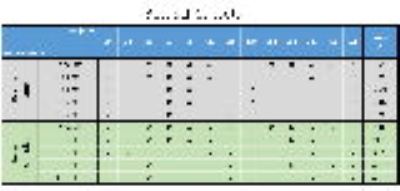
to $T_{1\rho}$ dispersion data, where ω_sl is the SLF, and A, B and $\tau_c$ are the fitting parameters. Outlier $\tau_c$ pixels, identified as those with values <1 ms in $T_{1\rho}$ maps at SLF of 0 Hz calculated from $\tau_c$ fitting function, were excluded from further analysis. Data analysis was performed using in-house developed MATLAB scripts and plugin functions for Aedes.⁶ To investigate the role of low and high SLFs on $\tau_c$ fitting, $\tau_c$ maps were fitted from different subsets of the $T_{1\rho}$ dispersion data. Influence of higher SLFs was explored by comparing datasets with different range of SLFs while fixing the lowest SLF (e.g. set1: 10-2500 Hz, set2: 10-2200 Hz,…). Similarly, low SLFs were studied by comparing datasets with different range of SLFs while fixing the highest SLF (e.g. set1: 10-2500 Hz, set2: 20-2500 Hz,...). Resulting $\tau_c$ maps were evaluated using mean difference and Pearson correlation coefficients with reference $\tau_c$ map (fitted using full-range dispersion, 10-2500 Hz). To find the optimum distribution of SLFs for $\tau_c$ fitting in frequency range 10-500 Hz, fitting was applied to data from all possible combinations for 4, 5, 6, 9 and 12 SLFs. Resulting $\tau_c$ maps were compared pixel-by-pixel with a reference $\tau_c$ map fitted using all 13 SLFs (10-500Hz). Percentage of absolute mean difference between each tested and reference $\tau_c$ map for each sample was calculated. Results of both human samples were averaged to form one dataset.

Results

After dropping more than two low-frequency SLFs from the fitting data, correlation of $\tau_c$ maps with the full-range $\tau_c$ reference map dropped from 0.63 to -0.10 (Figure 1-a and Figure 2-a). However, even after leaving out 13 high SLFs from fitting, $\tau_c$ map showed correlation of 0.59 compared to the full-range $\tau_c$ reference map (Figure 1-b and Figure 2-b). Best selections of 12, 9, 6, 5 and 4 SLFs resulted in $\tau_c$ maps with mean difference in the range of 1-10% in bovine sample, 5-46% in human samples, compared to the 13 SLFs reference map (Figure 3). $\tau_c$ maps fitted from best SLFs combinations showed similar laminar appearance to the reference $\tau_c$ map (Figures 4 and 5).

Discussion and Conclusion

Acknowledgements

Research funding from Jane and Aatos Erkko Foundation and support from the Academy of Finland (grants #285909 and #293970) are gratefully acknowledged. We also thank CSC-IT Center for Science in Espoo, Finland, for computing time.

References

1. Jones GP. Spin-lattice relaxation in the rotating frame: Weak-collision case. Physical Review. 1966;148(1):332.

2. Sepponen RE, Pohjonen JA, Sipponen JT, Tanttu JI. A method for $T_{1\rho}$ imaging. J Comput Assist Tomogr. 1985;9(6):1007-1011.

3. Wang P, Block J, Gore JC. Chemical exchange in knee cartilage assessed by $R_{1\rho}$ (1/$T_{1\rho}$) dispersion at 3T. Magn Reson Imaging. 2015;33(1):38-42.

4. Nissi MJ, Salo E, Tiitu V, et al. Multi‐parametric MRI characterization of enzymatically degraded articular cartilage. Journal of Orthopaedic Research. 2015.

5. Blicharska B, Peemoeller H, Witek M. Hydration water dynamics in biopolymers from NMR relaxation in the rotating frame. Journal of Magnetic Resonance. 2010;207(2):287-293.

6. Aedes – A graphical tool for analyzing medical images. http://aedes.uef.fi/

7. Mlynarik V, Szomolanyi P, Toffanin R, Vittur F, Trattnig S. Transverse relaxation mechanisms in articular cartilage. Journal of Magnetic Resonance. 2004;169(2):300-307.