5014
Dephasing and diffusion in blood vessel networks: an exact solution of the Bloch-Torrey-equation1E010 Radiology, German Cancer Research Center, Heidelberg, Germany, 2Neuroradiology, University Hospital Heidelberg, Heidelberg, Germany
Synopsis
The relaxation in blood vessel networks depends on susceptibility and diffusion effects around vessels. In 1994, Yablonskiy and Haacke developed a geometrical model of vessels and analyzed the gradient echo signal for negligible diffusion. Many approximative methods were developed generalizing this model in the limits of small and large diffusion effects. Important methods like vessel size or architectural imaging are based on these works. Here, we provide an exact solution of the Bloch-Torrey-equation in the model of Yablonskiy and Haacke for arbitrary diffusion effects that allows a validation of previously developed methods.
Introduction
An important model to describe MR signal decay for parallel, cylindrical vessel that are randomly distributed in a plane was introduced by Yablonskiy and Haacke1 in 1994, henceforth referred to as random vessel model (RVM). For negligible diffusion, they provided an analytical expression for the gradient-echo signal. Several further publications studied approximative methods generalizing the gradient-echo signal in the limiting cases of small and large diffusion effects2-4. Similarly, more simplistic tissue geometry models have been developed to analytically solve the Bloch-Torrey-equation5. Based on these works, important methods like vessel size imaging or vessel architectural imaging were brought forward3,6. Moreover, the obtained expressions for the gradient-echo signal are helpful for a better quantitative description of signal decay parameters including vessel size imaging, echo-time dependent QSM, quantitative perfusion measurements, etc. In this work, we provide the first exact closed-form solution of the Bloch-Torrey-equation in the RVM and discuss its potential for vessel size imaging.
Methods
In the RVM, the free induction decay $$$M(t)$$$ is related to the local magnetization $$$m(r,\phi,t)$$$ around a single vessel3: $$M(t) = \exp\left(-\eta\int\limits_{R}^{\infty}dr\,r\int\limits_{0}^{2\pi} d\phi [1-m(r,\phi,t)]\right)\,,$$ where $$$ \eta$$$ denotes the regional blood volume fraction. The local magnetization $$$m(r,\phi,t)=m_x(r,\phi,t)+{i}\,m_y(r,\phi,t)$$$ around a single vessel with radius $$$R$$$ is governed by the Bloch-Torrey-equation: $$\partial_t m(r,\phi,t) = [D\Delta-i\,\omega(r,\phi)] m(r,\phi,t)\,,$$ where $$$D$$$ denotes the diffusion coefficient and $$$\Delta$$$ the Laplace operator. The local Larmor frequency $$$\omega(r,\phi)$$$ depends on the susceptibility difference $$$\Delta\chi$$$ between blood and surrounding tissue: $$ \omega(r,\phi) = 2\pi \gamma B_0 \sin^2(\theta) \Delta\chi \frac{\cos(2\phi)}{r^2} R^2\,.$$ The angle $$$\theta$$$ is measured between vessel orientation and magnetic field $$$B_0$$$. We analytically solved the Bloch-Torrey equation to obtain the local magnetization. The free induction decay is obtained by solving the integral in Eq. (1). The obtained results are compared with random walk simulations; we simulate changes of the relaxation rates $$$R_2^{*}$$$ in vessel size imaging measurements and compare them to our analytical expressions.Results
The local
magnetization is obtained by solving the Bloch-Torrey-equation with a
separation ansatz. The angular eigenfunctions are Mathieu functions, the radial
eigenfunctions are obtained by a Laplace transform with respect to time and a
Neumann-Weber transform with respect to the radius $$$r$$$. Therefore, the
Neumann-Weber transform with complex indices has been analyzed. Finally, the
free induction decay is determined by solving the integral over the local
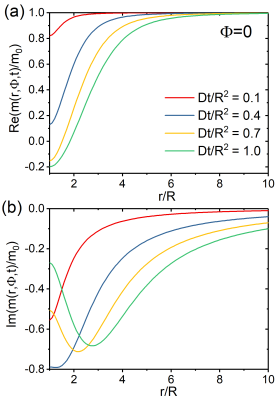
magnetization. The radial part of the local magnetization is shown in Fig. 1
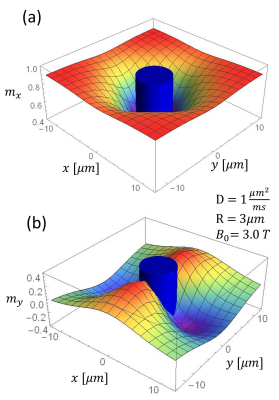
for different time points. It is only affected close to the surface of the vessel. Thus, the integral in Eq. (1) converges to a finite value. The local magnetization around a single vessel is shown in Fig. 2 for $$$TE=10\text{ms}$$$. The monoexponential relaxation rate $$$R_2^{*}$$$ is
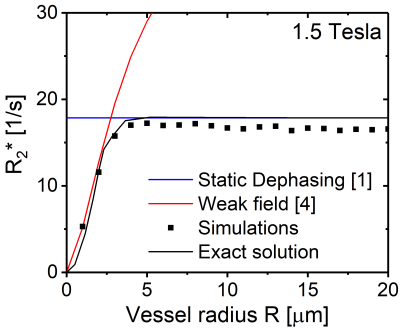
shown in Fig. 3 in dependence on the vessel radius $$$R$$$. For large vessel
radii, the relaxation rate $$$R_2^{*}$$$ agrees with the static dephasing limit
obtained by Yablonskiy and Haacke. For small vessel radii, the relaxation rate
decreases since the spin-bearing particles experience an averaged Larmor
frequency. In this limit, the weak field approximation is an appropriate approximation of the relaxation rate4. Our theoretical relaxation rate agrees very well with random walk
simulations for arbitrary vessel radii. Especially for small radii $$$R<5\mu m$$$, our model agrees much better than the usually applied static dephasing limit.
Discussion and Conclusion
In this work, we provide an exact solution of the Bloch-Torrey-equation around randomly distributed vessels. While this problem has extensively been analyzed over the last decades, so far, no exact solution of the Bloch-Torrey-equation could be found. For this purpose, we established a generalization of the Neumann-Weber transform for complex indices. The gradient echo relaxation rate agrees very well with random walk simulations. The results are relevant for vessel size imaging at 1.5 Tesla or 3.0 Tesla, where the static dephasing limit leads to an overestimation of the vessel radii for radii smaller than $$$5\mu m$$$. Our theoretical expression for $$$R_2^{*}$$$ can be used together with an appropriate model for $$$R_2$$$ to measure the vessel size index. At 1.5 Tesla, so far, the slow diffusion approximation3 and the weak field approximation4 provide good descriptions of the $$$R_2$$$ relaxation rate for $$$R>3.5\mu m$$$ and $$$R<2\mu m$$$, respectively. An exact description of the spin echo relaxation rate $$$R_2$$$ is mathematical challenging. However, a generalization of our approach for spin echo sequences might be possible.
In conclusion, we provide an exact description of the gradient echo signal around randomly distributed parallel vessels. The results agree very well with random walk simulations and a generalization of our approach might be able to describe the spin echo relaxation rate as well.
Acknowledgements
This work was supported by grants from the Deutsche Forschungsgemeinschaft (Contract Grant number: DFG ZI 1295/2-1 and DFG KU 3555/1-1). F. T. Kurz was supported by a postdoctoral fellowship from the medical faculty of Heidelberg University and the Hofmann-Klose foundation of Heidelberg University.References
1.D.A. Yablonskiy, E.M. Haacke. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn Reson Med. 1994;32:749-763.
2. W.R. Bauer, W. Nadler, M. Bock, L.R. Schad, C. Wacker, A. Hartlep, G. Ertl. The relationship between the BOLD-induced T2 and T2*:a theoretical approach for the vasculature of myocardium. Magn Reson Med. 1999;42:1004-1010.
3. V.G. Kiselev, S. Posse. Analytical model of susceptibility-induced MR signal dephasing: effect of diffusion in a microvascular network. Magn Reson Med. 1999;41:499-509.
4. J.H. Jensen, R. Chandra. NMR relaxation in tissues with weak magnetic inhomogeneities. Magn Reson Med. 2000;44:144-156.
5. C.H. Ziener, T. Kampf, G. Reents, H.-P. Schlemmer, W.R. Bauer. Spin dephasing in a magnetic dipole field. Phys Rev E. 2012;85: 051908.
6. K.E. Emblem, K. Mouridsen, A. Bjornerud, C.T. Farrar, D. Jennings, R.J.H. Borra, P.Y. Wen, P. Ivy, T.T. Batchelor, B.R. Rosen, R.K. Jain, A.G. Sorensen. Vessel architectural imaging identifies cancer patient responder to anti-angiogenic therapy. Nat Med. 2013;19:1178-1187.
Figures