Synopsis

Quantitative susceptibility mapping (QSM) is increasingly being applied to quantitative research on disease conditions including intracerebral hemorrhage, liver iron overload and bone mineral quantification. These applications require knowledge of the reproducibility of QSM of sources with high susceptibility, which has not been previously reported. Here, we investigate the agreement between QSM maps generated from gradient-echo scans acquired at multiple sites using multiple platforms.

Purpose

Quantitative susceptibility mapping (QSM) is increasingly being applied to quantitative research on disease conditions including intracerebral hemorrhage, liver iron overload and bone mineral quantification [1]. These new applications require knowledge of the reproducibility of QSM of sources with high susceptibility. Here, we investigate the agreement between QSM maps generated from gradient-echo scans acquired at multiple sites using multiple platforms.

Methods

Five identical phantoms were constructed and imaged at the primary study site, and four were shipped to four collaborating sites. Each phantom contained five balloons, each completely filled with a solution of gadolinium (Magnevist, Berlex Laboratories, Wayne, NJ) of varying concentrations (10, 5, 2.5, 1.25 or 0.625 mmol/L), and immersed in 1% agarose gel in a 16-ounce cylindrical plastic container. The gadolinium concentrations were selected to be representative of high susceptibility sources encountered in QSM applications, which can be as high as 3.2 ppm [2,3]. T2*-weighted acquisitions of the phantom, placed in a head coil, were performed on the scanners available at each site (Table 1) using the 3D multi-echo spoiled gradient-echo (SPGR) sequence available on the scanner and a range of imaging parameters specified in Table 2. The complex DICOM data was electronically transmitted to the coordination site for QSM reconstruction. A field map was obtained from the DICOM data using a non-linear voxel-wise fit with a correction to remove residual echo-to-echo phase inconsistencies in the readout direction when present. Quality guided field unwrapping and Laplacian Boundary Value (LBV) background field removal [1] were applied to obtain the local field map from which the QSM map was reconstructed using the MEDI+0 method [3], which minimized variation in the agarose gel medium of the phantom according to the expression:

$$\chi^\ast\ \ = argmin_\chi\ \ 1/2\ ‖w(e^{-if}-e^{-i(d*χ) } )‖_2^2+λ_1 ‖M_G ∇χ‖_1+λ_2 ‖M_{AGAROSE} (χ-\overline{χ_{AGAROSE}} )‖_2^2$$

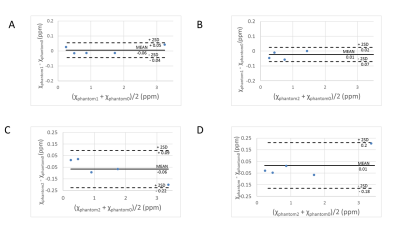
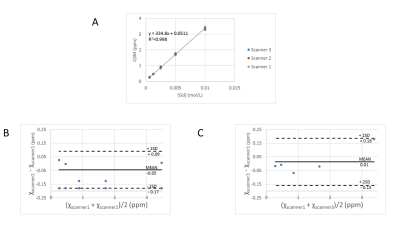
where $$$\chi$$$ is the susceptibility map, * is the convolution operation, w is noise weighting, f the measured local field, $$$\nabla$$$ the gradient operator, and $$$M_G$$$ a binary edge mask. The term, $$$\overline{χ_{AGAROSE}}$$$, penalizes susceptibility variation within the agarose gel medium, which can be isolated using a mask, $$$M_G$$$ , derived from the magnitude image, in a search for a solution with homogenous agarose susceptibility. The regularization values and were determined using L-curve plot analysis. The susceptibility in each balloon was estimated as the mean voxel value in a 60 $$$mm^3$$$ spherical region of interest (ROI) referenced to the mean voxel value in a large ROI drawn in the 1% agarose gel. The agreement between susceptibility estimates from different sites was evaluated using linear regression of QSM measurements against prepared gadolinium concentrations and Bland-Altman analysis to determine the 95% limits of agreement (average difference ± 2 × standard deviation of difference) for each pair of scans.

Results

Discussion

Conclusion

Acknowledgements

References