5000
Quantitative susceptibility mapping Accelerated Reconstruction Technique (QUART): A novel Split Bregman based approach for rapid reconstruction of quantitative susceptibility maps1Radiology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States, 2Bioengineering, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
This abstract presents a novel Split Bregman (SB) based approach to enable rapid minimization of the quantitative susceptibility reconstruction formulation that includes a weighted least squares fidelity constraint and a total variation (TV) penalty. The purpose of this approach is to develop a rapid minimization technique that does not need complex matrix factorization or computation of matrix preconditioners to accelerate convergence. Rapid minimization is achieved by the application of two variable substitutions, one to the weighted fidelity constraint and the other to the total variation term. Minimization of the cost functional is achieved by the novel combination of FISTA based iterative re-weighting and soft thresholding.
Introduction
Magnetic susceptibility has the potential to provide detailed quantitative information about hemorrhagic stroke [1,2], impaired tissue oxygen consumption [2] and neuronal demyelination [2] in clinical MRI examinations. However, reconstruction of tissue magnetic susceptibility maps from the local magnetic field is a challenging ill-posed inverse problem. A combination of weighted least squares fidelity constraint and regularization constraints such as total variation (TV) [3] or total generalized variation (TGV) [4] are used to reduce the inverse problem ill-posedness. A QSM competition [5] comparing several techniques found the most accurate techniques, as compared to COSMOS [6], used compressed sensing strategies to estimate spatial frequency content in the ill-conditioned domain. These techniques preserved sharp features and reduced artifacts, although incurring convergence penalty. Our objective was to develop an efficient QSM algorithm using two variable substitutions [7], called the Quantitative susceptibility mapping Accelerated Reconstruction Technique (QUART). We hypothesized that the new algorithm would produce high quality susceptibility maps while substantially reducing the reconstruction time.Methods
The cost functional to be minimized is given by: $$ C =\frac{1}{2} \parallel M(DF\chi-F\phi)\parallel _2^2 +\lambda \mid W \triangledown\chi \mid _{1} (1) $$
where M is a weighting factor, D is the dipole kernel in Fourier domain, is the tissue field and is the magnetic susceptibility. The cost functional consist of a weighted least squares fidelity term and a total variation based constraint to remove the streaking artifacts. The following variable substitutions are made to eq (1),$$$ A=DF \chi $$$ and $$$ S=W\triangledown \chi $$$. Enforcing the variable substitutions using SB, eq (1) can be rewritten as Here α and β are weights that enforce the SB variable substitution and B and T come from optimizing the Bregman distance [7]. The variables A and $$$ \chi $$$ can be quickly minimized using the FISTA iterative re-weighting scheme [8]. The variable S is minimized using soft-thresholding [7] while the variables B and T are minimized using a linear update step [7]. We compared the results from QUART to thresholded k-space division (TKD) [9], closed form L2-regularized inversion [3] and FANSI [4], a variable substitution implementation of MEDI [10]. The techniques were tested on a COSMOS phantom [4] and cardiac QSM data in a large animal model of hemorrhagic myocardial infarction. These techniques were compared using visual inspection and image quality metrics such as RMSE [5], SSIM [5], HFEN [5] and blur [11]. The reconstruction time of the different implementations was also computed.
Results
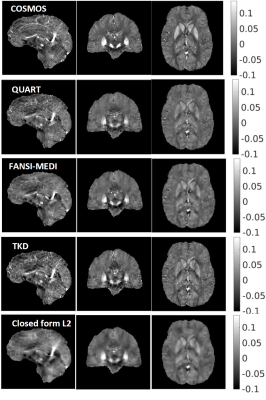
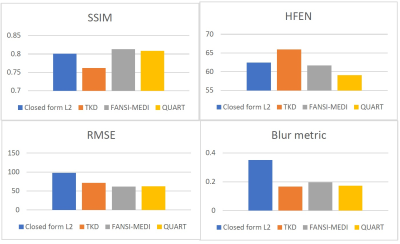
Fig (1) shows the results from the COSMOS phantom. The TKD and closed form L2 technique had the fastest reconstruction time (~.2 sec). The reconstructions from the closed form L2 had image blurring and large RMSE. The TKD technique performed better at reducing image blur and preserving anatomical boundaries, although it had increased HFEN and enhanced streaking artifacts. FANSI-MEDI and QUART produced better quality reconstructions compared to TKD and closed form L2. These techniques produced susceptibility maps with lower RMSE, HFEN and blur metric and while achieving higher SSIM. The reconstruction time of the proposed QUART technique was 43 sec while that of the FANSI-MEDI was 98 sec. This corresponds to a two-fold reduction in reconstruction time. Fig 3 shows the results from a large animal model of hemorrhagic myocardial infarction. The hemorrhagic region seen in Fig (3) A is well visualized in the QUART reconstructions and the increase in susceptibility is seen.Discussion
The major advantage of QUART is its simple, yet efficient, formulation. QUART does not employ matrix factorization techniques and does not need to compute preconditioners like those used in [12,13]. It rapidly minimized Eq. (1) in less than 50 sec. There are differences in the visual quality between FANSI-MEDI and QUART reconstructions, likely attributed to the differences in QSM model and sparsifying constraint. Merely optimizing for lower error metrics often produced smoothed images [5]. Hence, instead of optimizing the techniques for least error metrics, the weights were tuned to ensure that the reconstructed susceptibility maps had a balance of preservation of sharp features and reduced streaking artifacts. The long reconstruction times associated with traditional minimization techniques have prevented the use of sparsity based QSM formulations in a routine clinical setting. The short reconstruction time of QUART (~50 sec) could facilitate clinical application of regularized QSM formulation.Conclusion
In summary, we developed a method for rapid acceleration of QSM reconstruction. QUART had similar image quality to FANSI-MEDI,but had ~50% decrease in the reconstruction time. A short reconstruction time and a simple formulation are the two important features of the proposed QUART technique.Acknowledgements
This work is supported by R00-HL108157, McCabe Foundation, and W.W. Smith Foundation.References
1.Chang S, Zhang J, Liu T, Tsiouris A J, Shou J, Nguyen T and Kovanlikaya I. (2016). Quantitative Susceptibility Mapping of Intracerebral Hemorrhages at Various Stages. JMRI, 44(2), 420–425.
2. Wang Y and Liu T. (2015), Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn. Reson. Med., 73: 82–101. doi:10.1002/mrm.25358
3. Bilgic B, Chatnuntawech I, Fan A P, Setsompop K, Cauley S F, Wald L L and Adalsteinsson E. (2014), Fast image reconstruction with L2-regularization. J. Magn. Reson. Imaging, 40: 181–191. doi:10.1002/jmri.24365.
4. Milovic C, Bilgic B, Zhao B, Acosta-Cabronero J and Cristian Tejos , A Fast Algorithm for Nonlinear QSM Reconstruction, ISMRM 2017.
5. Langkammer C, Schweser F, Shmueli K, Kames C, Li X, Guo L, Milovic C, Kim J., Wei H, Bredies K, Buch S, Guo Y, Liu Z, Meineke J, Rauscher, A., Marques, J. P. and Bilgic, B. (2017), Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn. Reson. Med. doi:10.1002/mrm.26830.
6.Liu T, Spincemaille P, de Rochefort, Kressler B and Wang Y. (2009), Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn. Reson. Med., 61: 196–204. doi:10.1002/mrm.21828
7. Goldstein T and Osher S, The Split Bregman Method for L1-Regularized Problems, SIAM Journal on Imaging Sciences 2009 2:2, 323-343
8. Beck A, and Teboulle M, A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems, SIAM Journal on Imaging Sciences 2009 2:1, 183-202
9. Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magnetic Resonance in Medicine. 2011; 66(3):777–783.
10. Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P and Wang Y. (2013), Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn Reson Med, 69: 467–476. doi:10.1002/mrm.24272.
11. Crete-Roffet F, Dolmiere T, Ladret P, Nicolas M, The Blur Effect: Perception and Estimation with a New No-Reference Perceptual Blur Metric, SPIE Electronic Imaging Symposium Conf Human Vision and Electronic Imaging (January 2007).
12. Liu Z, Kee Y, Zhou D, Wang Y and Spincemaille P. (2017), Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping. Magn. Reson. Med., 78: 303–315. doi:10.1002/mrm.26331.
13. Bilgic B, Fan A P, Polimeni J R, Cauley S F, Bianciardi M, Adalsteinsson E, Wald L L and Setsompop K. (2014), Fast quantitative susceptibility mapping with L1-regularization and automatic parameter selection. Magn. Reson. Med., 72: 1444–1459. doi:10.1002/mrm.25029
Figures