4990
Whole Brain Background Field Removal using Spherical Mean Value Filtering and Local Polynomial Approximation for Quantitative Susceptibility Mapping1Research and Development Group, Hitachi, Ltd., Tokyo, Japan, 2Healthcare Business Unit, Hitachi, Ltd., Tokyo, Japan
Synopsis
We propose a novel background-field removal method to recover a local field of a brain edge. The proposed method consists of two steps. First, the background field of the brain edge is calculated from the total field by using local polynomial approximation. Second, the local field of the whole brain is calculated by regularization that enables sophisticated harmonic artifacts reduction for phase data (RESHARP) processing with the constraint term of the background field of the brain edge. The results from a human brain experiment showed that the method is useful for calculating the local field and susceptibility maps of the whole brain.
Introduction
Quantitative susceptibility mapping (QSM) is very useful for obtaining biological information such as iron content. To calculate susceptibility distribution of biological tissue, it is necessary to calculate a local field of biological tissue. The local field can be obtained by removing a harmonic background field from the total field acquired by MR scan. Typical methods for background-field removal are sophisticated harmonic artifacts reduction for phase data (SHARP)1 and projection onto dipole fields (PDF)2. The former uses the spherical mean value (SMV) theorem to extract the background field. The latter uses the Hilbert projection theorem to extract the background field inside the brain. Both methods have their own advantages and disadvantages. The SHARP or regularization enabled SHARP (RESHARP)3 methods both have a problem in that they cannot calculate the local field of the brain edge corresponding to the radius of the SMV convolution kernel. In this study, to recover the local field of the brain edge, we developed and here propose the background-field removal method that combines a local polynomial approximation and RESHARP. We also demonstrate the results obtained in a healthy volunteer experiment utilizing the proposed method.Methods
Algorithm
The proposed method consists of two steps. First, the background field of the brain edge is calculated from the total field using local polynomial approximation. Second, the local field of the whole brain is calculated by the RESHARP processing method with a constraint term of the background field of the brain edge. The formulation of the proposed method is
$$argmin_{B_{local}}\left[\parallel W_{in}F^{-1}CF\left(B_{total}-B_{local}\right)\parallel_2^2 + \lambda\parallel W_{in}B_{local} \parallel_2^2 + \parallel W_{edge}\left(B_{total}-B_{local}-B_{edge}\right)\parallel_2^2\right] ...... (1),$$
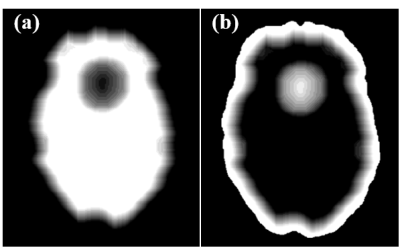
where Btotal and Blocal are respectively the total field and the background field of the whole brain. Bedge is the background field of the brain edge, F and F-1 respectively denote Fourier and inverse Fourier transform matrices, C is the SMV convolution kernel after Fourier transform3, λ is a regularization parameter, and Win and Wedge are weight matrices. As shown in Fig. 1(a) and (b), Win and Wedge change the spatial weights inside the brain and at its edge. By solving equation (1), the local field map of the whole brain can be calculated.
Human brain experiment
A healthy volunteer experiment was performed on a 3T MRI scanner (Hitachi Ltd., Japan) using a 3D RSSG (RF-spoiled-Steady-state Acquisition with Rewound-Gradient-Echo) sequence. The main parameters were: TR = 35 ms, TE = 7.0/11.2/16.2/20.8/25.4/30 ms, FA = 15°, FOV: 192 × 240 × 200 mm, matrix: 204 × 256 × 100 (zero filled to 408 × 512 × 200), and scan time: 4:30. The human brain images were obtained in accordance with the standards of the internal review board on the Research & Development group, Hitachi, Ltd., following receipt of written informed consent. The 3D phase images were calculated from the complex multi-echo images by using the magnitude weighted nonlinear least-squares method. The total field was calculated by using Laplace-based unwrapping from the phase images. In the local polynomial approximation of the proposed method, the fitting range was 5 × 5 × 5 mm and the fitting order was on the second order. The radius of the SMV kernel size was 5 mm and the regularization parameter λ was 10-4. The local field map calculated by using the method was compared with those obtained with RESHARP and PDF methods. Susceptibility maps were reconstructed from the local field maps calculated by the three methods. The QSM reconstruction method was the least-square estimation method with adaptive edge-preserving filtering (LSE-AEPF)4. We visually compared the local-field and the susceptibility maps calculated by the three methods.
Results and Discussion
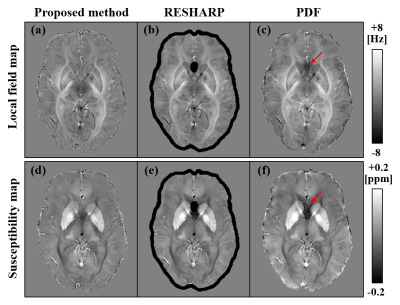
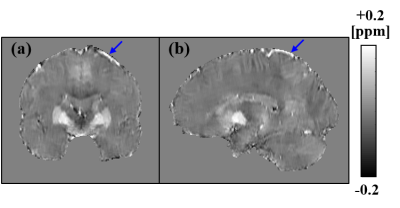
Figure 2 shows the local-field maps (upper row) and susceptibility maps (bottom row) obtained using different background-field removal methods. The black regions shown in (b) and (e) represent the brain edges that cannot be calculated by using the conventional RESHARP method. The regions were recovered by using the proposed method. The red arrows shown in (c) and (f) show the artifacts caused by the residual background field in the PDF method. The artifacts were removed by using the proposed method. Figure 3 shows the susceptibility maps respectively calculated by using the proposed method with coronal (a) and sagittal slices (b). The blue arrows shown (a) and (b) are the veins recovered by the proposed method. The proposed method made it possible to recover the brain edge of the susceptibility and reduce the artifacts caused by the background field.Conclusion
We developed and propose a novel background-field removal method that combines polynomial fitting and RESHARP. The results obtained in a human brain experiment showed that the method is useful for calculating local-field and susceptibility maps of the whole brain.Acknowledgements
This research is partially supported by the project for development of medical devices and systems for advanced medical services (17he1402002h0002) from Japan Agency for Medical Research and development, (AMED).
We wish to thank Dr. Kohsuke Kudo for the useful advice he provided during the course of this study.
References
1. Ferdinand Schweser, et al. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism? Neuroimage. 2011;54:2789-2807.
2. Tian Liu, et al. A novel background field removal method for MRI using projection onto dipole fields (PDF). NMR Biomed. 2011; 24:1129-1136.
3. Hongfu Sun and Alan H. Wilman. Background field removal using spherical mean value filtering and Tikhonov regularization. Magn. Reson. Med. 2014; 71:1151-1157.
4. Toru Shirai, et al. Quantitative Susceptibility Mapping Using Adaptive Edge-Preserving Filtering. Proc. Int. Soc. Magn. Reson. Med. 2015; 23:3319.
Figures