4914
k-t2 ESPIRiT – Image reconstruction of respiratory motion resolved undersampled 4D Flow MRI data in a higher-dimensional subspace1ETH Zurich, Zurich, Switzerland
Synopsis
An image reconstruction algorithm termed k-t2 ESPIRiT is proposed, which constrains respiratory motion-resolved MRI to a high-dimensional subspace spanned by receiver-coil channels, cardiac phases, and respiratory motion states. Respiratory motion resolved 4D flow MRI data is reconstructed and compared to k-t ESPIRiT reconstruction of end-expiration and a standard parallel imaging protocol. Increased reconstruction accuracy compared to k-t ESPIRiT reveals that k-t2 ESPIRiT can effectively exploit redundancies between respiratory motion states to improve scan efficiency.
Synopsis
Respiratory motion is a major source of artifacts in MR imaging and often leads to low scan efficiencies in combination with respiratory gating approaches. Scans which are too long for breathholds are acquired in a respiratory-gated acquisition and only data measured during end-expiration are used for the image reconstruction.
Respiratory motion resolved magnetic resonance imaging (MRI)1,2,3 promises increased scan efficiency by making use of data from all respiratory motion states. In this work, we propose an efficient framework for motion resolved image reconstruction, based on the extension of k-t ESPIRiT4 to include the respiratory motion dimension and apply it for the reconstruction of 4D flow MRI data.
Theory
In self-consistency based parallel imaging (PI) methods, data correlations are derived from a fully sampled training region to enforce consistency in an iterative image reconstruction procedure5,6. For dynamic MRI, the methods were extended by incorporating a spatiotemporal consistency kernel in a higher-dimensional k-t space4,7,8.
When data are recorded with a respiratory motion dimension, extending the k-t space to a higher dimensional k-t2 space was shown to improve reconstruction accuracy2. We therefore propose to extend k-t ESPIRiT to a higher dimensional k-t2 ESPIRiT reconstruction according to:
$$ \underset{x}{\operatorname{argmin}} ||\Omega\mathcal{F} {E}_{c,t^2}(x)-y||_2^2 +\lambda||\Psi x||_1\> .$$ where the k-t2 correlations are incorporated in the encoding operator . $$$\Omega$$$ represents the sampling pattern and $$$\mathcal{F}$$$ is the spatial Fourier transform. $$$\lambda$$$ is the regularization weight and $$$\Psi$$$ is the sparsifying transform. Here, $$$\Psi$$$ was set to the Fourier transform along cardiac phases and respiratory motion states.
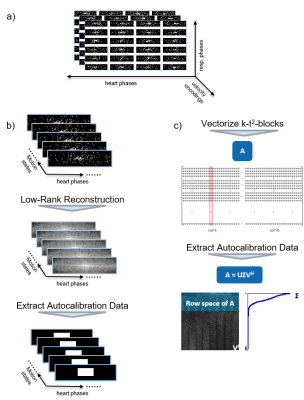
Following9, the encoding operator $$$E_{c,t^2}$$$ is calculated via the null space of an autocalibration matrix built from a fully sampled center region in k-t2 space. However, measuring a fully sampled k-space region for all motion states and heart phases would severely limit the acceleration factor. Instead, a low-rank reconstruction with a relatively small regularization weight is performed on the undersampled data to remove aliasing noise before computing from a k-space center region:
$$ \underset{x}{\operatorname{argmin}} ||\Omega\mathcal{F} \mathcal{S}(x)-y||_2^2 +\lambda||x||_*\> , \ X \in \mathcal{C}^{N_x \times N_{hp} N_{kv}} .$$ The procedure is illustrated in Figure 1.
Methods
Acquisition
4D Flow data in the aortic arch of a healthy volunteer was acquired on a 3T Philips Ingenia system (Philips Healthcare, Best, the Netherlands) using a Cartesian four-point phase-contrast gradient-echo sequence with uniform venc of 220 cm/s and a spatial resolution of 2.5x2.5x2.5 mm3. Data were recorded with a 28 channel receiver coil and compressed to 5 virtual channels with geometric coil compression10. A pseudo-radial Cartesian sampling pattern with Golden angle increments11 was used to ensure sampling incoherency in all respiratory states and cardiac phases. The respiratory motion signal was extracted with self-gating and coil clustering12. The measured data were binned into 6 different motion states with equal acceleration factors of approximately 10 for each respiratory state. As a reference, a navigator-gated scan was acquired with SENSE13 with an acceleration factor of 2 and using a 5 mm navigator window.
Reconstruction and Postprocessing
Eq. 1 was solved with a projection onto convex sets algorithm14 in MATLAB and the low-rank reconstruction was performed with fast iterative shrinkage thresholding15. For comparison, data in end expiration were reconstructed with k-t ESPIRiT4.
Coil sensitivity maps for SENSE and the low-rank reconstruction were calculated from a separate calibration scan using ESPIRiT9.
Concomitant field correction was applied to the signal phase according to16 and eddy currents were corrected for with a linear model fitted to stationary tissue17.
Results
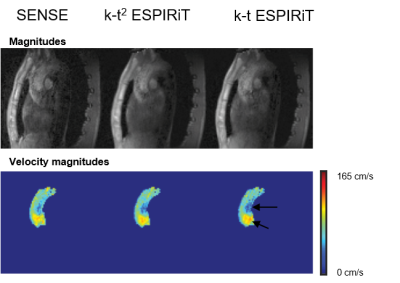
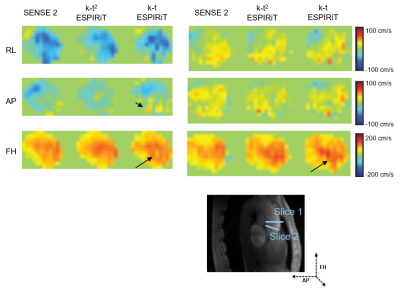
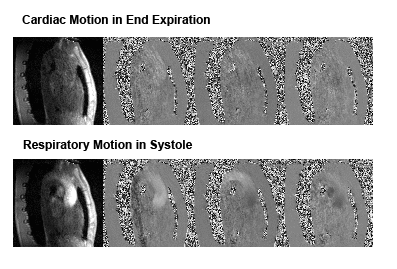
Example reconstruction results are shown in Figure 2. Lower noise levels can be observed for k-t2 ESPIRiT relative to k-t ESPIRiT. An analysis of velocity components in selected slices during systole in Figure 3 also shows higher reconstruction accuracy for k-t2-ESPIRiT relative to k-t ESPIRiT. In Figure 4, an animation of respiratory motion resolved 4D flow reconstructed with k-t2 ESPIRiT is provided.Discussion
This work has provided advances towards improved reconstruction accuracy from undersampled 4D flow MRI data by exploiting redundancies between different motion states and thus making the modality less dependent on respiratory motion. Respiratory motion resolved data can be reconstructed in a higher-dimensional subspace based on an eigendecomposition of data extracted from the k-space center. Moreover, a low-rank reconstruction approach was successfully employed to interpolate missing samples in the k-space center, thus making the method independent of the k-space trajectory. In future investigations, more advanced methods will be considered for this purpose, e.g. structured low-rank completion18.
In summary, k-t2 ESPIRiT holds promise for accelerated 4D Flow MRI with high independence of respiratory motion. In future investigations, the robustness of the method will be investigated with respect to different respiratory motion patterns in order to evaluate benefits for clinical practice.
Acknowledgements
No acknowledgement found.References
[1] J. Y. Cheng, T. Zhang, M. T. Alley, M. Uecker, M. Lustig, J. M. Pauly, and S. S. Vasanawala, “Comprehensive multi-dimensional MRI for the simultaneous assessment of cardiopulmonary anatomy and physiology,” Sci. Rep., vol. 7, no. 1, p. 5330, 2017.
[2] A. Sigfridsson, L. Wigström, J. P. E. Kvitting, and H. Knutsson, “k-t2 BLAST: Exploiting spatiotemporal structure in simultaneously cardiac and respiratory time-resolved volumetric imaging,” Magn. Reson. Med., vol. 58, no. 5, pp. 922–930, 2007.
[3] L. Feng, L. Axel, H. Chandarana, K. T. Block, D. K. Sodickson, and R. Otazo, “XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing,” Magn. Reson. Med., vol. 75, no. 2, pp. 775–788, 2016.
[4] C. Santelli and S. Kozerke, “L1 k-t ESPIRiT: Accelerating Dynamic MRI Using Efficient Auto-Calibrated Parallel Imaging and Compressed Sensing Reconstruction,” J. Cardiovasc. Magn. Reson., vol. 18, no. 1, p. P302, Jan. 2016.
[5] M. A. Griswold, P. M. Jakob, R. M. Heidemann, M. Nittka, V. Jellus, J. Wang, B. Kiefer, and A. Haase, “Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA),” Magn. Reson. Med., vol. 47, no. 6, pp. 1202–1210, 2002.
[6] M. Lustig and J. M. Pauly, “SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space,” Magn. Reson. Med., vol. 64, no. 2, pp. 457–471, 2010.
[7] F. Huang, J. Akao, S. Vijayakumar, G. R. Duensing, and M. Limkeman, “K-t GRAPPA: A k-space implementation for dynamic MRI with high reduction factor,” Magn. Reson. Med., vol. 54, no. 5, pp. 1172–1184, 2005.
[8] C. Santelli, T. Schaeffter, and S. Kozerke, “Radial k-t SPIRiT: Autocalibrated parallel imaging for generalized phase-contrast MRI,” Magn. Reson. Med., vol. 72, no. 5, pp. 1233–1245, 2014.
[9] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA,” Magn. Reson. Med., vol. 71, no. 3, pp. 990–1001, 2014.
[10] T. Zhang, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “Coil compression for accelerated imaging with Cartesian sampling,” Magn. Reson. Med., vol. 69, no. 2, pp. 571–582, 2013.
[11] J. Y. Cheng, T. Zhang, M. T. Alley, M. Lustig, S. S. Vasanawala, and J. M. Pauly, “Variable-density radial view-ordering and sampling for time-optimized 3D Cartesian imaging,” in Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, 2013.
[12] T. Zhang, J. Y. Cheng, Y. Chen, D. G. Nishimura, J. M. Pauly, and S. S. Vasanawala, “Robust self-navigated body MRI using dense coil arrays,” Magn. Reson. Med., vol. 76, no. 1, pp. 197–205, 2016.
[13] K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med., vol. 42, no. 5, pp. 952–962, 1999. [14] L. G. Gubin, B. T. Polyak, and E. V Raik, “The method of projections for finding the common point of convex sets,” USSR Comput. Math. Math. Phys., vol. 7, no. 6, pp. 1–24, 1967.
[15] A. Beck and M. Teboulle, “A Fast Iterative Shrinkage-Thresholding Algorithm,” Soc. Ind. Appl. Math. J. Imaging Sci., vol. 2, no. 1, pp. 183–202, 2009.
[16] M. A. Bernstein, X. J. Zhou, J. A. Polzin, K. F. King, A. Ganin, N. J. Pelc, and G. H. Glover, “Concomitant gradient terms in phase contrast MR: Analysis and correction,” Magn. Reson. Med., vol. 39, no. 2, pp. 300–308, 1998.
[17] P. G. Walker, G. B. Cranney, M. B. Scheidegger, G. Waseleski, G. M. Pohost, and A. P. Yoganathan, “Semiautomated method for noise reduction and background phase error correction in MR phase velocity data,” J. Magn. Reson. Imaging, vol. 3, no. 3, pp. 521–530, 1993.
[18] P. J. Shin, P. E. Z. Larson, M. A. Ohliger, M. Elad, J. M. Pauly, D. B. Vigneron, and M. Lustig, “Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion,” Magn. Reson. Med., vol. 72, no. 4, pp. 959–970, 2014.
Figures