Synopsis

Cardiac MRI acquisitions require accurate triggering, usually derived from ECG. The contactless, electromagnetic Pilot Tone navigator enables direct measurement of cardiac and respiratory motion, independently of the acquisition. Here we present an almost lag free pipeline to process the cardiac Pilot Tone signal and derive triggers from it.

Introduction

Methods

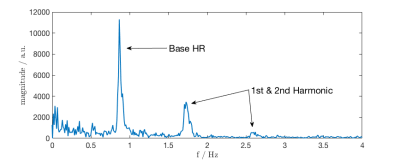
Measurements were performed at 1.5T (MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany) on four volunteers (3 male, 1 female, 1.58-1.76m, 52-106kg, BMI: 20.8-40.8). The PT signal was generated by a small battery-powered device positioned anterior of the volunteer's heart and extracted from raw-data in the scanner's reconstruction environment using prototype software. Prior to real-time processing, a calibration step is performed in which 20-40s of PT raw-data are processed using Independent Component Analysis (FastICA⁴, algorithm: deflationary, contrast-function: gauss, # of ICs:12) in order to separate the cardiac signal $$$s_{card}(t)$$$ from the mixture of sources received in each channel². We use Principal Component Analysis (PCA) prior to ICA for dimensionality reduction (34 $$$\rightarrow$$$ 16 dimensions) by retaining the 16 largest singular values. The cardiac signal component is identified by visual inspection. Following this calibration step, incoming data (see Fig. 2) are processed in real-time to separate $$$s_{card}(t)$$$ by multiplication with the unmixing matrix computed by ICA. The noisy cardiac data stream is then fed into an Extended Kalman Filter (EKF) using a phenomenological state-space model $$$\widetilde{s}_{card}(t)$$$ of $$$s_{card}(t)$$$ motivated by Fourier-analysis. Figure 2 shows the frequency-domain representation of $$$s_{card}(t)$$$: Peaks corresponding to base heart-rate and one or two harmonics can be identified, thus $$$s_{card}(t)$$$ can be modeled with high quality in the time-domain by Fourier-synthesis yielding

$$\widetilde{s}_{card}(t) = c(t) + a_0(t) \sin \left(2 \pi f(t) + \varphi_0(t) \right) + a_1(t) \sin \left( 4 \pi f(t) + \varphi_1(t) \right) \quad \quad \quad \textrm{Eq. 1}$$

where $$$c(t)$$$ is an offset term, $$$f(t)$$$ base heart-rate and $$$a_{0,1}(t)$$$ and $$$\varphi_{0,1}(t)$$$ amplitude and phase of the base- and harmonic frequency. $$$\widetilde{s}_{card}(t)$$$ was then computed for each incoming sample and subsequently used as input to a triggering algorithm which detects maxima of $$$\widetilde{s}_{card}(t)$$$.

To test the quality of the EKF output signal and triggers generated from it, we simulated the real-time acquisition process by implementing the EKF in Matlab and using raw $$$s_{card}(t)$$$ data as input. Goodness of fit was assessed by comparing $$$\widetilde{s}_{card}(t)$$$ against retrospectively filtered (FIR, N=2000, $$$f_c=4\textrm{Hz}$$$) $$$s_{card,ref}(t)$$$ using normalized mean squared error (NMSE)

$$ NMSE = 1 - \frac{ ||s_{card,ref}(t)-\widetilde{s}_{card}(t)||_2^2}{||s_{card,ref}(t)- \textrm{mean}(s_{card,ref}(t))||_2^2} \quad \quad \quad \textrm{Eq. 2}$$

as a criterion. Additionally, residuals should be gaussian in the absence of systematic fitting errors.

Trigger quality was tested by comparing trigger-times obtained from $$$\widetilde{s}_{card}(t)$$$ to those from ECG ground-truth as $$$t_{ECG}-t_{PT}$$$.

Results

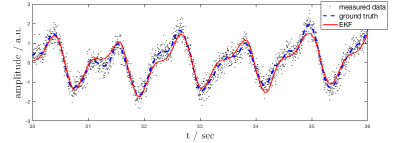
The EKF was able to accurately follow the noisy input data in all volunteers. Figure 3 shows EKF output vs. retrospectively filtered PT raw data. At the beginning of each measurement, the EKF took between 5-10s to stabilize, depending on the accuracy of the parameters default initial guess. NMSE was close to 1 in all volunteers, indicating excellent fit of $$$\widetilde{s}_{card}(t)$$$ to ground-truth. Residuals were gaussian in all cases (Kolmogorov-Smirnov test).

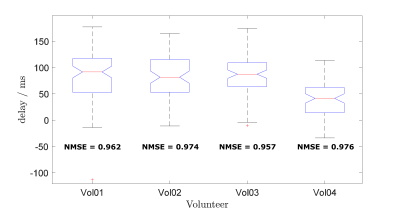
Comparing trigger-points to ECG, we found PT triggers to be some 40-80ms earlier than those from ECG. Figure 4 shows boxplots of time-differences. Whiskers represent the 1.5 Inter-Quartile-range of time-differences, i.e. a measure of trigger-jitter. Note that the electromechanical delay, i.e. the time from ECG R-wave to onset of cardiac motion is known to be subject to variance⁵, explaining at least part of the observed jitter as PT measures cardiac motion directly.

Discussion & Conclusion

The phenomenological model used in the EKF appears to be suitable to describe the complexities of the cardiac PT signal. While some higher-frequency detail is lost, important features like maxima and minima are accurately represented and appear suitable for triggering. A disadvantage of this model is that, except frequency, the used parameters do not model physiologically relevant parameters.

While some of the observed time-delay can certainly be attributed to processing-delay in the ECG, PT triggers appearing 40-80ms earlier than ECG R-wave could indicate that PT is sensitive to atrial contraction.

Our results show that virtually lag free real-time processing of the cardiac PT signal is feasible using the presented model based de-noising approach by Extended Kalman Filtering. To evaluate the method further we plan to apply the method to prospectively triggered Cine acquisitions for gold standard comparison.

Acknowledgements

References

[1] P. Speier et al. "PT-Nav: A Novel Respiratory Navigation Method for Continuous Acquisition Based on Modulation of a Pilot Tone in the MR-Receiver", Proc. ESMRMB 129:97-98, 2015

[2] M. Bacher et al. "Retrospective Evaluation of Pilot Tone Based CardiacTrigger Quality In A Volunteer Cohort", Book of Abstracts ESMRMB 2017 30:360-361, 2017

[3] L. Schroeder et al. "Two-Dimensional Respiratory-Motion Characterization for Continuous MRMeasurements Using Pilot Tone Navigation". In Proc. Intl. Soc. Mag. Reson.Med. 24:3103, 2016

[4] [4] A. Hyvärinen, ‘‘Fast and robust fixed-point algorithms for independentcomponent analysis’’, IEEE Transactions on Neural Networks, vol. 10, no. 3, pp. 626–634

[5] C. I. O. Brookes et al. "Myocardial contractility is not constant during spontaneous atrial fibrillation in patients", Circulation", 98:1762–1768,1998