Synopsis

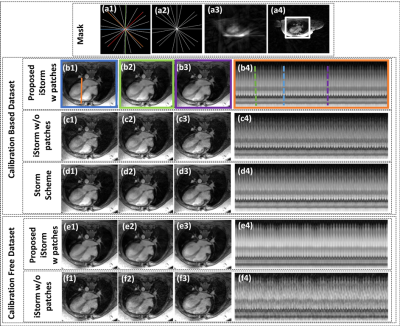
Self-gated acquisitions, which rely on navigator acquisitions, can offer shortened scan time and can enable cardiac imaging of patients who cannot hold their breath; they are emerging as promising alternatives to breath-held protocols. A challenge with such schemes is the inefficiencies associated with the navigator acquisition, as well as the need for complex and heuristic processing of the navigator signals to accurately determine the cardiac and respiratory phases. The focus of this work is to introduce a navigator-less acquisition and reconstruction strategy, built upon our recent work termed as SToRM, which exploits the manifold structure of images. The proposed framework eliminates the need for navigators in SToRM, in addition to enabling spatially localized manifold modeling, where the manifold structure can vary depending on the spatial structure.

Introduction

Methods

We formulate the proposed framework to recover the dynamic dataset F as the following optimization problem:

\begin{equation}\mathbf F^{*} = \arg \min_{\mathbf F} \|\mathcal A (\mathbf F)-\mathbf B\|^{2}_{2}+ \lambda_{1} \sum_{\mathbf r_k} ~\underbrace{ \sum_{i=1}^{N_{f}} \sum_{j=1}^{N_{f}} \varphi\left(\|\mathbf P_{\mathbf r_k}(\mathbf f_i) - \mathbf P_{\mathbf r_k}(\mathbf f_j)\|\right)}_{\mathcal C(\mathbf r_k)},\end{equation}

The second term is the proposed manifold smoothness penalty where both image patches or image frames can be used to estimate the manifold structure. Here, $$$\mathcal P_{\mathbf r}(\mathbf f_i)$$$ is a patch extraction operator, which extracts a square shaped 2-D image patch of dimension $$$(N+1)\times (N+1)$$$, centered at the spatial location $$$\mathbf r$$$ from $$$\mathbf f_i$$$, which is the $$$i^{\rm th}$$$ frame in the dataset. The main differences between this formulation and (3) is the use of unweighted robust distances between patches in the dataset, rather than the weighted quadratic distances between images used in (3). We choose the distance metric as $$$\varphi(t)= 1-\exp(-t^2/2\sigma^2)$$$.We use an alternating algorithm, which alternates between estimating the weights as \begin{equation}w_{i,j}(\mathbf r) = \exp\left(-\frac{\|\mathcal P_{\mathbf r_k}(\mathbf f_i) - \mathcal P_{\mathbf r_k}(\mathbf f_j)\|^2}{2\sigma^2}\right)\end{equation}and updating the images as \begin{equation}\mathbf F^{*} = \arg \min_{\mathbf F} \|\mathcal A (\mathbf F)-\mathbf B\|^{2}_{2}+ \lambda_{1} \sum_{\mathbf r_k} ~\sum_{i=1}^{N_{f}} \sum_{j=1}^{N_{f}} w_{i,j}(\mathbf r)~\|\mathcal P_{\mathbf r_k}(\mathbf f_i) - \mathcal P_{\mathbf r_k}(\mathbf f_j)\|^2\end{equation} Note that the above equation is equivalent to SToRM, when a single patch is considered; the main difference is that the weights are derived from the images themselves rather than navigators, which facilitates the use of local manifold structure. The above alternating strategy is inspired by PRICE (4), where we used similar approaches to exploit the similarity of patches in adjacent images. We typically use 3-4 iterations.

Results

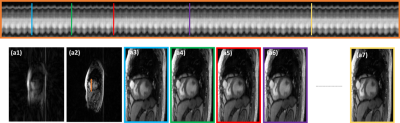
The proposed scheme is validated on two free-breathing ungated datasets acquired using FLASH sequence on Siemens 3T Skyra scanner at the University of Iowa Hospital. The datasets were acquired with 10 radial lines per frame, with and without using navigators. The sequence parameters were: TR/TE 4.3/1.92 ms, FOV 300mm, Base resolution 256, Bandwidth 574 Hz/pix. 10000 spokes of k-space were collected in 43 s. Figure 1 shows the recovery of the proposed scheme iSToRM, with and without using patches, vs the state-of-the-art navigator-based SToRM. The calibrated based dataset has 4 navigator signals as shown in a(1) while the calibration-free dataset is acquired without navigators a(2). Figure 2 shows the recovery of another dataset acquired from a different patient using the patch-based scheme. The proposed patch-based framework provides comparable image quality to SToRM with fewer motion artifacts and without relying on any navigator signals.

Conclusion

Acknowledgements

References

1: Feng L, et al. XD-GRASP: Golden-angle radial MRI with the reconstruction of extra motion-state dimensions using compressed sensing. MRM. 2016.

2: HJ Huang et al. Super-resolution hyperspectral imaging with unknown blurring by low-rank and group-sparse modeling, IEEE ICIP, 2015.

3: Poddar S et al. Dynamic mri using smoothness regularization on manifolds (storm). IEEE TMI, 2016.

4: Mohsin YQ, et al. Accelerated dynamic mri using patch regularization for implicit motion compensation. MRM, 2016.

5: Yang Z et al. Nonlocal regularization of inverse problems: a unified variational framework. IEEE TIP 2013.