4898
Dynamic Auto-calibrated Multiband CAIPIRINHA: proof of principle and application to cardiac tissue phase mapping1Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany, 2Centre for the Developing Brain, Department of Perinatal Imaging & Health, Division of Imaging Sciences & Biomedical Engineering, King´s College London, London, United Kingdom, 3Department of Radiology, Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 4Department of Radiology, Feinberg School of Medicine, Northwestern University, Chicago, IL, United States, 5Department of Biomedical Engineering, McCormick School of Engineering, Northwestern University, Chicago, IL, United States
Synopsis
In conventional multiband CAIPIRINHA, an additional reference scan is acquired to allow the separation of the simultaneously excited slices. In this study, an acquisition-reconstruction method that makes use of the multiband data itself to calculate this reference scan is presented. The immediate implication is that the full multiband acceleration can be exploited. In addition, since the reference data has the same resolution and phase structure to multiband (i.e. it is the same data), improved slice separation is achieved. The method was implemented starting from a 2D CINE phase-contrast MR sequence, and it was used to assess velocities in the myocardium in two subjects scanned at 3T.
Introduction
Multiband imaging using controlled-aliasing-in-parallel-imaging-results-in-higher-acceleration (CAIPIRINHA)1 allows the simultaneous acquisition of multiple slices (SMS)2 with low g-factor penalties at reconstruction. Initially, multiband has been applied to the brain3, but has also been extended to time-resolved cardiac imaging4,5,6,7.
In this study, we extend the CAIPIRINHA framework to allow the calculation of built-in reference data in dynamic applications, thus without requiring additional reference scans. The framework was first tested using time-resolved (CINE) 7T data taken from Ref.5 that has been retrospectively modified. It was then implemented into a prospectively-triggered 2D CINE phase-contrast MR sequence and applied to tissue phase mapping8 with/without respiratory navigation at 3T.
Methods
Sequence and Principle
Fig.1a illustrates the k-space line dependent CAIPIRINHA RF phase shifts for the second slice in Multiband2 (MB2) CINE gradient-echo-imaging (GRE). The alternating $$$\pi$$$ shift is constant for all cardiac phases and results in a FOV/2 shift of slice2. Similarly, MB3 can be achieved as shown in Fig.1b-c. We propose modified patterns in time as shown in Fig.1d-f. By linear combinations of groups of two (three) neighboring cardiac phases, this pattern allows reconstructing un-aliased, (effective) low-temporal-resolution images from aliased MB2 (MB3) data. This low-temporal-resolution data is then used for kernel calibration to reconstruct9 the MB data at high temporal resolution.
Reference calculation
If we label with $$$m_{s,p}^{l}$$$ the generative complex k-space signal of line $$$l$$$ from slice $$$s$$$ ($$$1≤s≤MB$$$) at cardiac phase $$$p$$$, then the measured multiband k-space signal $$$m_p^{l}$$$ is a summation over the bands weighted by the line/slice/cardiac-phase-dependent CAIPIRINHA phases $$$\theta_{s,p}^{l}$$$:
$$m_p^{l}=\sum_{s = 1}^{MB}m_{s,p}^{l}e^{i\theta_{s,p}^{l}}$$
By considering only the group of adjacent cardiac phases $$$p,p+1,...,p+MB-1$$$, the following set of linear equation can be written:
$$\left(\begin{array}{c}m_p^{l}\\m_{p+1}^{l}\\\vdots\\m_{p+MB-1}^{l}\end{array}\right)=\begin{bmatrix} e^{i\theta_{1,p}^{l}}&e^{i\theta_{2,p}^{l}}&\cdots&e^{i\theta_{MB,p}^{l}}\\e^{i\theta_{1,p+1}^{l}}&e^{i\theta_{2,p+1}^{l}}&\cdots&e^{i\theta_{MB,p+1}^{l}}\\\vdots&\ddots&\ddots&\vdots\\e^{i\theta_{1,p+MB-1}^{l}}&e^{i\theta_{2,p+MB-1}^{l}}&\cdots&e^{i\theta_{MB,p+MB-1}^{l}}\end{bmatrix}\left(\begin{array}{c}m_{1,p}^{l}\\m_{2,p}^{l}\\\vdots\\m_{MB,p}^{l}\end{array}\right)$$
and, after matrix inversion, a low-temporal resolution single band signal $$$m_{s,p}^{l}$$$ can be retrieved under the assumption that $$$m_{s,p}^{l}=m_{s,p+1}^{l}=\cdots=m_{s,p+MB-1}^{l}$$$ - thus the generative lines do not change within the time required to acquire MB cardiac phases.
If we consider, for example, the case of $$$MB=2$$$ and $$$p=1$$$, the pattern in Fig.1d in combination with the presented framework translates into solving two distinct sets of linear equations for odd and even lines:
$$\left(\begin{array}{c}m_{1,1}^{odd}\\m_{2,1}^{odd}\end{array}\right)={\begin{bmatrix}e^{i0}&e^{i0}\\e^{i0}&e^{i\pi}\end{bmatrix}}^{-1}\left(\begin{array}{c}m_1^{odd}\\m_{2}^{odd}\end{array}\right)={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}^{-1}\left(\begin{array}{c}m_1^{odd}\\m_{2}^{odd}\end{array}\right)={\begin{bmatrix}0.5&0.5\\0.5&-0.5\end{bmatrix}}\left(\begin{array}{c}m_1^{odd}\\m_{2}^{odd}\end{array}\right)$$
$$\left(\begin{array}{c}m_{1,1}^{even}\\m_{2,1}^{even}\end{array}\right)={\begin{bmatrix}e^{i0}&e^{i\pi}\\e^{i0}&e^{i0}\end{bmatrix}}^{-1}\left(\begin{array}{c}m_1^{even}\\m_{2}^{even}\end{array}\right)={\begin{bmatrix}1&-1\\1&1\end{bmatrix}}^{-1}\left(\begin{array}{c}m_1^{even}\\m_{2}^{even}\end{array}\right)={\begin{bmatrix}0.5&0.5\\-0.5&0.5\end{bmatrix}}\left(\begin{array}{c}m_1^{even}\\m_{2}^{even}\end{array}\right)$$
Finally, note that the framework is easily extendable for $$$MB>3$$$.
Reconstruction
The reference data is averaged in time to reduce motion artifacts such that two averaged datasets exists for MB2 (one for even, one for odd cardiac phases). Three averaged datasets are generated for MB3. MB slices are then separated using a slice-GRAPPA algorithm9 using 9x9 kernels derived from averaged reference data. Note that for flow encoded scans each encoding value/direction is treated independently.
Simulations and Experiments
The framework was first tested on a previously acquired breath hold 7T-GRE cine single-band (SB) dataset (see Ref.5,Tab.1,Subject3). Here, k-space data of the three SB slices were added after modulating each slice/line/cardiac phase according to Fig1e-f and data was reconstructed using the aforementioned formalism. Leakage was obtained as in Ref.5 (see Figure caption).
Then, time-resolved velocity-encoded phase-contrast images were obtained with MB2 in short axis cardiac view in two subjects with/without breath-hold at 3T (Magnetom Verio, Siemens, Germany) during three separate scanning sessions (Tab.1) to map the myocardial motion. Additional low-resolution non-time-resolved data was acquired to enable standard reconstructions with external references.
Finally, reconstruction signal leakage5 and velocities over the myocardium as treated in8 are presented and compared to multiband.
Results
Fig.2 demonstrates successful slice separation for the retrospectively
reconstructed MB3 dataset5 showing no apparent signal of other slices.
In vivo, residual mean leakage in the non-breath-hold scan
(Fig.3,left;red arrows) of the fatty tissue (evaluated within the selected
masks shown in the figure) was found to decrease from 24.5±7.2% to 13.4±3.4% for slice1,
and from 20.6±6.5% to 12±3.2% for slice2 when comparing standard versus our method. Fig.3 (right) shows the separated
slices in the breath-hold acquisition using: an external reference (left), our method (center) and single-band matched slices (right). Residual artifacts are visible occasionally in the MB data, leakage maps (Fig.3h) and in the SB data, likely resulting from blood flow. Generally, leakage values of the background tissue are reduced using our method.
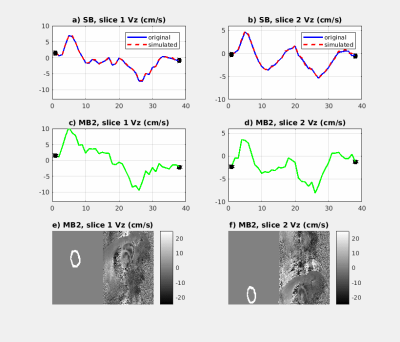
Finally, Fig.4 demonstrates that i) the same flow values in SB and artificial MB2 datasets can be obtained and ii) that the actual MB2 dataset shows similar flow values to SB.
Discussion and Conclusion
We propose a new technique to reconstruct prospective cardiac cine-MB data using a built-in reference that omits the necessity to acquire additional time-consuming reference scans. When applying the method to breath holds images, residual “leakage-like” signal was observed in both the reconstructed MB data and the SB data. We attribute these artifacts to fast motion of the blood, however, further investigations are needed, e.g. by saturating the blood. Despite this, plausible flow measurements were obtained.
Acknowledgements
References
1. Breuer FA, Blaimer M, Heidemann RM, et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 2005;53(3):684–691.
2. Larkman DJ, Hajnal JV, Herlihy AH et al. Use of multicoil arrays for separation of signal from multiple slice s simultaneously excited. J. Magn. Reson. Imaging. 2001;13:313–317.
3. Feinberg AD and Setsompop K. Ultra-Fast MRI of the Human Brain with Simultaneous Multi-Slice Imaging. J Magn Reson. Imaging. 2013;229:90–100.
4. Lau AZ, Tunnicliffe EM, Frost R et al. Accelerated human cardiac diffusion tensor imaging using simultaneous multislice imaging. Magn. Reson. Med. 2015;73(3):995-1004.
5. Schmitter S, Moeller S, Wu X et al. Simultaneous multislice imaging in dynamic cardiac MRI at 7T using parallel transmission. Magn. Reson. Med. 2016;77(3)1010–1020.
6. Stäb D, Ritter CO, Breuer FA, et al. CAIPIRINHA accelerated SSFP imaging. Magn. Reson. Med. 2011;65(1):157–164.
7. Price AN, Grande LC, Malik SJ, et al. Accelerated Cine Imaging of the Heart using Blipped Multiband SSFP. In Proceedings ISMRM 2017 Honolulu USA.
8. Jung B, Markl M, Foll D, et al. Investigating myocardial motion by MRI using tissue phase mapping. European Journal of Cardio-thoracic Surgery 2006;S150–S157.
9. Setsompop K, Gagoski BA, Polimeni JR, et al. Blipped‐controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g‐factor penalty. Magn. Reson. Med. 2012;67:1210–1224.
Figures
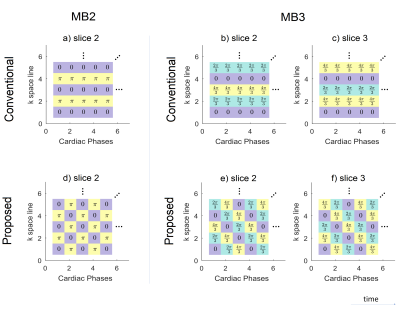

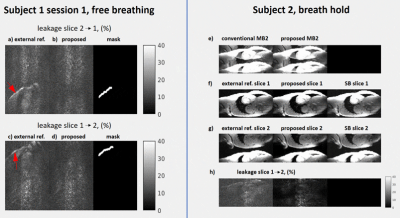
Fig.3: Left; In vivo leakage maps (subject 1 session number 1) using: a) and c) the low resolution reference data, b) and d) our built-in reference approach. Maps were normalized by the average signal value found in the myocardium5, and the masks used for leakage quantification are reported to the right. Right; MB breath-hold acquisitions (e, subject 2), separated slices 1 (f) and 2 (g) using conventional MB2 (left), the proposed approach (center). SB data is reported to the right for reference. (h) Leakage maps in % of slice 1 into 2.

Tab.1: Data acquisition details in all sessions. In all acquisitions, an anterior cardiac coil with 16 elements in conjunction to a posterior spine coil with 12 elements were used.