4889
Expanding SMS cardiac imaging with deep slice interpolation1Radiology and Imaging Sciences, University of Utah, Salt Lake City, UT, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
Cardiac SMS imaging acquires multiple slices at the same time as a single slice. SMS provides increased slice coverage without a loss in temporal resolution, which is important in myocardial perfusion imaging. However, a single SMS acquisition is able to acquire three slices at a time, which is insufficient for whole heart coverage. This work expands SMS coverage by using new deep learning interpolation techniques to generate missing slices in the "gaps" between acquired slices in SMS imaging.
Introduction
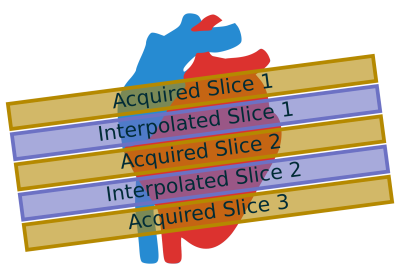
Simultaneous multi-slice (SMS) imaging acquires multiple slices at the same time as a single slice[1]. This technique has been expanded to radial imaging[2] in cardiac MRI. SMS increases slice coverage without a loss of temporal resolution, which is particularly important in myocardial perfusion imaging. Slice interpolation can achieve additional heart coverage without increasing acquisition times. Adjacent SMS slices could be used to generate missing slices, thereby reducing the number of SMS acquisitions, increasing temporal resolution, and maintaining spatial resolution. Figure 1 shows an illustration of this approach.
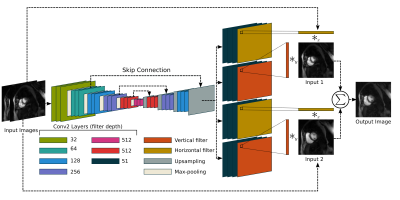
Interpolation is an active area of research in both medical imaging[3] as well as traditional image processing fields[4]. In medical imaging, increasing the slice-direction resolution is similar to video frame rate interpolation. Adaptive separable convolution[5] is an appropriate interpolation method. This work uses a deep network to determine convolution kernels for each pixel of two adjacent time frames (two adjacent slices in the MRI context). A traditional 2-dimensional convolution is simplified by using a separable convolution with a vertical and horizontal kernel. This eases memory and computational load as the size of the kernel is reduced from $$$n^2$$$ to $$$2n$$$ elements. Figure 2 shows an illustration of this network. This network is well-suited for SMS application as it requires adjacent slices only instead of a large volume, which is not feasible with SMS, for its interpolation. We propose using adaptive separation convolution interpolation with cardiac SMS imaging as a deep slice generation technique (DeepSlice) in order to increase scan coverage without increasing the number of acquisitions.
Methods
DeepSlice used an adaptive separable convolution neural network [5] trained with MRI-specific training. Figure 2 shows this network and process flow. Our loss function was
$$$\left\lVert \phi(I_\text{learned}) - \phi(I_\text{target}) \right\rVert^2_2,$$$
where $$$\phi(\cdot)$$$ is a feature extraction function based on the relu4_4 layer of the VGG-19 network, similar to the original [5] approach. Optimization was done through the Adamax algorithm, with a learning rate of 0.001, β1 of 0.9, and β2 of 0.999. The batch size was 16. All implementations were done using the PyTorch framework. We also used a naive linear interpolation where two slices are averaged to produce the gap slices for comparison.
The DeepSlice network was initially trained on video data and fine-tuned using studies where five slices were acquired without cardiac gating, with 50 ms readouts. In each study, the five slices were acquired approximately four times per second, for 60 seconds[6]. The training data included both at rest and regadenoson stress acquisitions. Because the cardiac phases were similar in adjacent slices in these rapid ungated acquisitions, this is reasonable training data for SMS applications. All images were reconstructed as magnitude images using the Spatio-Temporal Constrained Reconstruction (STCR)[7]. Slice gaps were created by taking three adjacent slices, using the center slice as target image and the two outside slices as the inputs to the network, giving an interpolation pair. For each set of five slices covering the heart, three interpolation pairs can be generated. The training dataset had a total of 30,000 interpolation input image pairs. We used an 80/20 training/validation split. Each slice had a matrix size of 144x144. The DeepSlice approach was compared against this reference standard as well as the linear interpolation using structural similarity (SSIM), peak signal-to-noise ratio (PNSR), mean squared error (MSE) metrics. This method was ultimately applied to SMS datasets with a multi-band factor of 3 and gaps equal to the slice thickness between the slices. Ground “truth” in the SMS case comes from a second block acquisition with interleaved slices. Consequently, these second set of slices were acquired at a different time in the cardiac cycle.
Results
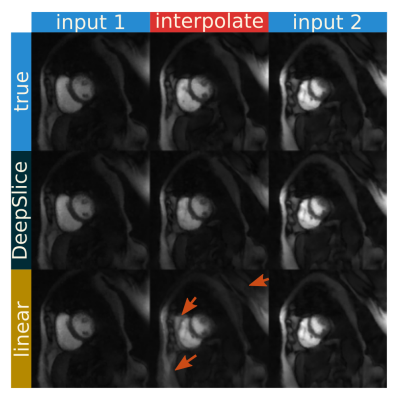
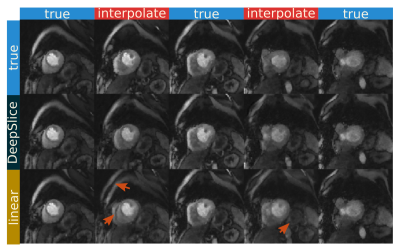
Figure 3 shows the deep slice approach provides images similar to ground truth. The linear interpolation method does show more deviations from the ground truth image. From a quantitative standpoint, the deep slice approach similarly outperforms linear interpolation, giving an SSIM score of 0.840±.08, a PSNR value of 30.4±3.5, and an MSE value of 0.0051±0.0044. The linear interpolation method gives an SSIM score of 0.78±0.06, a PSNR value of 23.5±3.1, and an MSE value of 0.0057±0.0039. With SMS data, DeepSlice interpolation also appears to avoid many of the artifacts seen in the linear interpolation and provides a reasonable interpolation compared to the ground truth. This is despite the ground truth being acquired in a different time in the cardiac cycle than the input data.Discussion and Conclusion
DeepSlice is a state-of-the-art method to generate missing slices that is well-suited for expanding cardiac SMS coverage thereby reducing the number of acquisitions. The results demonstrate the promise of this technique, showing quantitative superiority over naive methods and presenting visually appealing examples in this initial work.Acknowledgements
The authors thank Simon Niklaus for his insight into his work on the adaptive separable convolution network. We also want to gratefully acknowledge funding from NIH T32HL007576-31 and NIH HL135328.References
[1] Breuer, Felix A., et al. "Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi‐slice imaging." Magnetic resonance in medicine 53.3 (2005): 684-691.
[2] Wang, Haonan, et al. "Radial simultaneous multi-slice CAIPI for ungated myocardial perfusion." Magnetic resonance imaging 34.9 (2016): 1329-1336.
[3] Neubert, Aleš, et al. "Constrained reverse diffusion for thick slice interpolation of 3D volumetric MRI images." Computerized Medical Imaging and Graphics 36.2 (2012): 130-138.
[4] Baker, Simon, et al. "A database and evaluation methodology for optical flow." International Journal of Computer Vision 92.1 (2011): 1-31.
[5] Niklaus, Simon, Long Mai, and Feng Liu. "Video Frame Interpolation via Adaptive Separable Convolution." arXiv preprint arXiv:1708.01692 (2017).
[6] Bieging, Erik T., et al. "Rapid rest/stress regadenoson ungated perfusion CMR for detection of coronary artery disease in patients with atrial fibrillation." The International Journal of Cardiovascular Imaging (2017): 1-8.
[7] Adluru, Ganesh, et al. "Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging." Journal of Magnetic Resonance Imaging 29.2 (2009): 466-473.
Figures