4873

Free-breathing and ungated 3D-T1rho mapping of the heart using golden angle radial sampling and compressed sensing with low-rank constrained sparse reconstruction
Rajiv G Menon1, Marcelo V.W. Zibetti1, Azadeh Sharafi1, Li Feng1, Leon Axel1, and Ravinder R Regatte1

1New York University School of Medicine, New York, NY, United States

Synopsis

In this study, we present a technique for T1rho mapping of myocardium using a combination of T1rho preparation, radial sampling, and low rank-based compressed sensing (CS) reconstruction. We acquire free-breathing, ungated data using a 3D T1rho prepared radial acquisition scheme with different spin lock times (TSL). After retrospectively synchronizing the data to a window in diastole, a sparse 3D k-dataset is given as input to compressed sensing reconstruction that uses a low rank constraint. Mono-exponential modeling of the reconstructed data yields the T1rho maps. The CS reconstruction results in improved images and the mean T1rho values estimated in the myocardium are consistent with literature.

Introduction

Ischemic heart disease is one of the leading causes of mortality in humans1. Late gadolinium enhancement (LGE) is the top choice for characterizing myocardial tissue. but its use of contrast agent precludes many patients with renal clearance dysfunctions. Hence, development of non-invasive techniques to detect myocardial infarcts, edema and myocardial fibrosis is highly desirable. T1rho cardiovascular magnetic resonance (CMR) is emerging as an endogenous contrast method to characterize the heart non-invasively2-3. In this study, we present a technique that uses a combination of T1rho preparation, golden-angle radial sampling, and a low-rank based compressed sensing reconstruction scheme to perform T1rho mapping for characterizing the myocardium non-invasively.

Methods

Imaging Sequence and Data Acquisition

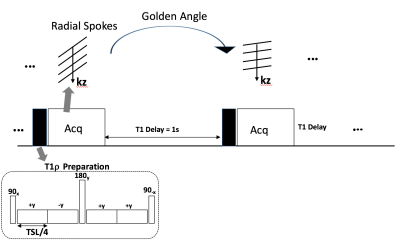
The imaging sequence consisted of a RAVE (RAdial Volumetric Encoding) sequence4 with a customized T1rho preparation module5. A 3D golden-angle, stack-of-stars radial sampling trajectory was used to acquire all spokes along the kz-dimension in each TR. One second delay was inserted between consecutive TRs to allow for T1 decay. Five healthy volunteers (3 male, 2 female, age=28 ± 6 years) were recruited following informed consent. The imaging study consisted of a 3D free-breathing acquisition with the in-plane direction aligned along the short axis orientation of the heart. The resolution was 1.6x1.6x2.0 mm3. FOV=300mm2, TR=5ms, TE=2ms, in-plane radial spokes = 200, acquisition matrix=384x200x44, T1rho spin lock frequency=350 Hz, 10 spin lock duration (TSL) datasets were obtained with TSL= [2,4,6,8,10,15,25,35,45,55]. Acquisition time for each TSL was 4 minutes, resulting in a total acquisition time of 40 minutes. Each radial stack was acquired in 200ms. Electrocardiogram (ECG) leads were connected, and the ECG logs were saved for the duration of the acquisition.

ECG Synchronization

Using the start-times of the data acquisition from raw data and ECG logs, the ECG triggers were synchronized with the start times of each radial spoke stack. A window of 200 ms prior to each trigger was used in order to choose the spokes in mid to late diastole. For each accepted spoke, all the spokes along the kz dimension were included too. This resulting sparse 3D k-data was used as input to compressed sensing reconstruction. In addition to compressed sensing the sparse k-data was reconstructed using a gridding algorithm.

Compressed Sensing using Low Rank Prior

The compressed sensing reconstruction problem is formulated as: $$x=\arg\min_x ||m-FCx||_2^2+λ||X||_*.$$ where $$$x$$$ represents the image series to be reconstructed (different TSLs), $$$C$$$ is the coil sensitivities, $$$F$$$ represents the NUFFT operator, and $$$λ$$$ is the regularization parameter. The low rank (LR) regularizer utilize the nuclear-norm6 $$$||X||_*$$$, where $$$X$$$ is $$$x$$$ reshaped as space-time matrix, and each row contains the complex magnetization signal of a voxel over TSLs.

T1rho Mapping

After reconstruction, curve fitting is performed to generate the T1rho map using a mono-exponential model: $$|x(t,n)|=a(n)exp\left(\frac{-t}{τ(n)} \right)+b,$$ where $$$a(n)$$$ is magnitude, while $$$τ(n)$$$ is the T1rho relaxation time. Non-linear least squares is utilized as cost function, where the minimization is done utilizing conjugate gradient Steihaug’s trust-region7. A 3x3 voxel averaging is utilized prior to the fitting process.

Results

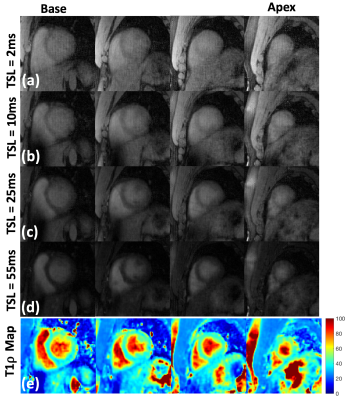
Figure 2(a-d) shows gridding reconstruction of the ECG synchronized sparse k-data for different TSL durations. The resulting T1rho map is shown in figure 2(e). Figure 2(f-i) shows the results from the compressed sensing reconstruction. The resulting T1rho map is shown in figure 2(k). Compressed sensing results in significant reduction of streaking artifacts, and improved resulting T1rho maps. Figure 3 rows (a) through (d) show the reconstructed images from base to apex at different TSL durations. The last row, figure 3 (e) shows the T1rho maps calculated from the CS reconstruction. The mean T1rho in myocardium was 50.48 ± 5.58 ms.

Discussion and Conclusion

In this study, we demonstrated the use of golden-angle radial sampling and compressed sensing reconstruction for 3D T1rho mapping of the heart. Retrospective sorting of radial spokes in synchronization with ECG logs and compressed sensing significantly reduce the streaking artifacts and image blurring compared to gridding reconstruction,and the computed T1rho maps are consistent with literature.

Acknowledgements

This study was supported by NIH grants R01-AR060238, R01 AR067156, and R01 AR068966, and was performed under the rubric of the Center of Advanced Imaging Innovation and Research (CAI2R), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

  1. Yancy, CW, et al. 2013 ACCF/AHA guideline for the management of heart failure: a report of the american college of cardiology foundation/american heart association task force on practice guidelines. Circulation. 2013;128:e240–327. doi: 10.1161/CIR.0b013e31829e8776.
  2. Muthupillai R, Flamm SD, Wilson JM, Pettigrew RI, Dixon WT. Acute myocardial infarction: tissue characterization with T1rho-weighted MR imaging—initial experience. Radiology. 2004;232:606–610. doi: 10.1148/radiol.2322030334.
  3. Witschey WR, Pilla JJ, Ferrari G, Koomalsingh K, Haris M, Hinmon R, Zsido G, Gorman JH, 3rd, Gorman RC, Reddy R. Rotating frame spin lattice relaxation in a swine model of chronic, left ventricular myocardial infarction. Magn Reson Med. 2010;64:1453–60. doi: 10.1002/mrm.22543
  4. Benkert T, Feng L, Sodickson DK, Chandarana H, Block KT. Free-breathing volumetric fat/water separation by combining radial sampling, compressed sensing, and parallel imaging, Magn Reson Med, 10.1002/mrm.26392 (2016)
  5. Sharafi A, Xia D, Chang G, Regatte RR. Biexponential T1rho relaxation mapping of human knee cartilage in vivo at 3 T. NMR Biomed. 2017 (In Press)
  6. K. C. Toh and S. Yun, “An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems,” Pacific J. Optim., vol. 6, no. 3, pp. 615–640, 2010.
  7. T. Steihaug, “The conjugate gradient method and trust regions in large scale optimization,” SIAM J. Numer. Anal., vol. 20, no. 3, pp. 626–637, Jun. 1983.

Figures

Figure 1: Acquisition scheme. The T1rho preparation module consists of four segments with alternative phase to compensate for B1 inhomogeneities. A 180° refocusing pulse was applied between two pairs for B0 inhomogeneity compensation. One radial phase line from all slices is acquired after applying the preparation module. This is followed by a T1 restoration delay of 1 second. During the next preparation, the radial spokes are rotated using a golden angle scheme.

Figure 2: The top row shows gridding reconstruction of ECG synchronized data at different TSL durations (a-d), and the resulting T1rho map obtained from 10 TSL values. The second row show compressed sensing reconstruction with low rank prior to the same data. Figures (f-i) are the results from the compressed sensing reconstruction, and figure (k) is computed T1rho map.

Figure 3: Rows (a) through (d) show from the base to apex short axis views at different TSL durations after compressed sensing reconstruction. The T1rho map in row (e) is computed by mono-exponential fitting to the data from 10 TSLs.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4873