4618
Comparison of Referenceless Methods for EPI Ghost Correction in Breast Diffusion Weighted Imaging1Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, 2Department of Radiology, University of Minnesota, Minneapolis, MN, United States, 3Clinical and Translational Science Institute, University of Minnesota, Minneapolis, MN, United States
Synopsis
Three-line navigator correction of Nyquist ghosts in spin-echo echo-planar imaging (SE-EPI) diffusion weighted imaging (DWI) often fails in body imaging. Several alternative strategies have been proposed including referenceless methods, which do not require any type of reference information but instead minimize a cost function based on the data itself. The purpose of this work is to assess ghost correction of undersampled (R=3) breast DWI using several referenceless methods, including minimization of SVD in k-space, image entropy, a ghost/object ratio of the image, and a combination. All four referenceless strategies outperform the standard navigator correction, providing higher quality images and unbiased ADC maps.
Introduction
Diffusion weighted imaging (DWI) with spin-echo echo-planar imaging (SE-EPI) suffers from artifacts called Nyquist (or N/2) ghosts. These ghosts are commonly corrected using a 3-line navigator1, which is generally robust in brain imaging but often fails in breast imaging due to increased lipid signal, B0 inhomogeneity, and respiration. Alternative ghost correction methods have been proposed, including referenceless methods, which includes the entropy2,3 and SVD4 techniques. These methods do not require any navigator, reference data, or sensitivity profile, and can thus be used with many acquisition schemes. The purpose of this work is to compare the performance of several referenceless methods with the standard 3-line navigator for dynamic ghost correction of breast DWI.Methods
Acquisition
Single-shot 2D SE-EPI DWI was acquired under IRB-approved protocols from 41 female subjects, including healthy volunteers and patients undergoing MRI for screening or treatment monitoring (Table 1). DWI was performed on a Siemens Prismafit 3T system with a Sentinelle 16-channel breast coil, using a protocol derived from the ACRIN 6698 clinical trial5: TR=8 s, TE=51/74 ms (monopolar/bipolar diffusion, N=12/29), GRAPPA acceleration R=3, acquisition time ≤ 5 min. Three-scan traces were acquired (2-3 averages) with b-values between b=0-800 s/mm2. Three-line navigators were acquired with each acquisition.
Reconstruction and ghost correction
First-order ghost correction requires estimation of a linear shift and phase correction to alternating lines of k-space of the form $$$S_{corrected}(k_x,k_{y,odd}) = S_{ghost}(k_x-\kappa,k_{y,odd}) * e^{-i \phi}$$$. Method A represents the standard correction, in which the phase difference between alternating echoes of the 3-line navigator is filtered, weighted, and fit to estimate κ and ϕ.
The referenceless methods minimize a cost function $$$f_{cost}(\kappa, \phi)$$$ using a simplex minimization in Matlab (fminsearch). In method B (“Entropy”) the cost function is the image entropy2,3; in method C (“SVD”) fcost is the summation over the tail of singular values after rearranging k-space into GRAPPA-like kernels4; in method D (“Ghost/Object”) fcost is the summation of the ratio between the image and its FOV/2-shifted replica6. The final method (E, “Median”) combines the referenceless methods as $$$\kappa_{median} = \text{median}(\kappa_B, \kappa_C, \kappa_D)$$$ and $$$\phi_{median} = \text{median}(\phi_B, \phi_C, \phi_D)$$$. For all referenceless methods, the GRAPPA autocalibration (ACS) data were used to estimate initial correction parameters for the undersampled data. The solutions were dynamically refined by minimizing fcost on single-channel data after unaliasing with ghost-corrected ACS lines. ADC maps were generated using a pixel-by-pixel log-linear fit over the b-values.
Analysis
The severity of ghost artifacts was assessed by measuring the signal intensity in the background of the images determined by semi-automatic thresholding and dilation of T1-weighted anatomical images (3D GRE). The background to noise ratio (BNR) was defined as the mean background signal compared to a case-specific noise measurement in the corner of the image. To compare method performance, the per-volume BNR measurements were fit to a linear mixed model including the effects of method, b-value, and subject BMI. All five methods were compared in a pairwise manner, adjusting for multiple comparisons using Tukey-Kramer’s method.
Results
All referenceless methods yielded reduced ghosts compared to the standard approach. Whole volume BNRs are plotted in Figure 1a on a per-slice and b-value basis. Similarly, individual BNR values were compared between the referenceless methods and standard navigator in Figure 1b. The distributions of per-volume BNRs are shown for each b-value in Figure 2.
According to the linear mixed model, the method (p<0.0001), b-value (p<0.0001), and BMI (p=0.0256) significantly affect the BNR; however, the interaction between b-value and method is not significant. The pairwise comparisons between each method are reported in Table 2. All four referenceless methods yielded lower BNR values (p<0.0001) than method A. There was no statistically significant difference between the referenceless methods (B,C,D,E), although the median method (E) yielded the lowest ghost level at all b-values.
Figure 3 shows images of a single b=0 s/mm2 average and ADC maps from a single slice of two cases that represent successful and failed corrections by the linear navigator.
Discussion
Referenceless ghost correction methods are advantageous because they do not require a navigator or reference data, potentially allowing for reduced TE and/or scan time, and they can be applied retrospectively to EPI data acquired with various acquisition strategies. Concerns about the failure of these methods on aliased data4 were circumvented by refining the cost function minimization after GRAPPA reconstruction. Referenceless methods can be extended for higher order corrections at the cost of increased computation time. While BNR was used as a surrogate metric to compare performance, the primary concern is ghosts overlaying the foreground, which can bias ADC values.Conclusions
Referenceless ghost correction methods outperformed the standard 3-line navigator in breast DWI, providing higher quality images and reduced bias in ADC maps.Acknowledgements
NIH P41 EB015894
NIH R21 CA201834
References
- Heid, O. (2000). Method for the phase correction of nuclear magnetic resonance signals.
- Clare, S. (2003). Iterative Nyquist ghost correction for single and multi-shot EPI using an entropy measure. In Proceedings of the 16th Annual Meeting of ISMRM, Toronto, Canada, p. 1041.
- Skare, S., Clayton, D.B., Newbould, R., Moseley, M., and Bammer, R. (2006). A fast and robust minimum entropy based non-interactive Nyquist ghost correction algorithm. In Proc. Intl. Soc. Mag. Reson. Med, (Seattle, Washington), p. 2349.
- Peterson, E., Aksoy, M., Maclaren, J., and Bammer, R. (2015). Acquisition-free Nyquist ghost correction for parallel imaging accelerated EPI. In Proc. Intl. Soc. Mag. Reson. Med., (Toronto, Ontario), p. 0075.
- Partridge SC, Zhang Z, Newitt DC, Gibbs JE, Chenvert TL, Rosen MA, Bolan PJ, Marques HS, Esserman LJ, Hylton NM. ACRIN 6698 Trial: Quantitative Diffusion-Weighted MRI to Predict Pathologic Response in Neoadjuvant Chemotherapy of Breast Cancer. In Proceedings of ASCO, Chicago, 2017
- McKay JA, Moeller S, Ramanna S, Auerbach EJ, Metzger GJ, Ryder JR, Ugurbil K, Yacoub E, Bolan, PJ. (2017) Novel Image-based Nyquist Ghost Correction of Diffusion-Weighted Echo Planar Imaging with Ghost/Object Minimization. In Proceedings of the 26th Annual Meeting of ISMRM [Submitted]
Figures


Figure 1. Ghost measurements for every subject and every acquisition over whole volumes. a) BNR b) pair-wise difference in BNR between method A and referenceless methods (B, C, D, E). In (a) lower values indicate more complete ghost suppression; in (b), negative values indicate cases in which the given referenceless method outperformed the linear navigator. Referenceless methods generally produce reduced ghosts compared to the standard approach.
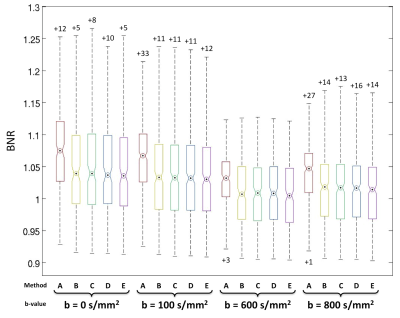
Figure 2. Boxplots of BNR values over full volumes for every method separated by b-value. Circles indicate median, numbers indicate outliers. All four referenceless methods outperform the standard navigator for every b-value. Although not statistically significant, the median combination (E) yields lower median BNR values than the other referenceless methods (B, C, D) for every b-value.
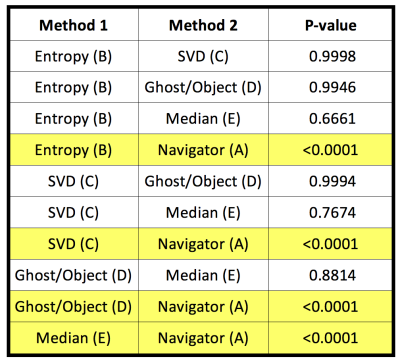
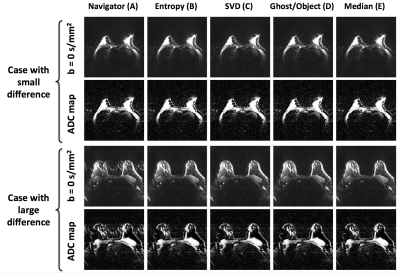
Figure 3. b = 0 s/mm2 images and ADC maps from two example cases that represent navigator success (top) and failure (bottom). Cases were chosen objectively based on the bottom and top 25th percentiles of difference between BNRs from a b = 0 s/mm2 image corrected using linear navigator and referenceless methods. PE is in the right-left direction.