4472
Retrospective removal of gas-phase signal from pulmonary dissolved-phase Hyperpolarized 129Xe images1Department of Medical Physics, University of Wisconsin, Madison, Madison, WI, United States
Synopsis
Dissolved-phase hyperpolarized xenon-129 imaging provides regional information on gas exchange between the lung airspaces, parenchymal tissues, and blood stream. Current spectroscopic techniques require that the dissolved-phase 129Xe signal be acquired with no gas-phase excitation. However, the short T2* of the dissolved-phase requires short RF pulses, limiting the spectral selectivity achievable. This, combined with the high spin density of the gas-phase relative to the dissolved-phase, leads to unwanted gas-phase excitation. In this work, we retrospectively remove contaminant gas-phase signal from both simulated and human subject images using a multi-echo acquisition with iterative estimation of the contaminant gas-phase signal.
Introduction
Spectroscopic imaging of hyperpolarized (HP) xenon-129 dissolved in the lung parenchyma and bloodstream provides regional information on gas exchange [1]. Techniques used to separate HP 129Xe in the barrier tissues and red blood cells (RBC) require signal be acquired without gas-phase excitation [2,3]. However, gas-phase excitation can occur despite careful spectrally selective pulse design due to RF pulse sidelobes that weakly excite the higher density gas signal.
Previously, we presented a technique to retrospectively remove gas-phase signal from dissolved-phase images, estimating the contaminant gas signal using an additional delayed echo acquisition [4]. This method was shown to successfully limit contamination by gas signal to <10% of the dissolved-phase signal, but accuracy was limited by residual dissolved-phase signal in the delayed echo. In the present work, we present an improved multi-echo technique that refines the estimate of gas-phase contaminant signal using a more complete signal model. This technique results in dissolved-phase spectroscopic images with <1% contamination from gaseous HP 129Xe signal, improving performance by an order of magnitude compared to the prior method.
Methods
Theory: We simultaneously acquire multi-echo data at both the gas-phase and dissolved-phase resonant frequencies, as described in [2]. The acquired dissolved-phase data, contaminated with gas-phase signal, can be modeled as follows.
$$s_{d,raw}(\vec{k},t)=s_{d,true}(\vec{k},t)+\alpha s_{gas}(\vec{k},t)e^{2\pi i \Delta ft}$$
$$$s_{d,raw}$$$ and $$$s_{gas}$$$ are the acquired dissolved- and gas-phase data, respectively; $$$\alpha$$$ is a correction factor accounting for the change in excitation of the gas between the dissolved- and gas-phase acquisitions; and $$$\Delta f$$$ is the change in the receive frequency between the dissolved- and gas-phase acquisitions. If $$$\alpha$$$ can be properly estimated, the contaminating gas signal can be subtracted from the dissolved-phase data.
The dissolved-phase signal $$$s_{d,true}$$$ can be expanded in terms of the RBC and barrier components.
$$s_{d,raw}(\vec{k},t)=\rho_{rbc}(\vec{k})e^{(2\pi if_{rbc}-r_{2_{rbc}}^*)t}+\rho_{bar}e^{(2\pi if_{bar}-r_{2_{bar}}^*)t}+\alpha s_{gas}(\vec{k},t)e^{2\pi i\Delta ft}$$
$$$\rho_{rbc}$$$ and $$$\rho_{bar}$$$ are the Fourier transforms of the RBC and barrier spin densities, respectively; and $$$f$$$ and $$$r_2^*$$$ are the frequency shifts and transverse relaxation rates of the components, estimated from global spectroscopy performed prior to imaging.
From this model, we iteratively solve for $$$\rho_{rbc}$$$, $$$\rho_{bar}$$$, and $$$\alpha$$$ until $$$\alpha$$$ converges, as described in Figure 1. Contaminant gas-phase signal may then be subtracted from the dissolved-phase signal based on the equations above.
Simulation: To analyze the performance of this technique, a digital phantom was used to generate gas- and dissolved-phase signals based on a 3D-radial acquisition with 4 gradient echoes (TEs=0.9ms, 2.0ms, 3.1ms, 4.2ms). Early results revealed that accuracy was increased by limiting the estimation to the more fully sampled central region of k-space. As such, we tested the performance against the region of k-space included in the estimation.
Human Subject Imaging: Gas- and dissolved-phase MRI was acquired at 1.5T in a single 15s breathhold using 1L of HP 129Xe and a 3D-radial sequence with 4 echoes. A 1.2ms SLR RF pulse with a 5kHz bandwidth was designed to minimize off-resonance transmit power. Transmit and receive frequencies were alternated between the gas and RBC resonances, acquiring the same projection angles in k-space for both frequencies [2].
Results
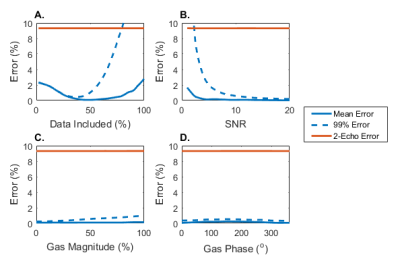
Simulated data indicate the accuracy of this technique is highly dependent on the region of k-space included in the fit, seen in Figure 2, with a minimum error when including the central 40% of the data. Errors increase above 2% in extreme cases of noise (SNR<5), but remain robust for SNR>5. The performance of this technique is unaffected by changes in the contaminant signal. For dissolved-phase images with SNR>7, simulated results indicate reduction of the contaminant gas-phase signal to <1% of the dissolved-phase signal.
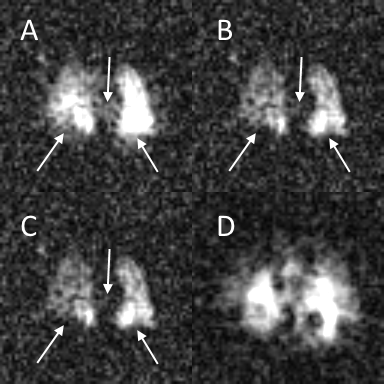
As shown in Figure 3, this technique removes the artifacts caused by the off-resonance gas-phase signal. Qualitatively, the performance appears similar to the previously reported two-echo technique. However, there is a measureable difference between the two techniques in agreement with the difference estimated in the simulated results.
Discussion
The unwanted excitation of the gas-phase signal during dissolved-phase acquisition is difficult to avoid, despite careful RF-pulse design. Current approaches to mitigate gas-phase signal require site-specific calibration of the RF-pulse parameters that can impose tradeoffs on pulse sequence parameters (e.g. flip angle). This presents a barrier to disseminating and replicating methods across sites. Our approach requires no specialized RF-pulse or amplifier calibration, allowing for greater flexibility in pulse sequence design and dissemination.Conclusion
A robust method is presented that reduces signal contamination of dissolved-phase images by unwanted gas-phase excitation to below 1% of dissolved-phase signal. The consequent reduction of spectral contamination will improve the accuracy and repeatability of quantitative ratios used to estimate gas exchange in lung disease.Acknowledgements
The authors would like to acknowledge financial support from NIH/NHLBI R01 Hl126771, NIH/NCRR 1 S10 OD016394 (the Pulmonary Imaging Center), and NIH/NCATS UL1 TR000427 to UW ICTR for funding support.References
- Driehuys B, Cofer GP, Pollaro J, et al (2006) Imaging alveolar-capillary gas transfer using hyperpolarized 129Xe MRI. Proc Natl Acad Sci U S A 103:18278–18283.
- Kaushik SS, Robertson SH, Freeman MS, et al (2016) Single-breath clinical imaging of hyperpolarized (129)Xe in the airspaces, barrier, and red blood cells using an interleaved 3D radial 1-point Dixon acquisition. Magn Reson Med 75:1434–1443.
- Qing K, Ruppert K, Jiang Y, et al. Regional Mapping of Gas Uptake by Blood and Tissue in the Human Lung using Hyperpolarized Xenon-129 MRI. Journal of magnetic resonance imaging : JMRI. 2014;39(2):346-359.
- Kammerman J, Hahn A, Roberson S, Driehuys B, Fain SB (2017) Dissolved phase hyperpolarized Xenon-129 Pulmonary imaging in the presence of gaseous Xenon signal (abstract). In: Proc. Intl. Soc. Mag. Reson. Med. 25. Honolulu, p 2143
Figures