4431
Advancement in Dynamic Sensitivity Averaging for a Rotating RF Coil (RRFC) at 9.4T with Compressed Sensing1School of Information Technology and Electrical Engineering, The University of Queensland, Brisbane, Australia
Synopsis
We have previously developed a practical imaging scheme for the rotating RF coil (RRFC) in Cartesian trajectories. This scheme employs dynamic sensitivity averaging (DSA) of multiple k-spaces during coil rotation, which eliminates the need of time-consuming, position-dependent sensitivity estimation for image reconstruction of the RRFC. As demonstrated in previous work, two extra complementary profiles are required to achieve efficient DSA, thus the scan duration is potentially extended. To further improve the efficiency of DSA, compressed sensing (CS) is implemented to the image reconstruction of the RRFC.
Introduction
A single-element rotating RF coil (RRFC) can collect signal around the imaging subject, producing images comparable to a traditional volume coil 1. To eliminate artefacts caused by coil rotation, multiple algorithms 2-4 based on SENSitivity Encoding (SENSE) 5 have been developed. However, obtaining transmit and receive sensitivity maps at all angular positions can be technically challenging and time-consuming; therefore, we developed practical imaging methods 1,6 to acquire images without estimating sensitivity profiles for both radial and Cartesian trajectories by employing dynamic sensitivity averaging (DSA). Radial sequences have intrinsically oversampled central k-space, which can be used to realise DSA; but for Cartesian trajectories, acquiring a set of three k-spaces are needed for effective DSA, which potentially extends the overall scan time. It is intuitive to exploit fast imaging algorithms to accelerate imaging. In this work, we use Compressed Sensing (CS) 7 to improve Cartesian-trajectory based DSA efficiency.Methods
The rotating loop coil has the same geometry as our previously developed RRFC prototype (Ø: 40 mm, 60° open angle, 26 mm in length) designed for a 9.4 T MRI pre-clinical system 1. The electromagnetic simulation software FEKO (Hyperworks, USA) and Matlab (Massachusetts, USA) was used to generate designated rotation-dependent sensitivity profiles and corresponding k-space samples. As demonstrated in 6, by adjusting rotation speed and imaging parameters, k-space lines are encoded with 120° angular increment and three successive k-spaces are able to generate an artefact-free image with DSA. In order to reduce the total scan duration, randomly undersampled (phase-encoding direction) k-space data will be reconstructed by solving constrained optimisation as:
$$\min\left(\lambda_{1}\parallel\psi m\parallel_{1}+\lambda_{2} TV\left(m\right)\right), s.t. \parallel b-Am\parallel_{2}<\epsilon$$
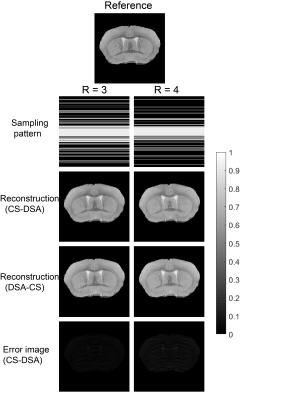
where Ψ is sparsity transform realised by wavelet transform, b is the acquired k-space data, A is the encoding matrix combined with both Fourier and sensitivity encoding, λ1 and λ2 are regularization factor for L1 and total variation (TV), respectively. These two weighting factors were optimally chosen according to the reconstruction quality measured by Peak-SNR (PSNR) and root-mean-square-error (RMSE). In this work, the optimal weighting factors were found as λ1 = λ2 = 0.001. The final images can be reconstructed in two ways from three undersampled k-spaces: 1) use CS to recover individual k-spaces which are encoded with different sensitivity profiles and then apply DSA for the final image recovery; 2) use DSA to combine three undersampled k-spaces into one k-space which are encoded with uniform sensitivity and then apply CS reconstruction. These two reconstruction patterns are referred to as CS - DSA and DSA - CS in Figure 1. The reconstruction is performed by modifying sparse MRI toolbox 7 to incorporate DSA scheme.
Results and Discussion
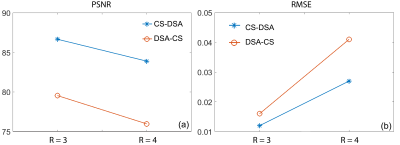
When the reduction factor is equal or higher than three, the total scan time of undersampling three k-spaces is equivalent or less than sampling a full standard k-space using a stationary coil. As shown in Fig. 1, when the reduction factors are three and four, both proposed methods can reconstruct mouse brain images with very small errors when comparing to the reference image, which is reconstructed from three full k-spaces with DSA. However, as shown in Fig. 2, the first method (CS - DSA) is clearly advantageous over the second (DSA - CS), demonstrated with higher PSNR and lower RMSE. The reason is that CS-DSA recovers multiple k-spaces before applying DSA for the final image recovery, which naturally improves SNR and reduce RMSE. In comparison, with DSA - CS, there is only one k-space used for final CS reconstruction, although all k-space lines have uniform sensitivity profiles by applying DSA first.Conclusion
In this proof-of-concept work, we investigated the feasibility of employing CS to improve the efficiency of dynamic sensitivity averaging and retain the overall scan duration to be equivalent to or less than a standard full k-space sampling. The quality of the reconstructed image is comparable to the one reconstructed from DSA without undersampling. This method inherits the advantage of DSA for reconstructing images of RRFC without the need of measuring sensitivity profiles; in addition, the shorter scan time advances the rotating RF technique for practical applications.Acknowledgements
No acknowledgement found.References
1. Li M, Weber E, Jin J, Hugger T, Tesiram Y, Ullmann P, Junge S, Liu F and Crozier S, Radial MRI using a rotating RF coil at 9.4 T, NMR in Biomedicine, 2017, Accepted
2. Trakic A, Wang H, Weber E, Li B, Poole M, Liu F and Crozier S, Image reconstructions with the rotating RF coil, Journal of Magnetic Resonance, 2009, V201, 186-198
3. Li M, Zuo Z, Jin J, Xue R, Trakic A, Weber E, Liu F and Crozier S, Highly Accelerated Acquisition and Homogeneous Image Reconstruction with Rotating RF Coil Array at 7 T — A Phantom Based Study, Journal of Magnetic Resonance, vol. 240, pp.102-112, 2014.
4. Li M, Jin J, Zuo Z, Liu F, Trakic A, Weber E, Zhuo Z, Xue R, Crozier S, In vivo Sensitivity Estimation and Imaging Acceleration with Rotating RF Coil Arrays at 7 Tesla, Journal of Magnetic Resonance, vol. 252c, 29-40, 2015.
5. Pruessmann K, Weiger M, Scheidegger M, Boesiger P, Peter SENSE: Sensitivity Encoding for Fast MRI, Magnetic Resonance in Medcine, 42:952–962, 1999
6. Li M, Jin J, Weber E, Tesiram Y, Hugger T, Stark S, Junge S, Liu F, and Crozier S, A Practical Imaging Scheme for a Rotating RF Coil (RRFC) at 9.4T by Applying Dynamic Sensitivity Averaging, in proceeding International Society for Magnetic Resonance in Medicine, 23th scientific meeting and exhibition, 2015, Honolulu, USA
7. Lustig M, Donoho D, Santos J, Pauly J, Compressed Sensing MRI, IEEE Signal Processing Magazine, V25, 72-82, 2008
Figures