4406
New optimization strategies for RF shimming at UHF MRI1University of Pittsburgh, Pittsburgh, PA, United States
Synopsis
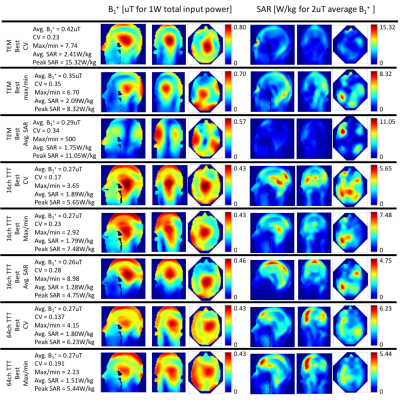
This work proposes four optimization strategies for the RF shimming in UHF MRI. The results show a minimum coefficient of variation of B1+ field distribution over the human head = 23%/17%/14% for the 4chTEM, 16chTTT, and 64chTTT respectively. For the maximum over minimum evaluation criteria of the B1+ field distribution, the best values were 6.70/2.92/2.23 for 4chTEM/16chTTT/64chTTT coils. For a fixed mean B1+ field over the human head, the best average SAR values were 2.09/1.28W/kg for the 4chTEM/16chTTT coils respectively. These strategies can be applied to any RF transmit array system, but are most beneficial for highly parallel systems.
Introduction
RF inhomogeneities still present great challenges in UHF MRI, causing voids/low contrast images and high peak/average SARs, especially when using sequences that require high flip angles. RF shimming potentially improves B1+ field inhomogeneities and reduces peak/average SARs. This work presents different strategies for RF shimming using highly parallel RF transmit arrays.Methods
FDTD simulations were performed using an in-house developed package. The parameters of the simulations are: spatial resolution ~1.6mm isotropic, temporal resolution ~3ps. Three head RF coil designs were simulated and tuned to 297 MHz: a 4-channel 16 elements TEM coil 1, a 16 channel Tic-Tac-Toe (TTT) coil 2, and a 64-channel double row octagon TTT coil 3.
Non-linear constrained optimization was performed using an in-house developed Matlab code (MathWorks; Natick, Massachusetts, United States). The phases and amplitudes of each channel can be manipulated to produce the target RF distribution (amplitudes are limited to the power available in the MRI scanner), what gives up to (N*2-1) degrees of freedom in the optimization, where N is the number of channels of the RF coil.
The optimization algorithm was the interior-point and three objective functions were chosen for the B1+ shimming: coefficient of variation (CV), maximum over minimum of the signal (max/min), and coefficient of variation over minimum (CV/min). Constraints were also included in the optimizations: 1) average B1+ ≥ 0.27189 𝜇𝑇 per 1𝑊 of total input power; 2) in some cases, CV could variate no more than 5% of the initial condition; 3) in some cases, SAR constraints based on virtual observation points (VOPs) were applied. Moreover, the optimizations were performed in 3 different regions of interest: 1) brain only; 2) whole head from cerebellum, excluding the nasal cavities; and 3) whole head from cerebellum. The software was also able to define initial condition from previous optimizations or to define random initial conditions. Figure 1d summarizes the optimization strategies.
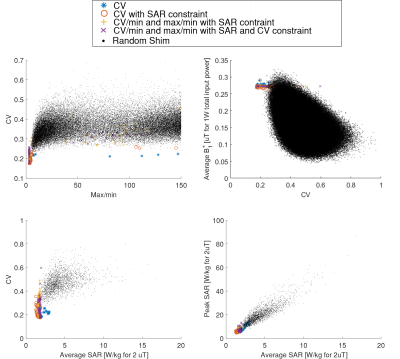
The results were compared with different objective functions and constraints, and, in the case of the 16-channel TTT, to random shimming cases.
Results
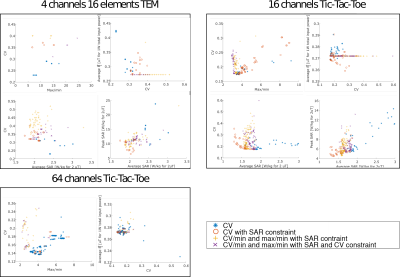
Figure 2 shows the scatter graphs with the results for the three simulated RF coil designs. The graphs present:1) the CV over the max/min of the B1+, where lower values for the two variables are desired; 2) the Average B1+ in 𝜇𝑇 for 1W of total input power over the CV, where the Average B1+ should be enough to guarantee a high flip angle (180 degrees with 1 ms square pulse) and CV should be minimized; 3) the CV over the average SAR in W/kg for 2 𝜇𝑇 of average B1+, where both variables that should be minimized; and 4) the Peak SAR over average SAR, where both variables should be minimized.
Figure 3 shows the comparison between the optimized shimming cases and random shimming cases. Figure 4 shows selected cases with the best CV and max/min for the 3 coils, and the lowest Average SAR for the TEM and 16ch TTT coils. These optimization operational points are on the extremes of the scattering plots, and trade off can the found in between these cases.
Discussions and conclusion
For the TEM coil, the CV strategy showed the best results in terms of B1+ performance, showing lowest values of CV and max/min. In terms of SAR in the TEM, the CV with SAR constraint showed the best results, but the B1+ statistics were not satisfactory. For the 16ch TTT coil, the CV and CV with SAR constraint showed the best results for CV minimization while the max/min with SAR and CV constraint showed the best max/min values. In terms of SAR, the CV with SAR constraint showed the best performance. For the 64-channel TTT coil, CV optimization showed the best results for CV, and max/min with SAR and CV constraint showed the best max/min values.
In conclusion, these optimization strategies are optimal for massively parallel RF systems and the results can be implemented in systems operating in pTx or combined modes.
Acknowledgements
This work was partially funded by the National Institutes of Health R01MH111265 and by the CAPES Foundation, Ministry of Education of Brazil, 13385/13-5.References
1. Vaughan JT, Hetherington HP, Otu JO, Pan JW, Pohost GM. High-Frequency Volume Coils for Clinical Nmr Imaging and Spectroscopy. Magnetic Resonance in Medicine. 1994;32(2):206-18. doi: DOI 10.1002/mrm.1910320209. PubMed PMID: WOS:A1994NZ79300008.
2. TS I, Y Z, N K, SB R, T Z, S W, J K, editors. 20-To-8 Channel Tx Array with 32-Channel Adjustable Receive-Only Insert for 7T Head Imaging. International Society of Magnetic Resonance in Medicine; 2013; Salt Lake City, Utah.
3. Santini TK, Narayanan; Wood, Sossena; Raval, Shailesh; Zhao, Yujuan; Fischetti, Anthony; Koo, Minseok; Aizentein, Howard; Ibrahim, Tamer, editor. 64-channel Double-Octagon Tx Head Coil for 7T Imaging. In Proc of the 25th International Society of Magnetic Resonance in Medicine Annual Meeting; 2017; Honolulu, Hawaii, USA.
Figures