4392
About the Ideal Receive Array for Human Head MRI1High-Field MR Center, Max Planck Institute for Biological Cybernetics, Tuebingen, Germany, 2Institute of Physics, Ernst-Moritz-Arndt University, Greifswald, Germany
Synopsis
For the first time, we present a systematic framework to assess the intrinsic SNR performance of loop-only and dipole-only receive arrays in a realistic human head model. Thereby, we distribute generic current patterns on a helmet-like and a cylindrical coil holder. These current patterns form a basis set for any kind of receive element one could place on the holder. We demonstrate how to design an ideal receive array for human head applications by using complementary current patterns.
Purpose
During the last twenty years, loop-only receive arrays have become the gold-standard for human head NMR at low fields (B0 = 1.5 T and 3 T). At ultra-high fields (B0 ≥ 7 T), the electric dipole moved into focal interest within the past five years. There were initial studies with dipole-only arrays (1-4) but also with a combination of loop and dipole elements (5-7). Moreover, vertical loop elements were combined with surface loops (8). The purpose of this study was to do a systematic investigation to what extent loop- and dipole-only receivers are able to reach the ultimate SNR threshold in a realistic human body model and how a combination of the two complementary coil element types could enhance the SNR.
Methods
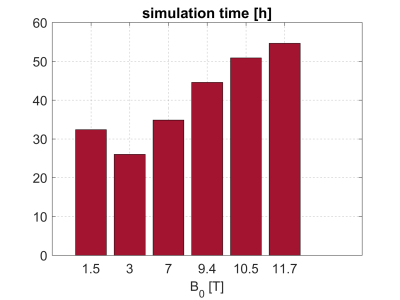
We investigated the SNR performance of loops and dipoles at different field strengths (B0 = 1.5 T, 3 T, 7 T, 9.4 T, 10.5 T, 11.7 T). During the whole study protons were assumed as the NMR visible isotope. We distributed generic current patterns, which are able to represent any kind of loop or dipole element, on two commonly used coil holder geometries: First, we used a spherical cap (Fig.1a) and evaluated the ultimate SNR within the framework introduced in (9). Next, we calculated the best possible SNR achievable with either divergence-free current patterns (loop-only arrays) or curl-free current patterns. We also distributed curl- and divergence-free current patterns around a cylindrical surface (Fig. 1b). This allowed us to access the SNR performance of z-directed current patterns (dipole-only arrays). To solve the electromagnetic field problem, we developed a new approach (figure 2). Thereby, curl- and divergence-free surface current patterns KE and KM excited eigenfunctions of the spherical or cylindrical Helmholtz operator. Applying dyadic Green's function theory (10), we could calculate the free-space fields of the current modes. These fields were fed into a fast-volume integral equation solver (11) to obtain the electromagnetic fields in the presence of the realistic body model. We used "Duke" from the virtual family (12) with 2 mm isotropic resolution and 77 different tissue types.The overall fields were stored in a database to create a basis set. For the spherical cap, the basis set consisted of 2550 basis vectors, whereas the cylindrical basis set comprised 3038 vectors.The numerical field computation of scattered fields was the computational bottleneck and was done on a high performance GPU accelerated (NVIDIA Tesla P100) server. Simulation times for creating the spherical cap basis set are shown in figure 3.
Results
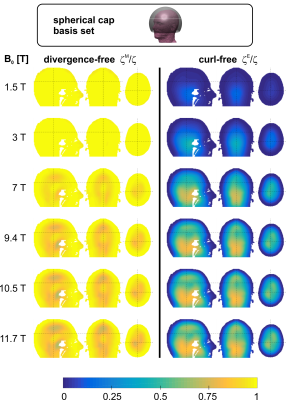
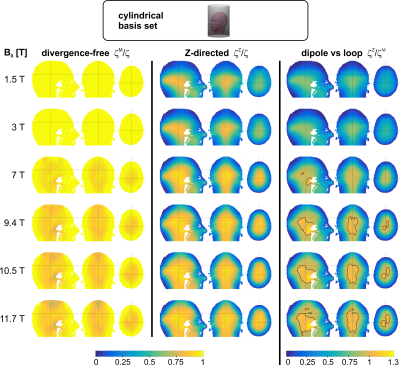
Figure 4 visualizes the SNR performance of divergence-free (ζM/ζ) and curl-free (ζE/ζ) receive arrays on a helmet-like coil holder at various field strenghts. At low field (B0=1.5 T and 3 T), loop-only arrays capture more than 90% of the ultimate SNR limit in the entire human head. Contrasting, at ultra-high field strength, loop-only receivers are not able to reach the ultimate SNR threshold everywhere in the head. At positions of lower ζM/ζ, adding dipole elements to the loop array substantially improves the SNR. The maximum SNR increase when using both element types is about 19% at 7 T and 31% at 9.4 T. Regarding the cylindrical coil holder (figure 5), the SNR of loop-only arrays can be boosted by maximally 17% (7 T) and 25% (9.4 T). Dipole-only arrays have their highest SNR performance in central regions of the human head, but are not very efficient in the periphery. Above 7 T, they capture 93% of the ultimate SNR in central head regions. A direct SNR comparison between loops and dipoles on a cylindrical former reveals, that at 9.4 T and above, dipoles outperform loops at central head regions. At those locations, dipole-only arrays result in about 24% higher SNR than loop-only receivers.Discussion
We have shown, that at ultra-high fields, adding complementary current patterns to loop-only receivers can substantially improve the SNR at specific locations in the human head. Regarding a cylindrical coil holder, loops can be complemented by straight, z-directed dipoles. There have been a few studies to combine loops and dipoles (5-7). On a helmet-like holder, loops could be complemented by ϑ-directed dipoles, which were introduced in (3). Another possibility for complementing divergence-free current patterns is to use vertical loop elements. Promising results were demonstrated in (8).Conclusion
For the first time, we have presented a systematic framework to assess the intrinsic SNR limits of loop-only and dipole-only receive arrays. We have shown how to design an ideal receive array by using complementary current patterns. Our framework is also useful to extract ideal current patterns yielding the ultimate SNR.Acknowledgements
We thank the authors of the MARIE solver package Prof. Athanasios Polimeridis, Dr. Jorge Villena and José Serrallés. We are also grateful to Prof. Ralf Schneider and Stefan Kemnitz from the university computer center in Greifswald for the support to set up the GPU server.References
(1) Lagore RL, DelaBarre L, Tian J, Adriany G, Eryaman Y, Vaughan JT. End-loaded dipole array for 10.5T head imaging. Proceedings of the 24th Annual Meeting of ISMRM, Singapore, Singapore; 2016. p 2138.
(2) Tian J, Lagore R, Delabarre L, Vaughan JT. Dipole array design considerations for head MRI at 10.5T. Proceedings of the 24th Annual Meeting of ISMRM, Singapore, Singapore; 2016. p 3524.
(3) Zhang B, Chen G, Cloos M, Yu Z, Walczyk J, Collins C, Brown R, Lattanzi R,Sodickson D, Wiggins G. 29-channel receive-only dense dipole head array for 7T MRI. Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, USA; 2017. p4314.
(4) Oh C, Lee C, Kumar S, Yoon J, Jeong H, Kim J, Jo Y, Kim J, Bruns C, Herrmann T, Bernarding J, Cho Z. Top-hat dipole RF coil with large field of view for 7 T brain MR imaging. Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, USA; 2017. p 767.
(5) Eryaman Y, Guerin B, Kosior R, Adalsteinsson E, Wald LL. Combined loop + dipole arrays for 7 T brain imaging. Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, USA; 2013. p 393.
(6) Chen G, Lakshmanan K, Sodickson D, Wiggins G. A combined electric dipole and loop head coil for 7T head imaging. Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada; 2015. p 3133.
(7) Woo MK, Lagore RL, DelaBarre L, Lee BY, Eryaman Y, Radder J, Erturk A,Metzger G, van de Moortele PF, Ugurbil K, Adriany G. A geometrically adjustable loop-dipole (LD) head array for 10.5T. Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, USA; 2017. p 1051.
(8) Avdievich NI, Giapitzakis IA, Henning A. Optimization of the receive performanceof a tight-fi t transceiver phased array for human brain imaging at 9.4T. Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, USA; 2017. p 4309.
(9) Pfrommer A, Henning A. The ultimate intrinsic SNR in a spherical phantom with regard to an open-pole surface current distribution at 9.4T. Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, USA; 2017. p 749.
(10) Tai CT. Dyadic Green functions in electromagnetic theory. New York: IEEE Press Series on Electromagnetic Waves; 1994.
(11) Villena JF, Polimeridis AG, Wald LL, Adalsteinsson E, White JK, Daniel L. MARIE - a MATLAB-based open source software for the fast electromagnetic analysis of MRI systems. Proceedings of the 23rd Annual Meeting of ISMRM, Toronto,Canada; 2015. p 709.
(12) Christ A et al. The virtual family- development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010;55:N23-N38.
Figures
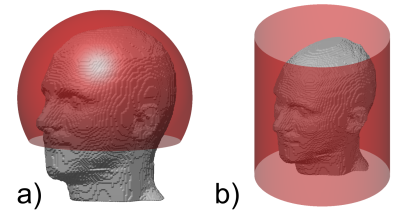
Figure 1: Setup to study the SNR performance of loops and dipoles. Generic current patterns were distributed on a) a spherical cap of radius 13 cm and opening angle of 120°. b) a cylindrical surface of radius 13 cm and length of 30 cm.