4317
Novel crusher coils for elimination of surface MR signals1SIr Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom
Synopsis
There are multiple applications of magnetic resonance imaging and spectroscopy for which it is useful to be able to attenuate the signal that arises from surface structures. Surface signal can be attenuated by using local coils which generate a spatially varying magnetic field that decays rapidly with distance from the surface. In previous work, crushing has been accomplished by using “meander-line” coils which the current flow is predominantly along one dimension. Here we design novel crusher coils in which the current equally flows along two orthogonal directions, and demonstrate via simulations and experiments at 3 T that these coils offer advantages for surface signal crushing.
Introduction
There are multiple applications of magnetic resonance imaging and spectroscopy for which it is useful to attenuate the signal that arises from surface structures. These include MR spectroscopy experiments where contaminating signals from superficial fat or skeletal muscle are problematic [1-3] and experiments where attenuation of strong signals arising near to surface RF coils is required[4-6]. Surface signal can be attenuated by using local coils which generate a spatially varying magnetic field that decays rapidly with distance from the surface. In previous work, crushing has been accomplished by using “meander-line” coils[1-6] in which current flow is predominantly along one dimension. Here, by exploiting insight into the forms of field variation allowed by Maxwell’s equations, we design novel crusher coils in which the current flows along two orthogonal directions, and demonstrate that these coils offer advantages for surface signal crushing.Theory
Crushing the surface signal requires the application of a magnetic field $$$\textbf{b}(\textbf{r})$$$, in which the grad of the field component that is parallel to B0 decreases with depth (see Figure 1). Simple analysis, shows that this condition can only be fulfilled by a magnetic field that varies periodically with x and y, and exponentially with z, taking the form
$$\textbf{b}(\textbf{r})=b(\alpha \sin(\alpha x)\cos(\beta y)\textbf{i}+\beta \cos(\alpha x)\sin(\beta y)\textbf{j}+\sqrt{\alpha^{2}+\beta^{2}}\cos(\alpha x)\cos(\beta y)\textbf{k})e^{-\sqrt{\alpha^{2}+\beta^{2}}z} [1]$$
A current distribution $$$\textbf{J}(x,y)=\triangledown S\times\textbf{k} $$$, confined to the z=0 plane with
$$S(x,y)=\frac{b}{\mu_{0}} \cos(\alpha x)\cos(\beta y)[2]$$
will generate this field.
For meander-line coils, $$$\beta \simeq 0$$$ so that $$$\textbf{b}(\textbf{r})=b \alpha( \sin(\alpha x)\textbf{i}+\cos(\alpha x) \textbf{k})e^{-\alpha z} $$$ and with this arrangement the efficiency of crushing depends strongly on the orientation of the current distribution with respect to the B0-field. Orientation-dependence can be reduced by using a coil in which the current varies with both x and y.
Setting $$$\beta = \alpha $$$ yields
$$\textbf{b}(\textbf{r})=b\alpha ( \sin(\alpha x)\cos(\alpha y)\textbf{i}+\cos(\alpha x)\sin(\alpha y)\textbf{j}+\sqrt{2}\cos(\alpha x)\cos(\alpha y)\textbf{k})e^{-\sqrt{2}\alpha z} [3]$$
which has a faster decay with depth than the 1D case and produces a greater degree of crushing at fixed b, $$$\alpha $$$ and depth attenuation. The resulting stream function yields a coil composed of an array of square fingerprint elements, of side $$$\frac{\pi }{ \alpha}$$$, in which the sense of current circulation is reversed in adjacent elements (Fig. 2). For this arrangement, the maximum gradient of the relevant field component takes a value between $$$2 b \alpha ^{2} e^{-\sqrt{2}\alpha z}$$$ (B0 along z) and $$$\sqrt{2} b \alpha ^{2} e^{-\sqrt{2}\alpha z}$$$ (B0 perpendicular to z). The value of $$$\alpha$$$ which minimises the power dissipated (or energy stored) in the array per unit gradient (at depth zd) squared is found to be $$$\frac{3 }{ 2 \sqrt{2} z_{d}}$$$.
Methods
A 4x4 element coil with 5 windings per element was designed to generate a crushing gradient optimised for depth zd=1.5 cm: coil elements were each 4.44 cm ($$$\alpha$$$= 1 cm-1) in side (Fig. 2). The coil was wound on a Perspex sheet using 0.23 mm diameter copper wire (R = 3.7 Ω; L=16μH). A similar 3x3 coil with elements offset by 2.22 cm in both x and y relative to the 4x4 coil was also constructed on the reverse side of the Perspex sheet. Experiments were carried out on a 3T scanner with the crusher coils driven with a continuous current of 65mA using a lead-acid battery. Field maps were acquired using a dual-echo GE sequence with the crusher coil adjacent to a water filled phantom. Short (3ms) and long (50ms) TE gradient echo images were also acquired from the phantom and a human subject to demonstrate the signal crushing capability of the coil.Results
Figure 3a&b show the field variation measured in a coronal plane ~8 mm from the crusher coil. Figure 3c shows that the logarithm of amplitude of field modulation varies linearly with z with 1 cm-1 slope, as expected. Field maps acquired with the array at different angles to B0 confirmed that the field variation was well described by Eq. [3]. Figure 4a&b show sagittal images acquired from the phantom with short and long TE, demonstrating that signal is crushed near the array when the spatial variation of the induced phase is large. More uniform crushing can be achieved by using the two crusher coils in combination as shown in Fig. 4c. Figure 5 shows that good local crushing of the signal from the surface fat layer in the human thigh can also be achieved.Discussion
A novel crusher coil array has been introduced and tested. These coils produce a magnetic field whose Cartesian components all vary with spatial position (in contrast to meander-line coils), thus reducing the orientation dependence of crushing efficacy.Acknowledgements
HE received an EPSRC Vacation Bursary.References
1. Chen, W. and J.J. Ackerman, Spatially-localized NMR spectroscopy employing an inhomogeneous surface-spoiling magnetic field gradient. 1. Phase coherence spoiling theory and gradient coil design. NMR in biomedicine, 1990. 3(4): p. 147-57.
2. Boer, V.O., et al., Lipid suppression for brain MRI and MRSI by means of a dedicated crusher coil. Magnetic Resonance in Medicine, 2015. 73(6): p. 2062-2068.
3. Schaller, B., et al., Suppression of skeletal muscle signal using a crusher coil: A human cardiac (31)p-MR spectroscopy study at 7 tesla. Magnetic Resonance in Medicine, 2016. 75(3): p. 962-972.
4. Crowley, M.G. and J.J.H. Ackerman, ENHANCED SURFACE-COIL SPATIAL LOCALIZATION WITH AN INHOMOGENEOUS SURFACE GRADIENT. Journal of Magnetic Resonance, 1985. 65(3): p. 522-525.
5. Jehenson, P. and G. Bloch, ELIMINATION OF SURFACE SIGNALS BY A SURFACE-SPOILING MAGNETIC-FIELD GRADIENT - THEORETICAL OPTIMIZATION AND APPLICATION TO HUMAN INVIVO NMR-SPECTROSCOPY. Journal of Magnetic Resonance, 1991. 94(1): p. 59-72.
6. Wiesler, D.G., et al., Reduction of field of view in MRI using a surface-spoiling local gradient insert. JMRI-Journal of Magnetic Resonance Imaging, 1998. 8(4): p. 981-988.
Figures

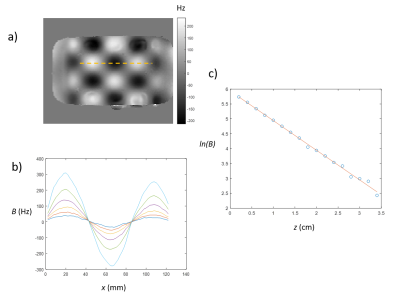
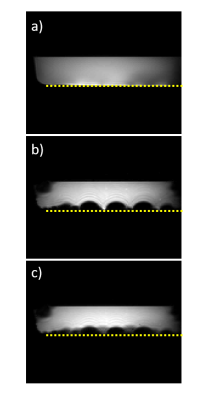

Figure 5. Axial gradient echo images with TE= 40 ms and 3 mm isotropic resolution acquired from the upper thighs of a healthy volunteer. The crusher coil was placed underneath the left leg. (a) No current in the crusher coil; (b) Arrow indicates local attenuation of the surface fat layer produced with 67 mA in the coils.