4313

B1 vector field mapping through multi-orientation B1+ measurements

Seung-Kyun Lee^1,2 and Sukhoon Oh³

¹Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Republic of Korea, ²IBS Center for Neuroscience Imaging Research, Suwon, Republic of Korea, ³Bioimaging Research Team, Korea Basic Science Institute, Cheongju, Republic of Korea

Synopsis

We present theory and experimental validation of reconstruction of all three components of RF vector magnetic field (B1 vector) in MRI. Using eight-orientation B1+ magnitude mapping, the magnitudes and relative phases of all Cartesian components of B1 vector can be unambiguously determined. The method is demonstrated on a phantom in a birdcage transmit coil with a standard B1+ mapping sequence at 3T. Our method can be used to validate assumptions in MR-based electrical properties tomography (MR-EPT) and specific absorption rate (SAR) modeling.

Introduction

Increased tissue-RF field interactions at ultra-high-field MRI presents challenges in two ways: image shading and tissue heating. While the former involves only one (proton co-rotating) component of the RF field ($$$B_1^+$$$), heating is contributed by all three components of the RF vector magnetic field (B₁ vector) through induction of an electric field. Experimental measurement of the B₁ vector field is therefore relevant to modeling specific absorption rate (SAR) in high-field MRI. Also, MR-based electrical properties tomography (MR-EPT)^1,2 could benefit from additional B₁ field information. While conventional B₁ mapping only measures $$$B_1^+$$$, Florian et al.³ noted in 2006 that other B₁ components could be accessed by multi-orientation measurements. Here, we present a theory of B₁ vector field mapping from multi-orientation scans, and provide experimental validation through phantom measurements and RF field simulations.

Theory

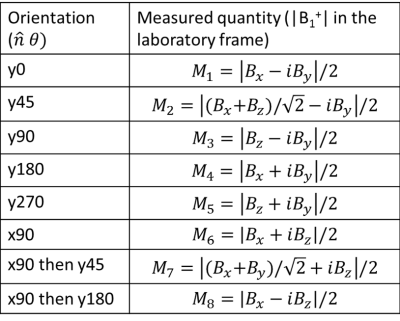
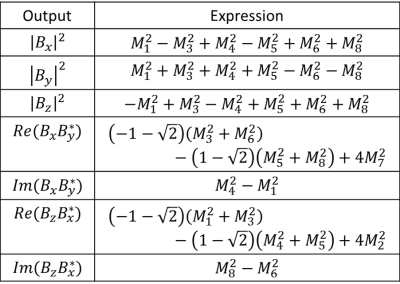
We will assume that the RF transmitter is small enough compared to the scanner’s RF shield that the B₁ field of interest is not significantly affected by the shield. Accordingly, we define an “RF system” as the transmitter and the object being scanned with their relative positions fixed. We aim at finding the B₁ components $$$(B_x, B_y, B_z)$$$ in the RF system before rotation. Conventional $$$B_1^+$$$ mapping only measures $$$B_{1,orig}^+ = |B_x – iB_y|/2$$$. If we now rotate the RF system by ϑ around an axis $$$\hat{n} = (n_x,n_y,n_z)$$$, the B₁ vector in the magnet’s reference frame becomes $$$\vec{B}_{1new} = R(\hat{n},\theta) \vec{B}_{1orig}$$$, where $$$R$$$ is a rotation matrix. The corresponding new, measureable $$$B_1^+$$$ magnitude is given by $$ |B_{1,new}^+|=|(\cos\theta-in_z\sin\theta)(B_x-iB_y) +B_z(n_y+in_x)\sin\theta + \vec{B}\cdot\hat{n}(n_x-in_y)(1-\cos\theta)|.$$ Multiple-orientation measurements of the above quantity can allow disentangling of magnitudes and relative phases of $$$(B_x, B_y, B_z)$$$. Many multi-orientation strategies can be devised, balancing mathematical complexity and experimental practicality. Here we present an 8-orientation method which involves large angles but allows mathematically straightforward solution. The relevant equations are summarized in Tables 1-2.

Methods

Experiment

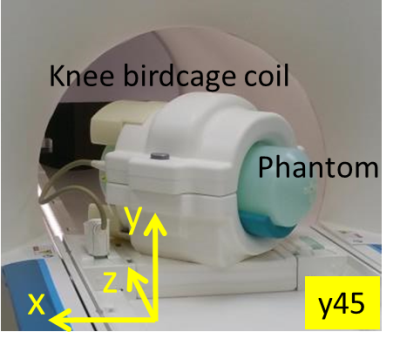
$$$B_1^+$$$ maps on a cylindrical phantom were acquired in a 3T whole-body scanner (Magnetom Prisma, Siemens Healthineers, Germany) with a vendor-provided extremity (knee) coil, consisting of 1 quadrature (birdcage) transmit coil and 15 receive elements. A vendor-provided fast $$$B_1^+$$$ mapping sequence⁴ was applied to each of the eight orientations to produce a set of 2D $$$B_1^+$$$ maps on the phantom’s axial plane. During prescription, scan planes were rotated to follow the phantom orientation. The phantom was a cylinder with length (flat part) = 42 cm and diameter = 14.4 cm, consisting of aqueous solution of NaCl and NiSO₄, as provided by the vendor. The acquired $$$B_1^+$$$ maps were processed according to Tables 1-2 to calculate the magnitudes and relative phases of the RF-frame components of B₁.

Simulation

The RF fields were simulated in XFdtd v7.6 (Remcom, USA) on the following model: high-pass birdcage coil with 12 rungs, diameter/length = 20/20 cm, frequency = 123.25 MHz; an axially located cylindrical phantom with σ=1 S/m, ε_r=78, length/diameter = 42/14.4 cm. The effect of an RF shield was tested and found to affect B₁ field by less than 4% at tested orientations.

Results

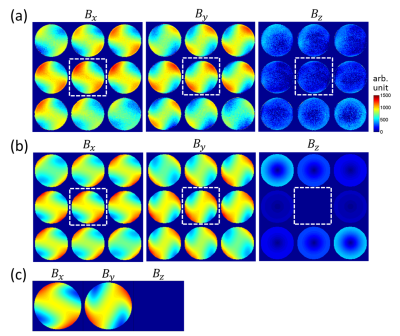
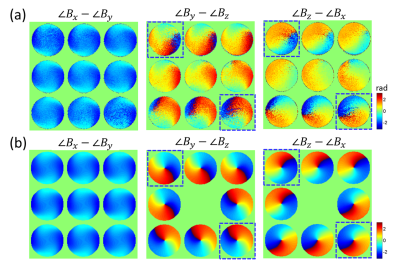
Figure 2 shows the magnitudes of $$$(B_x,B_y,B_z)$$$ reconstructed from experimental data in comparison with simulation. The successive slices are 18 mm apart. The agreement is generally good. The results on the middle slice also agreed well with analytical solutions for an infinitely long cylinder⁵. Small differences between the experimental and simulated data can be partly attributed to asymmetric positioning of the phantom inside the coil, which was visible in localizer scans (not shown). Our data show the spatial inhomogeneity of the linear components of the transverse B₁ field at 3T, and how B_z grows towards the end of the birdcage coil. In the relative phase maps (Fig. 3), the phase of B_y is about π/2 ahead of B_x, consistent with left circular polarization. B_z phase is sensitive to experimental (positioning) errors due to small B_z magnitudes. Measured relative phases involving B_z resemble simulation better on the end slices where B_z is stronger.

Discussion

To our knowledge this is the first experimental demonstration of RF vector field mapping (up to a common phase) in MRI. Our method could inform MR-EPT methodology and SAR modeling. Extension of the method to in-vivo studies obviously requires reduction of the rotation angles as well as streamlining of multi-orientation scan workflow. Given existing literature on multi-orientation human scans for susceptibility⁶ and $$$B_1^-$$$ mapping⁷, we do not think this is an insurmountable problem. Future research directions include development of human study-compatible scan protocols and absolute phase determination through additional phase mapping or theoretical constraints.

Acknowledgements

This work was supported by IBS-R015-D1.

References

(1) Zhang X. et al., IEEE Rev Biomed Engineering 7:87-96 (2014)

(2) Katscher U. et al., NMR in Biomed (2017) DOI: 10.1002/nbm.3729

(3) Wiesinger F. et al., Prospects of absolute B1 calibration, in Unsolved Problems and Unmet Needs in MR, 14th Annual Meeting of ISMRM (2006).

(4) Fautz H.P. et al., B1 mapping of coil arrays for parallel transmission, 16th Annual Meeting of ISMRM (2008), Abstract 1247.

(5) Glover G.H. et al., J Magn Res 64:255-270 (1985)

(6) Liu T. et al., Magn Res Med 61:196-204 (2009)

(7) Lee S-K. and Dixon, W.T., 19th Annual Meeting of ISMRM (2011), Abstract 4429.

Figures

Table 1. Measured quantities in an eight-orientation B1+ mapping experiment

Table 2. Seven outputs to determine the magnitudes and relative phases of the Cartesian components of the B1 vector in the RF reference frame, expressed in terms of the measured quantities. Only two of the three relative phases are independent.

Figure 1. Experimental setup showing one of the eight orientations of the RF system (=transmit coil plus the phantom). The coordinate axes indicate the laboratory frame coordinates.

Figure 2. Measured (a) and simulated (b) B1 vector field maps on nine slices of a cylindrical phantom. The dashed square indicates the middle slice. Slice ordering is from top left (-z) to the bottom right (+z), going first from the left to the right. Analytical B1 maps for an infinitely long cylinder are shown in (c), which agree well with the middle-slice results.

Figure 3. Measured (a) and simulated (b) relative phases of the components of the B1 vector field. Blue dashed squares indicate end slices where the agreement between the data and simulation is reasonable for phases involving Bz (last two columns).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

4313