4311
Bloch-Siegert Shift Based Method for Mapping $$$B_1^+$$$ Magnitude of Arbitrary Multi-Transmit RF Configurations1Centre for Functional and Metabolic Mapping, The University of Western Ontario, London, ON, Canada, 2Department of Medical Biophysics, The University of Western Ontario, London, ON, Canada
Synopsis
Mapping B1+ magnitude fields for any arbitrary RF-configuration of interest is desirable and often required in parallel multi-transmit systems. Conventional mapping methods work by taking either the magnitude ratio or the phase difference of MRI images, and thus they fail in regions of low MRI-signal which can easily occur for an arbitrary RF-configuration. We propose a new BSS based method which always uses the CP-mode for excitation while the RF-configuration of interest is used only for the off-resonance RF-pulse. Through this approach, the proposed method works even if the RF-configuration of interest has very-low magnitudes within the imaging volume.
Introduction
Parallel-transmit (pTx) systems consisting of RF-coil arrays bring in the possibility of tailoring $$$B_1^+$$$ field by configuring the magnitude and phase of each coil element (RF-configuration). These systems can be used for mitigating $$$B_1^+$$$ inhomogeneity and for accelerating multidimensional excitation RF pulses. For any arbitrary pTx RF-configuration, $$$B_1^+$$$ field distribution is required for $$$B_1^+$$$ shimming, design and development of pTx coils, and SAR estimation. Several $$$B_1^+$$$ magnitude mapping methods have been previously developed1,2,3 However, since these methods work by taking either the magnitude ratio or the phase difference of MRI images, they suffer in regions of low MRI-signal which can easily occur for an arbitrary RF-configuration. In this study, we propose a Bloch-Siegert Shift (BSS) based method which is capable of measuring $$$B_1^+$$$ field even in the mentioned null regions.Theory
In traditional BSS method, an off-resonance RF pulse (OffRFP) ($$$\Delta f>2$$$kHz) is applied right after the excitation RF pulse (ExcRFP) and then the signal is read out using a GRE sequence. The OffRFP does not excite spins but, considering the effective-B1 field theory, it acts as an additional B-field applied in the z-direction which causes phase shift in the transverse spins given by3 $$\phi _{BSS} =\int_{0}^{T}\frac{(\gamma B_1(t))^2}{2\Delta f}dt$$ where $$$B_1(t)$$$, $$$\Delta f$$$, and $$$T$$$ are the envelope, frequency shift and the duration of the OffRFP. To calculate $$$\phi _{BSS}$$$, the phase difference is taken between two scans acquired with positive and negative frequency shifts.
As mentioned above, the BSS method fails in the null regions of arbitrary RF-configurations due to the inaccuracy of the phase in these regions. To overcome this problem, we propose the use of two different RF-configurations for the ExcRFP and OffRFP: For the excitation RF pulse, we use only the CP-mode of the coil, obtained by a one-time optimization of the $$$B_1^+$$$ homogeneity for an average head, which gives high-signal in all regions. As for the OffRFP, we use the RF-configuration of interest for which we want to map $$$B_1^+$$$ field.
Methods
All scans were conducted on a Siemens 7T MRI scanner (Erlangen, Germany) equipped with a pTx system of 8 transmit and 32 receive channels. The manufacturer’s GRE sequence is modified to fulfill the BSS pulse sequence. Axial 2D brain images and corresponding $$$B_1^+$$$ maps are acquired with the following parameters for two volunteers: TR 600 ms, TE 12 ms, FOV 240x240(128x128) mm, flip angle 60 degree, OffRFP with a Fermi shape ($$$\Delta f=4$$$kHz, $$$T=8$$$ms, nominal peak 5.8uT). Discrete Fourier transform matrix coefficients were used to obtain 8 different RF-configurations4. For Subject 1, these configurations were applied both to the ExcRFP and OffRFP (traditional BSS method). For Subject 2, the configurations were applied only to the OffRFP and, for ExcRFP, the CP-mode was always used (proposed BSS method).Results and Discussion
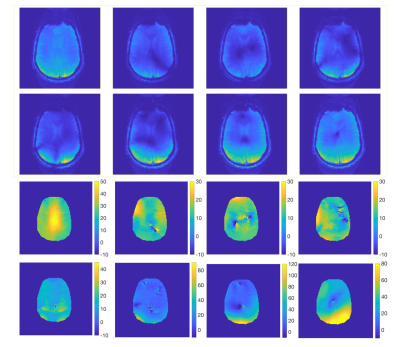
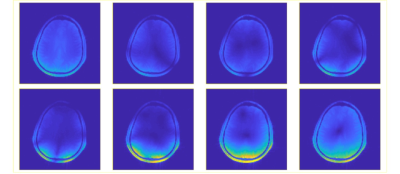
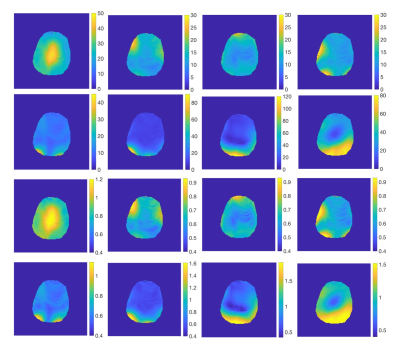
Figure 1 shows the MRI magnitude and phase difference images for Subject 1 for which the traditional BSS method was used. The null regions are apparent in magnitude images except in the first RF-configuration which corresponds to CP mode excitation. In null regions, the phase difference is distorted and thus the traditional BSS method fails. Figure 2 shows the MRI magnitude image for Subject 2. Since the excitation RF-configuration is always the CP-mode, the same MRI magnitude images are obtained for all 8 RF-configurations. Figure 3 shows additional magnitude images which are acquired with the FLASH sequence to show null regions for the different RF-configurations. Figure 4 shows the phase difference and $$$B_1^+$$$ magnitude images for the different configurations. In contrast to the case where the RF-configurations were the same for the ExcRFP and OffRFP, the phase difference images show no sign of distortion in null regions. Therefore, we were able to apply the proposed BSS method and get $$$B_1^+$$$ magnitude maps for each configuration.Conclusion
Mapping $$$B_1^+$$$ magnitude fields for any arbitrary RF-configuration is desirable and often required in pTx systems. For this purpose, we propose a new BSS based method which always uses the CP-mode for ExcRFP while the RF-configuration of interest is used only for the OffRFP. Through this approach, the excitation and mapping processes are separated, allowing the proposed BSS method to work even if the RF-configuration of interest has very-low magnitudes within the imaging volume. Another important feature of the method is that the acquired $$$B_1^+$$$ magnitude maps have the same noise characteristics in all regions since these maps are always obtained by using MRI signal resulting from CP-mode excitation. We believe this method can be a useful tool for the design, development and verification of pTx systems.Acknowledgements
This work was supported by The Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant to Ravi Menon.References
1. Cunningham CH, Pauly JM, Nayak KS. Saturated double-angle method for rapid B1+ mapping. Magn. Reson. Med. 2006;55(6):1326–1333
2. Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 2007;57(1):192–200.
3. Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 2010;63(5):1315–1322.
4. Nehrke K, Börnert P. Eigenmode analysis of transmit coil array for tailored B1 mapping Magn. Reson. Med. 2010;63(3):754–764
Figures