4268

High-dimensional and accurate dictionary fitting with B-spline interpolation and gradient-based optimization
Willem van Valenberg1,2, Stefan Klein2, Frans M. Vos1,3, Lucas J. van Vliet1, and Dirk H.J. Poot1,2

1Quantitative Imaging Group, Delft University of Technology, Delft, Netherlands, 2Biomedical Imaging Group, Erasmus Medical Center, Rotterdam, Netherlands, 3Department of Radiology, Academic Medical Center, Amsterdam, Netherlands

Synopsis

Dictionary matching in MR fingerprinting acquisitions quantifying many parameters, such as T1 T2, T2’, B0, B1+, and PD, becomes prohibitively expensive due to the dense grid in each dimension of the dictionary that is required. In this work we propose B-spline interpolation of the dictionary to reduce the dictionary size and to enable efficient nonlinear least-squares fitting by gradient-based optimization methods. The experiments show that the method substantially reduces fitting error, especially when the SNR is high and dictionary resolution is the limiting factor for improving the precision of the quantitative parameters.

Introduction

MR Fingerprinting (MRF) methods combine a pseudorandom acquisition with undersampling and dictionary-based fitting to create multi-parametric maps in a clinical scan time [1]. The dictionary contains the expected signal for different combinations of parameter values (e.g. $$$T_1, T_2, T_2’, PD, \Delta B_0, B_1^+$$$). The MRF acquisition encodes all these parameters into the MR signal. However, creating a dictionary with sufficient steps in each parameter dimension to fit with high precision quickly becomes infeasible due to the curse of dimensionality. In this work, we present a framework for fitting the MRF signal through B-spline interpolation of the dictionary, in combination with a gradient-based local optimization routine. Interpolation is justified because the dictionary smoothly varies with the underlying parameters. The compact support of the B-spline and its separability enable highly efficient interpolation and gradient calculation, even in high-dimensional (in this work 5D) spaces

Methods

The dictionary interpolation is tested on the original MRF pulse sequence (Fig 1C of [1]). Bloch simulation of this sequence determines the dictionary atoms. The pulse sequence is described by an event-based model with interchanging periods of relaxation and instantaneous events: RF pulses, gradient spoiling and signal sampling. The parameter values form a five-dimensional grid as discretized in Table 1. For each combination the signal is simulated by 1006 spins with shared longitudinal, $$$T_1$$$, and transversal, $$$T_2$$$, relaxation times, proton density, $$$PD$$$, initial phase, $$$\varphi_0$$$, and RF pulse scaling $$$B_1^+$$$. The intravoxel dephasing, $$$T_2’$$$, and static field inhomogeneity, $$$\Delta B_0$$$, are simulated by sampling the off-resonance frequency of each spin from a Cauchy distribution of scale $$$T_2’$$$ around $$$\frac{\gamma}{2\pi} \Delta B_0$$$. Proton density and initial phase lead to a (complex) multiplication of the signal that we determine without discretization.

Conventionally, the measured MRF signals are matched to the dictionary atom with maximal inner product [1]. As the parameter resolution equals the dictionary resolution, each dimension requires many atoms to obtain precise parameter maps. Since the number of dictionary atoms scale the computation time for both dictionary generation and matching, this quickly becomes infeasible.

We propose to increase the accuracy of our parameter maps by interpolating the dictionary using B-splines [2], and subsequently fitting the signal using efficient gradient-based optimization. The $$$n$$$-order B-spline kernel gives an interpolation error that scales with $$$\mathcal{O}(\Delta p^{n+1})$$$ and a calculation time that scales as $$$\mathcal{O}((n+1)^d)$$$ [3], where $$$\Delta p$$$ and $$$d$$$ are the grid spacing and the parameter space dimension. Note that $$$n=0$$$ and $$$n=1$$$ are equivalent to nearest-neighbor interpolation (i.e., dictionary matching) and linear interpolation. Each parameter dimension is extended by two atoms on each side to reduce boundary effects. A signal prediction function returns the spline interpolated signals for a given position in the dictionary. For a given signal, the parameters are estimated with a non-linear least-squares method minimizing the difference between interpolated and given signal, starting from the conventional dictionary match. The employed optimization uses the gradients of the spline function, as they can be computed very efficiently using a recursive implementation exploiting the separability of the B-spline kernel [3].

To determine the accuracy of the spline interpolation over the dictionary range, we generate 1000 test objects with parameter values randomly sampled from the ranges given in Table 1, and $$$PD:= 1$$$ and $$$\varphi_0 \in[-\pi,\pi]$$$ rad. Complex Gaussian noise is added to simulate different SNRs (root-mean-square over the signals divided by noise standard deviation). We fit each test object using spline orders 0, 1, and 2 and compare the fit error for each parameter.

Results

Figure 1 shows for each of the 1000 test signals the relative error of the relaxation times as function of $$$T_1, T_2, T_2’$$$ for $$$n=0,1,2$$$. Figure 2 shows the errors in $$$\Delta B_0, B_1^+$$$, and $$$\varphi_0$$$ for $$$n=0,1,2$$$. Both figures show that interpolation substantially reduces the error. Figure 3 shows the mean relative errors and mean absolute errors as function of SNR for $$$n=0,1,2$$$. For SNR>3 linear interpolation has lower error than dictionary matching with this selected dictionary atom spacing. For SNR>10, $$$n=2$$$ improves over linear interpolation. Note that these specific thresholds depend on the spacing between dictionary atoms.

Discussion

For SNR levels found in practice, the presented method improves the precision of each tested parameter mapping. For each parameter except $$$\Delta B_0$$$, a small number of dictionary atoms can accurately approximate the whole dictionary range.

Conclusion

B-spline interpolation in combination with gradient-based optimization improves the precision of parameters estimated in MRF. The proposed fitting approach can directly replace the dictionary matching step in any MR fingerprinting reconstruction method. Hence it can be used to significantly reduce dictionary size.

Acknowledgements

No acknowledgement found.

References

1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature 2013;495:187–192. doi: 10.1038/nature11971.

2. Unser M. Splines: A perfect fit for signal and image processing. IEEE Signal processing magazine 1999;16:22–38.

3. Huizinga W, Klein S, Poot DHJ. Fast Multidimensional B-spline Interpolation Using Template Metaprogramming. In: Biomedical Image Registration. Lecture Notes in Computer Science. Springer, Cham; 2014. pp. 11–20. doi: 10.1007/978-3-319-08554-8_2.

Figures

Table 1: Discretization of the parameter dimensions in the dictionary.

Figure 1: Comparison of the relative error between the fitted relaxometry values and the true values for different spline interpolation orders. RMS indicates the root mean square over the relative errors. The SNR equals 10000.

Figure 2: Comparison of the absolute error between the fitted parameter values and the true values for different spline interpolation orders. RMS indicates the root mean square over the absolute errors. The SNR equals 10000.

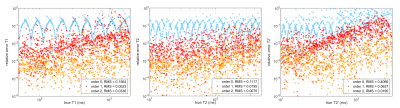
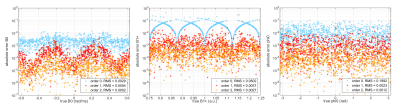
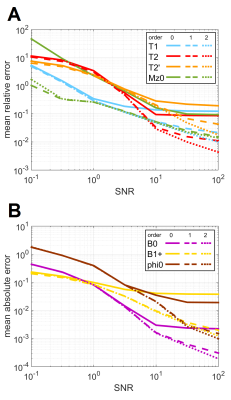
Figure 3A: Mean relative error in T1, T2, and T2' over the test set as function of SNR level and for different spline orders.

Figure 3B: Mean absolute error in B0, B1+, and φ0 over the test set as function of SNR level and for different spline orders.



Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4268