4267
Bloch-Torrey Simulation to Quantify Diffusion Effects on Multi-Parametric Sequences with Application for MR Fingerprinting1Mathematics, Tel Aviv University, Tel Aviv, Israel, 2Sagol School of Neuroscience, Tel Aviv university, Tel Aviv, Israel, 3Biomedical engineering, Tel Aviv University, Tel Aviv, Israel, 4Center for Advanced Imaging Innovation and Research, New York University, New York, NY, United States, 5Psychiatry and Radiology, Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
Quantifying the effect of self-diffusion on multi-parametric sequences, such as those used for Magnetic Resonance Fingerprinting (MRF) is important to increase the accuracy of dictionary based parameter estimation. To quantify diffusion, we propose a signal simulation approach, which replaces the Bloch equation with the Bloch-Torrey equation, and accounts for protocol and scan dependent parameters. We apply this framework on a Multi Spin Echo (MSE) protocol and quantify the diffusion encoding introduced by the spoiler gradients in this sequence. We further show that increasing the spoiler strength would allow detecting diffusion by including the diffusion effect in the dictionary.
Introduction:
Self-diffusion is one of the factors influencing the accuracy of parameter estimation, especially $$$T_2$$$ relaxation, from many multi-parametric sequences such as those used for Magnetic Resonance Fingerprinting (MRF) [1]. Signal predictions accounting for diffusion properties are thus important to increase accuracy, but also may lead to building dictionaries allowing the simultaneous extraction of diffusion properties and relaxation parameters. Prediction and simulation are, however, complicated especially for pulse sequences in which there is not an analytical solution for diffusion effects. In most MRF schemes the dictionary is predicted using extended-phase-graph estimations [2-3]. We propose to use a numerical simulation to estimate the Bloch-Torrey (BT) equation [4]. The aim of this work is to provide a general platform for the inclusion of diffusion, which can also account for restricted diffusion [5], and for any pulse structure. We demonstrate the effect of diffusion on the measurements of $$$T_2$$$ using a CPMG Multi Spin Echo (MSE) sequence [6]. This sequence uses spoiler gradients to increase precision, however, the spoiler gradients may introduce diffusion effects [7]. Here we apply the BT simulation to quantify the diffusion effects caused by the spoilers and to build dictionaries including both $$$T_2$$$ and diffusion.Methods:
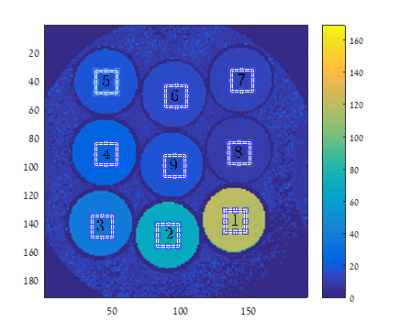
The dynamics of the magnetization $$$\boldsymbol{M}$$$ as a result of diffusion and relaxation, for the exact pulse profile produced by the MRI scanner, without neglecting its time structure, is modeled using the BT equation: $$\frac{\partial\boldsymbol{M}}{\partial t}=\gamma(\boldsymbol{M}\times\mathbf{H})+D\nabla^{2}\boldsymbol{M}-\frac{M_{x}\hat{\boldsymbol{x}}+M_{y}\hat{\boldsymbol{y}}}{T_{2}}+\frac{\left(M_{0}-M_{z}\right)\hat{\boldsymbol{z}}}{T_{1}}, (1)$$ where $$$H$$$ is the applied magnetic field, $$$\gamma$$$ is the gyromagnetic ratio, $$$T_1$$$ and $$$T_2$$$ are relaxation times, $$$D$$$ is the diffusion coefficient and $$$M_0$$$ is the thermal equilibrium magnetization. Eq. (1) is solved numerically in C++ and MATLAB along the spoiler's direction, to describe magnetization in each voxel, using the finite differences method. The voxel borders were defined with a pseudo periodic boundary condition [8], generalized to account for spatially and time dependent gradient. In addition, similar to [6], the simulation used actual parameters from the scanned pulse-sequence scheme. For free diffusion, as used below, the outcome was a dictionary with 196 values of $$$T_2=5…200[ms]$$$, although in general this method can generate dictionary entries for any diffusion coefficient and $$$T_2$$$ combination. The simulations were applied to generate dictionaries for a MSE sequence with 18 echoes ($$$TR = 1500[ms]$$$, $$$TE =12,24...216[ms]$$$), and spoiler gradients $$$G_{spoiler}=-0.489[\frac{G}{cm}]$$$ with duration $$$1.8[ms]$$$. For comparison, identical MSE data was acquired from a phantom (Fig. 1) composed of nine tubes with different relaxation times [6] on a 3 Tesla whole-body MR system, as well as a Single Spin Echo (SSE) sequence with identical parameters. The simulations were repeated to predict diffusion effects with strong spoilers, for $$$T_2=23[ms]$$$ as in tube number 4 with $$$G_{spoiler}=3.5[\frac{G}{cm}]$$$ and identical duration. The $$$T_2$$$ values were extracted from the SSE data using exponential fit and from the MSE by matching to the dictionaries.Results:
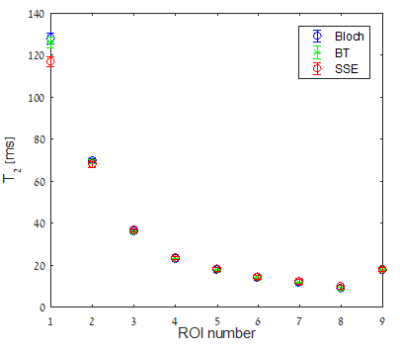
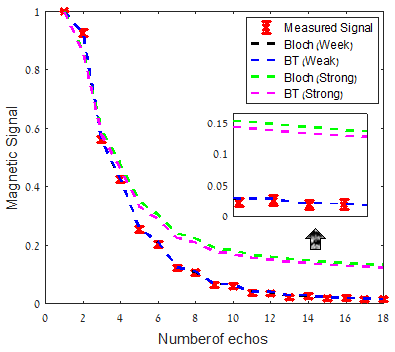
Fig. 2 shows the estimated $$$T_2$$$ values for the nine tubes, when using Bloch and BT dictionaries. The SSE experiment is shown as a reference ground truth. This figure shows that the $$$T_2$$$ estimation was not affected by diffusion in the MSE experiment with weak spoiler gradients. To evaluate the potential of the spoiler to encode diffusion, we simulated the signal with a strong spoiler. Fig.3 compares the signal of the Bloch simulation with the BT simulation. Unlike the weak spoiler case (blue, and black), for the strong spoiler (green and magenta) there is a non-negligible effect of diffusion on the signal. The mean square difference between the simulated Bloch and BT signals was three orders of magnitude larger when the spoiler was strong.Discussion:
By including diffusion in a BT based dictionary, we are able to validate that diffusion did not have much effect on the MSE signal, or on the estimation of $$$T_2$$$, when using weak spoiler gradients. Using our simulations, we show that once the spoiler gradient strength is sufficiently increased quantifiable diffusion effects appear.Conclusions:
We demonstrate a simulation framework that accounts for diffusion effects on any pulse sequence, here demonstrated on a MSE sequence. Applying this simulation for an MSE protocol, modified to use high spoiler gradients, shows promise for the simultaneous encoding of relaxation times and diffusion. While here the spoiler was limited to the z-axis, the MSE sequence as well as our simulation support additional gradient forms that may encode more complex diffusion profiles. It can also be used to extract other parameters such as, $$$T_1$$$, $$$PD$$$ and $$$B_1$$$ , to obtain a better representation of microstructure through a fingerprinting framework.Acknowledgements
NIH R01MH108574; NIH P41EB015902. Dr’s Pasternak and Ben-Eliezer are shared senior authors.References
[1] Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013 Mar 14;495(7440):187-92.
[2] Jiang Y, Ma D, Wright K, Seiberlich N, Gulani V, Griswold MA. Simultaneous T1, T2, diffusion and proton density quantification with MR fingerprinting. Magn. Reson. Imaging. 2013;38(1):173-9.
[3] Weigel M, Schwenk S, Kiselev VG, Scheffler K, Hennig J. Extended phase graphs with anisotropic diffusion. Journal of magnetic resonance. 2010 Aug 31;205(2):276-85.
[4] Torrey HC. Bloch equations with diffusion terms. Physical review. 1956 Nov 1;104(3):563.
[5] Seroussi I, Grebenkov DS, Pasternak O, Sochen N. Microscopic interpretation and generalization of the Bloch-Torrey equation for diffusion magnetic resonance. Journal of Magnetic Resonance. 2017 Apr 30;277:95-103.
[6] Ben‐Eliezer N, Sodickson DK, Block KT. Rapid and accurate T2 mapping from multi–spin‐echo data using Bloch‐simulation‐based reconstruction. Magnetic resonance in medicine. 2015 Feb 1;73(2):809-17.
[7] Oakden W, Stanisz GJ. Effects of diffusion on high‐resolution quantitative T2 MRI. NMR in Biomedicine. 2014 Jun 1;27(6):672-80.
[8] Xu J, Does MD, Gore JC. Numerical study of water diffusion in biological tissues using an improved finite difference method. Physics in medicine and biology. 2007 Mar 12;52(7):N111.
Figures