4263
Multiband Multi-slab Magnetic Resonance Fingerprinting Using Overlapping Slabs and Temporal-Sharing Reconstruction1Department of Diagnostic Radiology, The University of Hong Kong, Hong Kong, Hong Kong, 2Philips Healthcare, Hong Kong, Hong Kong
Synopsis
Magnetic Resonance Fingerprinting (MRF) is a novel and rapid technique to quantify multiple MR parameters, and single-slab MRF was later developed for better slice coverage. In this study, we proposed a new method to extend single-slab MRF to multiband multi-slab acquisition. The slab boundary artifacts due to imperfect slab profile in multi-slab acquisition is overcome by a overlapping-slab acquisition strategy, and MRF reconstruction from the multiband multi-slab data can be obtained using our previously proposed temporal sharing reconstruction method.
Purpose
Magnetic resonance fingerprinting (MRF) 1 , a novel and rapid approach to quantify multiple MR parameters, has been extended to single-slab acquisition for better slice coverage and through-plan resolution. To further improve the acquisition efficiency of single-slab MRF, a multi-slab approach to 3D MRF 2 is warranted. There are however two major challenges in multi-slab MRF, namely (1) the presence of slab boundary artifacts due to imperfect slab profile, and (2) conventional multi-slab acquisition strategy is not optimal due to insufficient time within the short TR in MRF acquisition. We therefore propose a multiband multi-slab MRF approach, wherein overlapping slabs acquisition strategy is developed to overcome slab boundary artifacts, and multiband multi-slab acquisition is used to enable acceleration along the slab direction, the data of which are then reconstructed by the temporal-sharing MRF reconstruction method that we previously proposed 3 to reduce the g-factor penalty.Methods
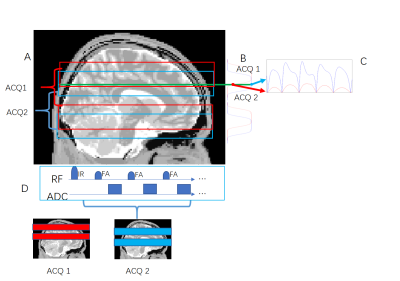
Multiband multi-slab MRF: Slices at slab boundaries suffer from signal loss due to imperfect slab profile in multi-slab acquisition, compromising the fidelity of MRF dictionary matching. As shown in Figure 1, with overlapping slabs acquisition, the slice with boundary artifacts in one slab (red slab) is acquired again in the next slab acquisition (blue slab) where the slab profile overlaps with the previous one, thereby correcting erroneous signal evolution. Notice that in each slab acquisition, multiple slabs are excited simultaneously to increase acquisition efficiency, and that phase modulation that is analogous to that of tblip-MRF is applied to the slabs for different dynamics.
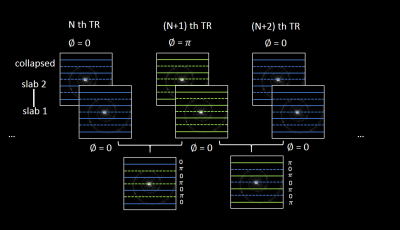
Temporal sharing reconstruction: Temporal sharing (tsSMS) is used to separate the coupled but phase-modulated slabs from the multiband acquisition strategy as mentioned above. Slab-aliased stack of spiral k-space data were first regridded into Cartesian k-space using nuFFT. Composite k-space (bottom row of Figure 2) at a given dynamic is then obtained by slicing and sharing the k-space of consecutive dynamics, resulting in phase modulation along the phase-encoding direction that is consistent with CAIPIRHINHA 4 shift. Figure 2 illustrates the reconstruction algorithm for the case of multiband factor (MB) = 2. The composite k-space signal after temporal sharing at a given TR can be defined as:$$ S_{z,t',j}^{ts} = \sum_{\tau = 1}^{MB} {\delta_{mod(j,N),mod(\tau,N)} \phi_{z,t'+\tau -1}^{t-Blipped} S_{z,t`+\tau-1,j}} $$
where $$$ S_{z,t',j}^{ts} $$$ is k-space data of zth slice, t’th TR and jth ky lines. $$$ \phi_{z,t}^{t-Blipped} = e^{i2\pi(z-1)(t-1)/MB} $$$. And images reconstructed from this k-space is:$$ \hat{\rho}_{z,t'}(y) = \sum_{\tau = 1}^{MB} \left\{\rho_{z,t'+\tau-1}(y-(1-z)\frac{FOV}{MB})+\sum_{|q|\leq{MB-1},\neq0}\rho_{z,t'+\tau-1}(y-(q+1-z)\frac{FOV}{MB})e^{iq2\pi(\tau-1)/MB}\right\}\phi_{z,t'}^{t-Blipped}/MB $$
where $$$ \rho_t = F_j^{-1}\left\{\phi_t^{t-Blipped}S_t\right\} $$$. The terms in the second summation are considered negligible with the assumption $$$ \rho_t'\approx...\approx\rho_t'+MB-1 $$$, considering the signal changes within a short window are relatively consistent.
Experiments: All data were simulated using a numerical brain obtained from https://github.com/leoliuf/MRiLab, and signals are simulated using a IR-FISP sequence with 1000 dynamics. Stack of variable-density spiral acquisition was simulated in each slab with 48x undersampling and 5.8 ms acquisition window for each TR. Spiral waveforms is rotated by a golden angle (222.5 degree) in each TR. Other imaging parameters in the simulation include: in-plane FOV = 300 mm, flip angle = 0 ~ 60 degree, TR = 14~16 ms. Multiband multi-slab MRF data were simulated from single-slab MRF datasets with slab and time dependent phase modulation that is analogous to that of tblip-MRF 5.
Results
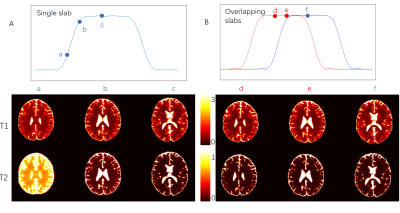
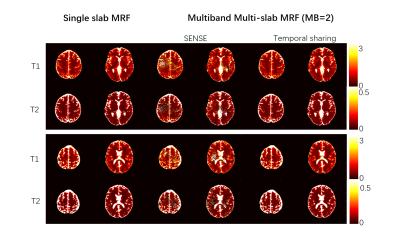
Figure 3 shows the results obtained from single-slab MRF and multi-overlapping-slab MRF. The fidelity of dictionary matching at the slab boundaries is severely compromised due to imperfect slab profile with single-slab acquisition, whilst that with multi-overlapping-slab is not. Figure 4 shows the single-slab MRF results, and multiband multi-slab MRF results with slice-SENSE reconstruction and with our proposed temporal sharing reconstruction for MB = 2. The improvement in the fidelity of dictionary matching is apparent with the use of our proposed temporal sharing.Discussion
We have successfully demonstrated that single-slab MRF can extended to multi-slab acquisition using overlapping slabs and multiband acquisition with temporal sharing reconstruction. We overcame the slab boundary artifacts due to imperfect slab profile in multi-slab acquisition by using overlapping-slab acquisition. With our multiband multi-slab MRF, additional freedom in acceleration can be achieved in the through-slab direction. On the other hand, we have utilized temporal sharing for the reconstruction of multiband data. Due to the signal consistency in adjacent TR, CAIPIRINHA-shift amongst the slabs can be achieved by slicing and sharing the adjacent k-space, noting that spiral data are regridded into Cartesian data, leading to reduction in G-factor penalty. As a comparison, slice-SENSE cannot effectively separate slabs, likely because of the presence of additional artifacts due to in-plane undersampling, whilst temporal sharing is less susceptible. In conclusion, multiband multi-slab MRF can be successfully achieved with our proposed overlapping-slab acquisition and temporal sharing reconstruction.Acknowledgements
No acknowledgement found.References
1. Ma, Dan, et al. "Magnetic resonance fingerprinting." Nature495.7440 (2013): 187-192.
2. Ma, D., Jiang, Y., Chen, Y., McGivney, D., Mehta, B., Gulani, V., & Griswold, M. (2017). Fast 3D magnetic resonance fingerprinting for a whole‐brain coverage. Magnetic Resonance in Medicine.
3. Cui, D., et al. "Simultaneous multi-slice MRF with controlled aliasing enabled by temporal data sharing." Annual Meeting and Exhibition of the International Society for Magnetic Resonance in Medicine, ISMRM 2016. 2016.
4. Breuer, F. A., Blaimer, M., Heidemann, R. M., Mueller, M. F., Griswold, M. A., & Jakob, P. M. (2005). Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi‐slice imaging. Magnetic resonance in medicine, 53(3), 684-691.
5.
Ye,
H., Ma, D., Jiang, Y., Cauley, S. F., Du, Y., Wald, L. L., ... &
Setsompop, K. (2016). Accelerating magnetic resonance fingerprinting
(MRF) using t‐blipped simultaneous multislice (SMS)
acquisition. Magnetic
resonance in medicine, 75(5),
2078-2085.
Figures