4261

MORE-MRF: Towards Motion Resolved Cardiac Multi-Parametric Mapping with Magnetic Resonance Fingerprinting
Olivier Jaubert1, Gastao Cruz1, Torben Schneider2, Rene Botnar1, Daniel Rueckert3, and Claudia Prieto1

1Biomedical Engineering, King's College London, London, United Kingdom, 2Philips Healthcare, London, United Kingdom, 3Department of Computing, Imperial College, London, United Kingdom

Synopsis

Magnetic Resonance Fingerprinting (MRF) estimates multi-parametric maps simultaneously with short acquisition times. Cardiac MRF has been recently proposed to quantify myocardial T1 and T2 maps for 2D single-phase cardiac imaging. This ECG-triggered breath–hold approach provides a single-phase cardiac image and uses a non-continuous (segmented) acquisition. Here we sought to investigate myocardial MRF at multiple cardiac phases from a continuous acquisition, which could simultaneously provide cardiac function and quantitative tissue characterisation. The proposed approach was evaluated in simulations and healthy subjects, considering eight cardiac phases per cycle.

Introduction

Magnetic Resonance Fingerprinting1 (MRF) has shown promise to map parameters faster than conventional methods via simultaneous multi-parametric mapping. MRF has been recently proposed to rapidly quantify simultaneously T1 and T2 in the myocardium for 2D single-phase cardiac imaging2. This approach uses an ECG-triggered acquisition with variable magnetization preparation pulses. One limitation of this method2 is the inherent data inefficiency of the triggered acquisition. Here we propose a “free-running” continuous acquisition to enable myocardial MRF at multiple cardiac phases (MORE-MRF), which could simultaneously provide cardiac function and quantitative tissue characterisation. The proposed approach was evaluated in simulations and in-vivo in four healthy subjects,considering eight cardiac phases.

Methods

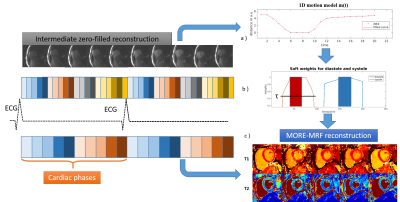
Acquisition. A pseudo-balanced SSFP3 (pSSFP) golden radial acquisition with inversion recovery (IR) pulses applied throughout the acquisition, to ensure sufficient encoding for multiple cardiac phases, was developed. The flip angle (FA) pattern was similar to the one in4 and was repeated during the scan. TR was computed as to preserve the pSSFP conditions (Fig.1), while TE was fixed for simplicity. ECG signal was used to retrospectively bin the data into to different cardiac phases (Fig.2).

Reconstruction: Parallel imaging, low rank inversion5, soft-weighting6 and locally low rank regularisation7 were combined to reconstruct multiple phases of the cardiac cycle. This was achieved by solving:

$$\hat{\textit{I}_c}=\underset{I_c}{\mathrm{argmin}}\Vert W_c(\textbf{E} \textbf{U}_{Rc}\textit{I}_c-\textbf{K}_c)\Vert_2^2+\lambda\sum_{b}\Vert\textbf{R}_{b}\textit{I}_c\Vert_*$$

where $$$\hat{\textit{I}_c}$$$ is the compressed time-point image series at cardiac phase c, E is the SENSE encoding operator, Kc is the acquired k-space data at phase c, URc is the low rank operator obtained truncating (to the appropriate rank R) a singular value decomposition of the soft-weighted MRF dictionary at phase c, $$$\textbf{R}_{b}$$$ thresholds the singular value decomposition of an image block b and $$$\lambda$$$ controls the regularization strength. The soft-weights for cardiac phase c, $$$W_c$$$ is defined for every time-point acquired at time t by:

$$W_c(t)=\begin{cases}1\quad,\quad if\quad |t-t_c|<\frac{S_c}2\\e^{-\alpha(m(t)-m(t_c)) }\quad,\quad if\quad e^{-\alpha(m(t)-m(t_c))}>\tau\quad and\quad |t-t_c|>\frac{S_c}2\\0 \quad, \quad otherwise\end{cases}$$

where $$$\alpha$$$ is a scaling factor, $$$\tau$$$ a threshold value to discard low weighted time-points,$$$S_c$$$ the size of phase c,$$$m(t)$$$ the cardiac motion model and $$$t_c$$$ the center of phase c. An estimation of the cardiac motion $$$m(t)$$$ is obtained from the data itself by an intermediate zero-filled CINE reconstruction (Fig.2), enabling identification of the quiescent and motion intensive periods of the cardiac cycle. A dot product matching between the reconstructed data and the soft-weighted dictionary8 was applied to obtain the T1 and T2 maps.

Experiments: A digital static cardiac phantom (MRXCAT9) was simulated using realistic T1 and T2 values for myocardium, blood and liver, and a model $$$m(t)$$$ for a heart-rate of 53 beats/minute. Motion was not considered in the simulations to isolate the effects of the encoding and the proposed reconstruction. IR pulses and FA pattern were repeated every 2.92s, considering a 29.5 sec scan. Four healthy subjects were scanned in a 1.5T Philips MR scanner using anterior and posterior coils (28-channels). Acquisition parameters included: TE=2ms, 4380 time-points, one spoke per time-point, 2x2 mm2 resolution, 300x300 mm2 FOV and 10 mm slice thickness, 6 repetitions of IR and flip angle train, acquisition time=17.7s compatible with a breath-hold. $$$\alpha$$$ and $$$\tau$$$ were set empirically for both simulations and in-vivo reconstructions. For both cases, eight cardiac phases were retrospectively reconstructed, with R=8, b=7 and local rank threshold=5% of the maximum singular value.


Results

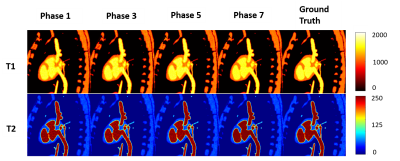
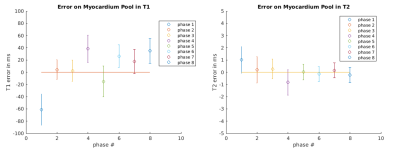
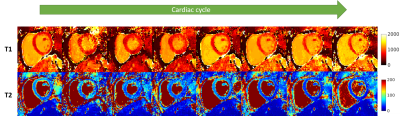
T1 and T2 parametric maps obtained from simulations are shown in Fig.3. The mean error on a region of interest throughout the cycle was measured as 5.9±32.5ms and 0.05±0.5ms for T1 and T2, respectively (Fig.4). Fig.5 shows the resulting T1 and T2 maps for eight cardiac phases in a healthy subject. In-vivo mean values throughout the cycle were measured as 922±65ms and 42±7.9ms for T1 and T2, respectively. Natural variation of T1 between cardiac phases (reported at ~22ms between systole and diastole10) and sources of bias such as B0 and B1 inhomogeneity, flow, persistent motion, variable parametric encoding per cardiac phase, presence of fat and the reduced amount of data could explain a higher inter phase variability in the in-vivo results compared to the simulations.

Conclusions

A continuous free-running myocardial MRF acquisition has been proposed which could enable simultaneous cardiac function and quantitative tissue characterisation. Initial proof of concept evaluations in simulations and healthy subjects show the feasibility of the proposed method. Some bias in T1 and T2 myocardial values along the different cardiac phases was observed in-vivo. Future work will aim to reduce bias and standard deviation and compare our method to conventional T1 and T2 mapping methods.

Acknowledgements

This work was supported by:

-Philips Healthcare,

-EPSRC programme Grant (EP/P001009/1),

-FONDECYT 1161055,

-King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1).


References

1.Ma D et al, Nature 2013;495:187-192

2. Hamilton et al, MRM 2017;77: 1446–1458.

3. Asslander et al, MRM, 2017;77(3):1151–1161

4. Asslander et al, arXiv, 2017;1703.00481

5. McGivney et al, IEEE Trans Med Imaging 2014;33(12):2311-22

6. Johnson et al, MRM, 2012;67:1600-1608

7. Cao et al, MRM, 2017;78:1579–1588

8. Cruz et al, ISMRM 2018, submitted

9. Wissmann L et al,JCMR 2014;16:63.

10. Reiter et al, Radiology 2014;271:365–372.

Figures

Figure 1. One repetition of the flip angle train and repetition time train containing 730 values for an acquisition time of 2.92s per repetition. Each repetition of the pattern is preceded by an IR and the TE is fixed at 2ms.

Figure 2. Proposed MORE-MRF framework. a) A 1D cardiac motion model m(t) is estimated from an intermediate retrospectively ECG-gated zero-filled reconstruction. ECG signal is also used to retrospectively assign the time-points to different cardiac phases. b) Weights for the proposed reconstruction are obtained from the estimated cardiac motion model (Eq.2). Soft-weights (lines) are compared to a hard-weight (bars) approach. c) MORE-MRF reconstruction is performed combining soft-weights and regularized low rank reconstruction of T1 and T2 maps for each cardiac phase.

Figure 3. T1 (first row) and T2 (second row) maps from cardiac phases 1, 3, 5 and 7 from simulated data reconstructed with MORE-MRF. Good quality T1 and T2 maps are obtained for all cardiac phases. T1 and T2 maps are visually consistent with ground truth maps (last column) throughout the different cardiac phases. Cardiac motion was not considered in the simulations to isolate the effects of the proposed encoding and the soft-weighted reconstruction.

Figure 4. T1 and T2 errors in comparison to ground truth values for all cardiac phases with the proposed approach. Values were measured on a region of interest of the simulated myocardium. Bias under 6 % were obtained for all cardiac phases for both T1 and T2 values. Error on all phases was measured at 5.9±32.5ms and 0.05±0.50ms for T1 and T2 respectively. A higher bias is observed in T1 for the first phase, which coincides with the acquisition of the first inversion pulse.

Figure 5 . In-vivo MORE-MRF. T1 and T2 maps for eight cardiac phases in a healthy subject. Septal myocardium values were measured as 922±65ms and 42±7.9ms throughout the cycle for T1 and T2 respectively. Functional cardiac contraction and relaxation can be observed throughout the cardiac cycle. Blood behaviour was not modelled, therefore values are expected to differ from phase to phase.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4261