4257

MRF-FrM: A Preliminary Study on Improving Magnetic Resonance Fingerprinting Using Fractional-order Models

Haifeng Wang¹, Leslie Ying², Xin Liu¹, Hairong Zheng¹, and Dong Liang¹

¹Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, ²Department of Biomedical Engineering and Department of Electrical Engineering, The State University of New York, Buffalo, NY, United States

Synopsis

Magnetic resonance fingerprinting (MRF) is an exceptional promise for simultaneous quantification of T1 and T2 maps, based on the traditional Bloch equation formalism of MR and numerous readouts. In this work, a Fractional-order model of the Bloch equations is applied to create the dictionary of the T1 and T2 maps used in MRF. The simulations show that the proposed method can improve the evaluation accuracy of the T1 and T2 maps comparing with the conventional MRF methods with the traditional first-order model of the Bloch simulation.

Introduction

Recently, magnetic resonance fingerprinting (MRF) shows an exceptional promise for simultaneous quantification of T1 and T2 maps, based on the traditional Bloch equation formalism and numerous readouts ¹. Though the performance of the MRF acquisitions are similar to modern rapid combined T1 and T2 mapping methods DESPOT1 and DESPOT2 ², the evaluation accuracy of the T1 and T2 maps is still a problem in MRF ^1,3-7. Since now, many schemes have been proposed to improve the accuracy of the MRF from matching, reconstructions and sequences ^3-15, such as SVD compression ³, maximum likelihood ⁴, Low-Rank (LR) ^5-9, B1 estimation ¹⁰, pseudo steady-state free precession (pSSFP) ¹¹, sliding-window ¹², slice profile compensation ¹³, multi-frequency interpolation ¹⁴, Kalman filter ¹⁵, etc. But they are all based on the first order model of the conventional Bloch equations. It has been demonstrated that the fractional-order model of the Bloch equations can describe anomalous NMR or MRI relaxation phenomena (T1 and T2) ¹⁶ more accurately. In this work, the fractional-order extension of the Bloch equations is applied to improve the dictionary accuracy for the T1 and T2 map evaluations. The simulations illustrate that the proposed method can raise the accuracy of the T1 and T2 maps higher over 30% than the conventional MRF with the first-order model of the Bloch equations.

Theory and Methods

It is well-known that the Bloch equations are wildly used to describe the dynamics of motion of macroscopic nuclear magnetization that can be obtained by summing up all nuclear magnetic moment in the sample. But, there are many anomalous cases are observed such as stretched-exponential or power-law behaviour. So it is necessary to look for an alternative model to describe the mathematical relationship between relaxation processes and internal material structure. As seen as Fig.1, a fractional-order model for NMR or MRI relaxation has been proposed by R.L. Magin et. al ¹⁶, which leads to Mittag-Leffler and stretched exponential functions for time-domain T1 and T2 relaxation. Actually, the fractional-order model has shown by others to be useful for describing dielectric and viscoelastic relaxation in complex, heterogeneous materials ¹⁶. To revert to the equivalent differential form for generating the dictionary in MRF, we applied the fractional derivatives of order α (0<α≤1) and β (0<β≤1) to T2 and T1 relaxations respectively, and obtained the following form for the fractional-order components of the Bloch equations in Fig.1. When α and β are both equal to 1, the Mittag-Leffler function is equivalent to the simple exponential function and the classical expression for T1 and T2 relaxation emerges. And with small values of the function argument, the Mittag-Leffler function converges to the stretched exponential function with the stretching parameters (α and β), as seen in Fig. 1. Therefore, the conventional Bloch equations in MRF are substituted by the Bloch equations with the fractional-order model. Here, the acquisition pattern with 850 shots of variant flip angles (FA), time of repetition (TR) and time of echo (TE) was used by pSSFP and a golden-angle radial trajectory with the degree: 111.25° increment is employed in k-space ¹¹, as seen in Fig. 2. A Shepp-Logan phantom with 5 materials is applied in all of the simulations. The two reconstruction methods of SVD back projection ³ and LR ADMM reconstruction ⁵ were used to solve the MRF reconstruction problem to estimate T1 and T2 maps.

Results

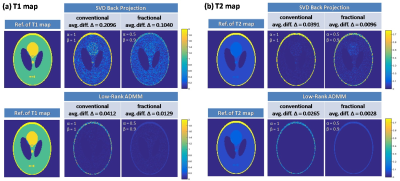
Fig. 3 shows the estimated T1 (a) and T2 (b) maps of MRF with conventional Bloch equations and the proposed fractional Bloch equations. Here, α and β (0<α≤1, 0<β≤1) in the proposed equations are respectively equal to 0.5 and 0.9. The average difference (avg. diff. Δ) maps between the reference maps and estimated T1 or T2 maps illustrate that the proposed method can reduce over 30% the evaluation errors of the T1 and T2 map, when α and β of the fractional-order model have appropriate values.

Discussion and Conclusion

In sum, we applied the fractional-order model into the Bloch equations in MRF, in order to improve the evaluation accuracy of the T1 and T2 maps. The simulation results have shown the potential of raising the evaluation accuracy in two types of MRF reconstruction methods. In the future, in vivo experiments and automatically setting stretching parameters (α and β) will be studied.

Acknowledgements

The authors thank Dr. Huihui Ye and Chongyu Liao for helpful discussions, and thank Dr. Jakob Asslaender for his open-source codes. This work was supported in part by the National Natural Science Foundation of China (61471350) and the Science and Technology Program of Guangdong (2015A020214019).

References

1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013; 495(7440):187-92.

2. Deoni SCL, Peters TM, Rutt BK. High-Resolution T1 and T2 Mapping of the Brain in a Clinically Acceptable Time with DESPOT1 and DESPOT2. Magnetic Resonance in Medicine. 2005; 53:237-41.

3. McGivney DF, Pierre E, Ma D, Jiang Y, Saybasili H, Gulani V, Griswold MA.SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans Med Imaging. 2014 Dec;33(12):2311-22.

4. Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting. IEEE Trans Med Imaging. 2016 Aug;35(8):1812-23.

5. Asslaender J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med. 2017 Mar 5. doi: 10.1002/mrm.26639.

6. Zhao B, Setsompop K, Adalsteinsson E, Gagoski B, Ye H, Ma D, Jiang Y, Ellen Grant P, Griswold MA, Wald LL. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn Reson Med. 2017 Apr 15. doi: 10.1002/mrm.26701.

7. Yang M, Ma D, Jiang Y, Hamilton J, Seiberlich N, Griswold MA, McGivney D. Low rank approximation methods for MR fingerprinting with large scale dictionaries. Magn Reson Med. 2017 Aug 13. doi: 10.1002/mrm.26867.

8. Doneva M, Amthor T, Koken P, Sommer K, Bornert P. Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data. Magn Reson Imaging. 2017 Sep;41:41-52.

9. Mazor G, Weizman L, Tal A, Eldar YC. Low rank magnetic resonance fingerprinting. Conf Proc IEEE Eng Med Biol Soc. 2016 Aug;2016:439-442.

10. Buonincontri G, Sawiak SJ. MR fingerprinting with simultaneous B1 estimation. Magn Reson Med. 2016 Oct;76(4):1127-35.

11. Asslander J, Glaser SJ, Hennig J. Pseudo Steady-State Free Precession for MR-Fingerprinting. Magn Reson Med. 2017 Mar;77(3):1151-1161.

12. Cao X, Liao C, Wang Z, Chen Y, Ye H, He H, Zhong J. Robust sliding-window reconstruction for Accelerating the acquisition of MR fingerprinting. Magn Reson Med. 2017 Oct;78(4):1579-1588.

13. Hong T, Han D, Kim MO, Kim DH. RF slice profile effects in magnetic resonance fingerprinting. Magn Reson Imaging. 2017 Sep;41:73-79.

14. Ostenson J, Robison RK, Zwart NR, Welch EB. Multi-frequency interpolation in spiral magnetic resonance fingerprinting for correction of off-resonance blurring. Magn Reson Imaging. 2017 Sep;41:63-72.

15. Zhang X, Zhou Z, Chen S, Chen S, Li R, Hu X. MR fingerprinting reconstruction with Kalman filter. Magn Reson Imaging. 2017 Sep;41:53-62.

16. Magin RL, Li W, Pilar Velasco M, Trujillo J, Reiter DA, Morgenstern A, Spencer RG. Anomalous NMR relaxation in cartilage matrix components and native cartilage: fractional-order models. J Magn Reson. 2011 Jun; 210(2):184-91.

Figures

Fig 1. The Fractional-order model of the proposed Bloch equations. If small values of function argument, we assume that the Mittag-Leffler function is approximately equal to the stretched exponential function with the stretching parameter.

Fig 2. The MRF sequence pattern. (a) is the acquisition sequence diagram; (b) presents a radial trajectory with a golden angle (Degree: 111.25°) increment; (c) shows variant flip angles; (d) TR and TE pattern of the pSSFP MRF sequence ¹¹.

Fig 3. The average difference (avg. diff. Δ) maps between the reference maps and the estimated T1 (a) and T2 (b) maps, respectively acquired from the conventional Bloch equations and the proposed fractional Bloch equations. The SVD back projection ³ and LR ADMM reconstruction ⁵ are applied to solve the MRF reconstruction problem. In the conventional, α and β in the proposed equations are respectively equal to 1.0 and 1.0. In the fractional, α and β in the proposed equations are respectively equal to 0.5 and 0.9.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

4257