4252

Diffusion Propagator Formalism in Bloch Equation Simulation of Magnetic Resonance Fingerprinting
Shota Hodono1, Yun Jiang2, Naren Nallapareddy3, Vikas Gulani2, and Mark Griswold2

1Physics and Astronomy, Ohio Northern University, Ada, OH, United States, 2Radiology, Case Western Reserve University, Cleveland, OH, United States, 3Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States

Synopsis

By considering spin diffusion as a random walk process and introducing a Gaussian probability function to the Bloch equation, a diffusion propagator was developed, which allows diffusion to be accounted for in magnetic resonance fingerprinting (MRF) simulations. In this study, signal intensities generated by Bloch simulations with the diffusion propagator were compared with theoretical values for the diffusion-weighted spin echo sequence. Additionally, the diffusion propagator approach was applied to the MRF fast imaging with steady-state precession sequence and the resulting signal evolution was qualitatively compared with that generated by the Extended Phase Graphs method.

Introduction

Magnetic resonance fingerprinting1 (MRF) can provide efficient method to quantify multiple characteristic tissue properties by matching the acquired signal to a pre-calculated dictionary containing all possible signal evolutions. While early MRF work has shown some promising results for quantification of T1 and T2, MRF also has the potential to derive other physiological tissue properties, such as diffusion and perfusion. The purpose of this work was to implement and evaluate a diffusion propagator in MRF Bloch simulations in order to generate dictionaries which include diffusion coefficients, and assess its application to a representative MRF acquisition. The established diffusion propagator approach was evaluated for a conventional diffusion-weighted spin echo sequence by comparing the signal intensities with theoretical values, and was subsequently applied to the MRF-Fast Imaging with Steady-state Precession (FISP) sequence2.

Theory

By considering a random walk process and introducing a Gaussian probability function to the Bloch equations, a magnetization change under random diffusion of spin in a constant magnetic field gradient can be expressed using a diffusion propagator approach as follows3-5:

$$$m^+(x_l)=\sum_{q=l-l_{6\sigma}}^{l+l_{6\sigma}}\left\{P_r(x_l-x_q)E_{TD}m^-(x_q)\right\}+E_L$$$ [1]

where $$$m^+$$$ and $$$m^-$$$ are the final and initial magnetization, respectively, $$$P_r(x_q-x_l)=\frac{TH}{N\sqrt{4\pi D\Delta t}}exp(-\frac{(x_l-x_q)^2}{4D\Delta t})$$$, $$$E_{TD}=\begin{bmatrix}E_DE_2\cos(\frac{\phi_l+\phi_q}{2})&-E_DE_2\sin(\frac{\phi_l+\phi_q}{2})&0\\E_DE_2\sin(\frac{\phi_l+\phi_q}{2})&E_DE_2\cos(\frac{\phi_l+\phi_q}{2})&0\\0&0&E_1\end{bmatrix}$$$, $$$E_L=\begin{bmatrix}0\\0\\1-E_1\end{bmatrix}$$$, $$$E_D=exp(-\frac{\gamma^2G^2(\Delta t)^3D}{12})$$$, $$$E_1=exp(-\frac{\Delta t}{T_1})$$$, $$$E_2=exp(-\frac{\Delta t}{T_2})$$$, $$$\sigma=\sqrt{2D\Delta t}$$$, and $$$\gamma$$$ is the gyromagnetic ratio.

In this work, we defined $$$N$$$spins equally distributed across the slice thickness, $$$TH$$$. To simplify the discussion, we considered that the applied gradient produces a total of $$$2\pi n$$$ dephasing across the slice thickness (where $$$n$$$ is an integer) during $$$\Delta t$$$ seconds. Thus, the $$$l$$$th spin, positioned at $$$x_l$$$ ($$$l=1,2,...,N,x_N=TH$$$), acquires a phase due to the gradient, $$$\phi_l=\frac{2\pi n}{N}l $$$. Fig.1 provides a visual aid for understanding eq. [1] and the associated summation limits. When the magnetic field gradient is turned off, eq. [1] reduces to:

$$$m^+(x_l)=\sum_{q=l-l_{6\sigma}}^{l+l_{6\sigma}}\left\{P_r(x_l-x_q)E_{T}m^-(x_q)\right\}+E_L$$$ [2]

where $$$E_T=\begin{bmatrix}E_2&0&0\\0&E_2&0\\0&0&E_1\end{bmatrix}$$$.

Methods

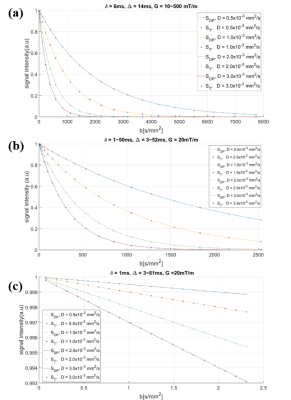
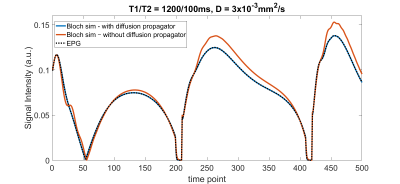
Bloch simulations with the diffusion propagator expressed by eq. [1] and [2] were performed for the diffusion weighted spin echo sequence (Fig.2). Resulting signal intensities, $$$S_{DP}$$$, were compared with theoretical values calculated from the sequence parameters, assuming a mono-exponential decay model of diffusion: $$$S_T=S_0exp(-bD)$$$, where $$$b=\gamma^2G^2\delta^2(\Delta-\frac{\delta}{3})$$$. In order to focus specifically on the diffusion decay, T1 and T2 values were set to $$$\infty$$$ in this study, hence $$$S_0=1$$$. Parameters of the sequence and $$$D$$$ values were varied according to conventional MRF acquisitions and typical values in tissues, respectively (Fig.2). The diffusion propagator approach was evaluated using three separate conditions: (a) fixing $$$\delta$$$ and $$$\Delta$$$, varying the magnitude of $$$G$$$, (b) varying $$$\delta$$$ with fixed $$$G$$$, (c) varying $$$\Delta$$$ with fixed $$$\delta$$$ and $$$G$$$. Percentage errors between $$$S_{DP}$$$ and $$$S_T$$$ were calculated for each signal intensity value: $$$Error=\frac{|S_T-S_{DP}|}{S_T}\times$$$100[%].The diffusion propagator approach was also applied to the MRF-FISP sequence. The signal evolution was qualitatively compared to that generated by the Extended Phase Graphs6 (EPG) method, an established fast and robust means to simulate MRI signal behavior with diffusion coefficients.

Results and Discussion

Each simulated signal intensity $$$S_{DP}$$$ was found to closely match the intensity predicted by conventional diffusion MRI theory, $$$S_T$$$ (Fig.3). This approach was robust to changes in the spin echo sequence parameters ($$$G, \delta$$$ and $$$\Delta$$$): in all cases, calculated errors were low, are shown in Fig.4. For conditions (a) and (b), magnetization decay was governed by magnetic field gradients (eq. [1]), whilst for condition (c), $$$\delta$$$ was fixed to 1ms and $$$\Delta$$$ was varied to specifically observe the effect of free diffusion on the signal decay, as described by eq. [2]. The diffusion propagator based Bloch simulations showed robustness to all three conditions and good agreement with the theoretical diffusion-induced signal decay for the diffusion-weighted spin echo sequence. As Fig.5 shows, the MRF-FISP signal evolution generated from the Bloch equations with diffusion propagator closely matched that generated by EPG, whilst considerable discrepancies were observed when running Bloch simulations without the diffusion propagator. This diffusion propagator approach should permit MRF dictionary to include both of diffusion coefficients and off-resonance frequencies which is not taken into account of by EPG. The diffusion propagator approach is fully compatible with arbitrary relaxation behavior and therefore should enable accurate mapping of T1, T2 and diffusion coefficients with MRF, in addition to supplementing existing MRF dictionaries with diffusion coefficient information, in the near future.

Conclusion

We have introduced a diffusion propagator approach in Bloch equation simulations and demonstrated its robustness when applied to the diffusion-weighted spin echo sequence and MRF-FISP sequence by showing good agreement with conventional diffusion MRI theory. The generality of this formalism should permit the inclusion of quantitative diffusion coefficients in MRF dictionaries and improve the quality of MRF signal matching.

Acknowledgements

This work was supported by Siemens Healthcare and NIH grants 1R01EB016728, 1R01DK098503 and 1R01BB017219.

References

1. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192.

2. Jiang Y, et al. MR Fingerprinting Using Fast Imaging with Steady State Precession (FISP) with Spiral Readout, Magn. Reson. Med. 2015;74(6):1621-1631.

3. H. Y. Carr and E. M. Purcell. Effect of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954;94:630-636.

4. Gudbjartsson H, Patz S. NMR diffusion simulation based on conditional random walk. IEEE Trans Med Imaging 1995;14(4):636–642.

5. Yarnykh VL. Optimal Radiofrequency and Gradient Spoiling for Improved Accuracy of T1 and B1 Measurements Using Fast Steady-State Techniques. Magn Reson Med. 2010;63(6):1610-1626.

6. Weigel. M. Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple. J Magn Reson Imaging. 2015;41(2):266-295.

Figures

Figure 1. Visual aid for interpretation of eq. [1]. When running Bloch simulations using the diffusion propagator for MRF, the width of the Gaussian probability function, $$$\sigma$$$, and the distance between each spin, $$$\frac{TH}{N}$$$, should be carefully chosen to maintain accuracy of the summation in eq. [1]. If the distance between spins is larger than the width of the Gaussian function, appropriate summation is not obtained.

Figure 2. Diffusion-weighted spin echo sequence parameters (a) and sequence diagram (b). The centers of the diffusion gradients were placed in the middle of the separation of the RF excitations and signal acquisition.

Figure 3. Results of comparison of and for conditions (a), (b), and (c) as described in the Methods section. Additional parameters were as follows: (a) $$$N$$$=500spins, $$$TH$$$=8$$$\times$$$10-5m, (b) and (c) $$$N$$$=2000spins, $$$TH$$$=5$$$\times$$$10-4m. As $$$\delta$$$ and $$$\Delta$$$ increase, the width of the Gaussian probability function becomes larger, therefore relatively larger number of spins and slice thickness were needed for conditions (b) and (c).

Figure 4. Percentage error between signal intensities derived from the diffusion propagator Bloch simulations, $$$S_{DP}$$$, and conventional diffusion theory, $$$S_T$$$. Quoted values represent the average ± standard deviation of errors for each condition and diffusion coefficient studied.

Figure 5. Signal evolution in the MRF-FISP sequence by Bloch simulations with diffusion propagator. The sequence diagram is described in another abstract (#4166, Hodono et al., submitted to ISMRM 2018). In this simulation, relatively large gradient amplitude, 56.3mT/m (24$$$\pi$$$ dephasing across the 5mm slice thickness during 1ms), was employed to accentuate signal decay due to diffusion.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4252