4246

Generation of Arbitrary Spectral Profiles using Orthonormal Basis Combinations of bSSFP MRI
Michael Mendoza1, Nicholas McKibben1, and Neal Bangerter1

1Electrical Engineering, Brigham Young University, Provo, UT, United States

Synopsis

We present a technique for generating an arbitrary spectral profile by using multiple-acquisition bSSFP. Multiple phase-cycled bSSFP images with increasing TRs were acquired and Gram-Schmidt orthogonalization was applied to spectral basis functions to generate an orthonormal basis. This generated orthonormal basis was used to approximate an arbitrary spectral profile by using linear combinations of the calculated basis functions. A variety of spectral functions were simulated and used as a template to approximate spectral profiles in water and fat phantoms.

Introduction

Balanced steady-state free precession (bSSFP) is a high SNR, fast imaging technique suffering from banding artifacts which degrade image quality. These banding artifacts are a function of off-resonance frequency and magnetic field inhomogeneities. Over the past two decades, several methods have been developed using multiple-acquisition bSSFP to either reduce the appearance of banding artifacts1,2,3 or to move the location of a banding artifacts to suppress undesired off-resonance frequencies4,5,6,7.

This work focuses on developing a novel technique for generating an arbitrary off-resonance spectral profile using multiple-acquisition bSSFP.

Theory

Using multiple phase-cycled bSSFP images with increasing $$$TR$$$, it is possible to form an orthonormal basis from which to approximate any arbitrary spectral profile. An orthonormal basis is a set of linearly independent vectors that can be used to span the complex numbers. A linear combination of basis vectors, $$$f_n$$$, can be used to approximate any analytical function $$$ f $$$ according to its basis expansion: $$$ f \simeq \hat{f} = \sum a_n f_n $$$. Increasing the number of terms in the basis expansion decreases the approximation error.

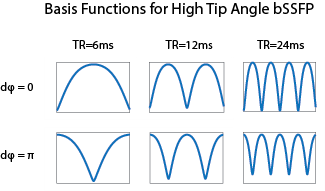
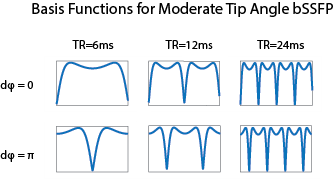
At large flip angles, bSSFP images have a sinusoidal-like shape spectral profile for certain tissues with a pass band region and region of signal null. Since the bSSFP profile is similar to sines and cosines, we can use multiple phase-cycled acquisitions to generate a basis similar to a Fourier series. The spectra used to generate this basis are shown in Figure 1. As this set of vectors is not exactly sinusoidal, it is not necessarily orthonormal. We therefore use Gram-Schmidt orthogonalization to generate an orthonormal basis. At moderate flip angles, the spectra generated appear less sinusoidal but can still form an acceptable approximating basis set (see Figure 2).

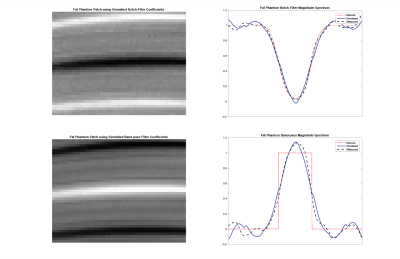
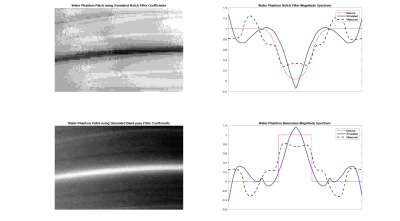
Multiple-echo acquisitions can be used to manipulate the spectral profile of a bSSFP image in order to create different contrast features and to suppress unwanted off-resonant frequencies (e.g., fat suppression). Using this technique we can approximate an arbitrary band-pass and notch filter as shown in Figures 3 and 4.

Methods

Six phase-cycled bSSFP images were acquired of a fat and water phantom using a high tip angle ($$$ 90^{\circ} $$$). These images were generated using two phase-cycled values ($$$ d \phi = 0^{\circ}, 180^{\circ} $$$) at three different $$$TR$$$ values, namely $$$TR = 6ms, 12ms, 24ms$$$, with $$$TE = TR / 2$$$. We then used Gram-Schmidt orthogonalization to generate an orthonormal basis. Using the desired spectral profile as a template function, the basis function coefficients were selected to approximate the desired bSSFP spectrum. These basis coefficients were computed by solving a linear system of equations, $$$ Ac=f $$$, with the basis forming the column space of $$$A$$$, $$$f$$$ the desired function, and $$$c$$$ the coefficients.

Results

After generating spectra for both the notch and band-pass filters, the resulting linear combinations shown in Figures 3 and 4 show successful filtering of the phantoms. In both the fat and water phantoms, the spectral profile was observed to be similar to those shown in Figures 1 and 2 respectively.

In fat, the notch filter was well approximated by the simulated and measured data, with side ripple levels below $$$10\%.$$$ The band-pass, with high frequency content, was approximated using a near sinusoidal basis, performing similarly to a Fourier series expansion. The resultant images show the spectrum profiles with strong induced signal peaks and nulls. The spectral approximations for the notch and band-pass filters in water were less accurate, with ripple levels in excess of $$$20\%.$$$ Although the measured data deviates from the simulated spectra, the general profile is observed in both filters and the signal peaks and nulls are pronounced in the resultant image.

Discussion

The method successfully generates off-resonance spectral profiles of both notch and band-pass filters in fat and water using multiple-acquisition bSSFP. Coefficients may be generated for arbitrary functions and may be more accurately approximated using additional terms. However, each term in the basis expansion corresponds to a new bSSFP acquisition at an increased $$$TR$$$ value. High resolution is required to resolve banding artifacts for high $$$TR$$$ values, leading to long acquisition times for desired spectrum profiles with high frequency content.

Fat suppression could be achieved with this technique by creating a notch filter spectrum and shifting the notch to the off-resonance frequency needed to suppress fat. This process requires the recalculation of basis coefficients such that the location of the null is steered to the desired location, similar to beam forming in phased-array antennas. In addition, accurate pixel-by-pixel reconstructions require a field map due to field inhomogeneities, further increasing acquisition time.

Acknowledgements

We would like to thank Bradley Bolster from Siemens for his support of the BYU MRI Research Facility

References

  1. Bangerter, et al. “Analysis of Multiple-Acquisition SSFP”, Magnetic Resonance in Medicine, 2004
  2. Vasanawala, et al. “Linear Combination Steady-State Free Precession MRI”, Magnetic Resonance in Medicine, 2000
  3. Xiang, Hoff. "Banding Artifact Removal for bSSFP Imaging with an Elliptical Signal Model, Magnetic Resonance in Medicine", 2014
  4. Vasanawala, et al. “Fluctuating Equilibrium MRI”, Magnetic Resonance in Medicine, 1999
  5. Hargreaves, et al. “Fat-suppressed steady-state free precession imaging using phase detection”, Magnetic Resonance in Medicine, 2003
  6. Leupold, et al. “Alternating repetition time balanced steady state free precession”, Magnetic Resonance in Medicine, 2006
  7. Quist, et al. “Simultaneous fat suppression and band reduction with large-angle multiple-acquisition balanced steady-state free precession”, Magnetic Resonance in Medicine, 2012

Figures

Figure 1: Magnitude plots of six basis functions generated from a high tip angle $$$(90^{\circ})$$$ SSFP simulation. The shape of this spectral profile was observed in images from the fat phantom. The top three basis functions are similar to the sine terms of the Fourier series, while the bottom three basis functions are similar to the cosine terms of the Fourier series.

Figure 2: Magnitude plots of six basis functions generated from a moderate tip angle SSFP simulation. The shape of this spectral profile was observed in images from the water phantom. The top three basis functions are odd functions, while the bottom three basis functions are even functions. Despite the unusual shape of this set of basis functions, it can be used to generate a variety of arbitrary off-resonance spectra after it has been orthogonalized with Gram-Schmidt orthogonalization.

Figure 3: Generated spectra from a fat phantom using the high flip angle basis functions. A shim gradient was applied from the top to the bottom of each image to create a range of off-resonance frequencies. The top row shows the spectral profile generated using a notch spectrum, the bottom row shows the spectral profile generated from a band-pass spectrum.

Figure 4: Generated spectra from a water phantom using the moderate flip angle basis functions. A shim gradient was applied from the top to the bottom of each image to create a range of off-resonance frequencies. The top row shows the spectral profile generated using a notch spectrum, the bottom row shows the spectral profile generated using a band-pass spectrum.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4246