Synopsis

The Gibbs artifact can be effectively eliminated by searching the local sub-voxel shifts (LSS) that minimize total variations, but it is only applicable to images reconstructed without zero padding. This work extends the LSS method to Gibbs artifact reduction in the presence of zero padding by introducing an interlaced total variation (iTV). The simulation and in vivo experimental results demonstrate that the proposed method can effectively remove Gibbs artifact in the presence of zero padding.

Purpose

Introduction

Gibbs artifact, also known as ringing artifact, in MR images is caused by the finitely acquired signal and mainly appears near high-contrast tissue boundaries. In clinic, Gibbs artifact may degrade diagnosis^2,3 and result in bias in following quantitative analysis^4-6. Recently, a local sub-voxel shifts (LSS) method was proposed to reduce Gibbs artifact by resampling the image at the zero crossings of the oscillating sinc-function¹. Although the LSS can efficiently eliminate the Gibbs artifact, it is not directly applicable to image reconstructed from the zero-padded k-space data, because zero padding varies the sampling pattern of the oscillating sinc-function. This work extends LSS to zero-padded k-space data by introducing interleaved total variation.

Methods

The signal is reconstructed for non-zero padded k-space data by:

$$f[n]=\sum_{\Omega=-\frac{N}{2}}^{\frac{N}{2} - 1}F[\Omega]e^{jn\frac{\Omega}{N}2\pi}$$

where the $$$F[\Omega]$$$ denotes the acquired non-zero padded k-space data, and the $$$f[n]$$$ denotes the reconstructed image.

However, in the zero-padded k-space case, taking m times zero-padded data for example, the image is reconstructed as follows:

$$f[n]_{m,padded}=\sum_{\Omega=-\frac{N}{2}m}^{\frac{N}{2}m - 1}F[\Omega]e^{jn\frac{\Omega}{mN}2\pi}$$

$$=\sum_{\Omega=-\frac{N}{2}}^{\frac{N}{2} - 1}F[\Omega]e^{jn\frac{\Omega}{mN}2\pi}$$

$$=\sum_{\Omega=-\frac{N}{2}}^{\frac{N}{2} - 1}F[\Omega]e^{j\frac{\Omega}{N}2\pi\frac{n}{m}}$$

Therefore, the $$$f[n]_{m,padded}$$$ can be considered as a m times denser sample of the non-zero padded reconstructed oscillation pattern $$$f[n]$$$.

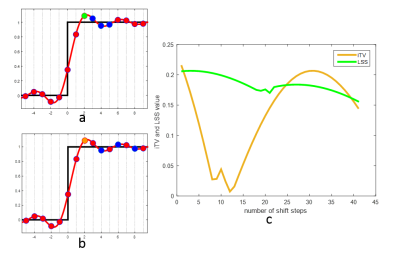
Based on the above description, we proposed a novel interlaced total variation (iTV) to extend LSS to zero padded case. For integer times zero padding, the iTV initially divides the denser samples into m individual oscillation patterns as shown in Figs. 1a and 1b, and then performs the LSS on each individual oscillation patterns. For non-integer times zero padding, we first perform the extra zero padding to make sure that the zero-parts can be exactly divided by non-zero parts, and then perform the iTV. Finally, we resize the reconstructed image to specified matrix size. Taking 60% zero padded case for example, the k-space includes 40% acquired data and 60% padded zeroes. To ensure the integer times zero padding, the extra 20% zeroes are padded to make sure that the zero-parts is 2 times of non-zero parts. After that, we divide the reconstructed oscillation pattern into 3 individual oscillation pattern where LSS is applicable. Finally, we resize the processed image to desired size. For comparisons, Hamming filter and LSS are performed on zero-padded case. The parameter of Hamming filter is experimentally chosen. The LSS is performed in two schemes. Scheme one directly performs LSS on image from zero-padded data, named LSS. Scheme two initially performs LSS on image reconstructed from non-zero parts data, and then resizes the processed image to required image size, named LSS + interpolation.

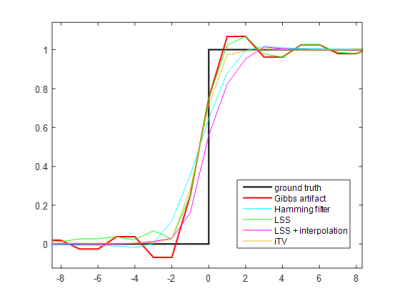
The simulated 1D stage and in vivo data are used to validate the effectiveness of the proposed method. The simulated stage contained 64 points with the value of zero and 64 points with the value of one. The in vivo T2WI and DWI data were acquired on 3T scanner (Achieva, Philips, Netherlands) and the acquisition parameters are as follows: for T2WI data, TR = 2000 ms, TE = 72 ms, resolution = 1 × 1× 4 $$$mm^{3}$$$, 60% zero padding along horizontal axis; for DWI, b=$$$1000s/mm^{2}$$$ , 4-shot EPI, TR = 3000 ms, TE = 82 ms, 50% zero padding along horizontal axis.

Results

The comparison between LSS and iTV is shown in Fig. 1. Fig. 1c shows that iTV produced less local total variation than LSS due to improved Gibbs artifact reduction. Fig. 2 presents the results of simulated 1D stage processed by different methods. The Hamming filter, LSS + interpolation and iTV all significantly suppressed Gibbs artifact than LSS, but iTV obtained sharper transition that are more close to the ground truth.

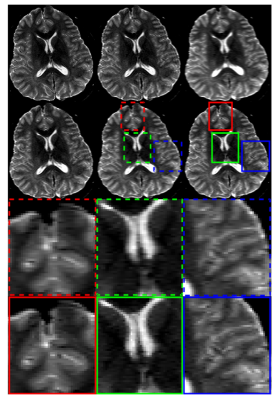
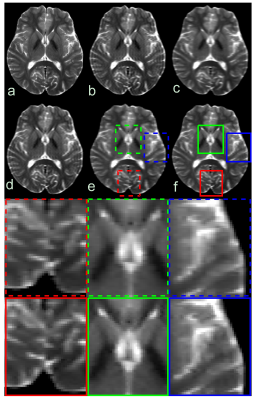
Figs. 3 and 4 show the results of DWI and T2WI data. The LSS failed to suppress the Gibbs artifact. Compared with LSS + interpolation, the proposed iTV method produced image with better preserved details.

Discussion and Conclusion

Acknowledgements

References

1. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts Magnetic Resonance in Medicine Volume 76, Issue 5. Magnetic resonance in medicine 2016;76(5):1574-1581.

2. Bella EVRD, Parker DL, Sinusas AJ. On the dark rim artifact in dynamic contrast-enhanced MRI myocardial perfusion studies Magnetic Resonance in Medicine Volume 54, Issue 5. Magnetic resonance in medicine 2005;54(5):1295-1299.

3. Ferreira P, Gatehouse P, Kellman P, Bucciarelli-Ducci C, Firmin D. Variability of myocardial perfusion dark rim Gibbs artifacts due to sub-pixel shifts. Journal of cardiovascular magnetic resonance : official journal of the Society for Cardiovascular Magnetic Resonance 2009;11-17.

4. Sharif B, Dharmakumar R, LaBounty T, Arsanjani R, Shufelt C, Thomson L, Merz CNB, Berman DS, Li D. Towards elimination of the dark-rim artifact in first-pass myocardial perfusion MRI Removing Gibbs ringing effects using optimized radial imaging, Magnetic Resonance in Medicine Volume 72, Issue 1. Magnetic resonance in medicine 2014;72(1):124-136.

5. Perrone D, Aelterman J, Pizurica A, Jeurissen B, Philips W, Leemans A. The effect of Gibbs ringing artifacts on measures derived from diffusion MRI. NeuroImage 2015;120:441-455.

6. Veraart J, Fieremans E, Jelescu IO, Knoll F, Novikov DS. Gibbs ringing in diffusion MRI. Magnetic resonance in medicine 2016;76(1):301-314.