4220

bin-SENSE: Accelerated MRI Near Metal With No Additional Hardware
Philip K. Lee1,2, Xinwei Shi1,2, Daehyun Yoon1, Evan G. Levine1,2, and Brian A. Hargreaves1,2

1Radiology, Stanford University, Stanford, CA, United States, 2Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

MAVRIC-SL suppresses artifacts induced by field inhomogeneities induced by metal, but requires increased scan time due to the acquisition of a fourth spectral dimension. We accelerate MAVRIC-SL acquisitions limited to the body coil by exploiting fieldmap information implicitly provided by the MAVRIC-SL acquisition. SENSE is applied to undo the coherent aliasing, using the spectral profiles as the spatial weights required for matrix inversion. A region growing method is applied to estimate the fieldmap and spectral profiles from uniformly undersampled data. We demonstrate 1.3x retrospective acceleration at a minimal g-factor penalty with no additional hardware requirement.

Introduction

MAVRIC-SL1 is a 3D multispectral sequence for imaging near metal. It acquires the volume with different spectral weightings, creating a fourth dimension referred to as bins. MAVRIC-SL suffers from increased scan times due to the acquisition of the additional bin dimension. Multiple methods have been applied to accelerate these scans, including compressed sensing2,3, parallel imaging, and partial Fourier sampling. In this work, we present a method for accelerating MAVRIC-SL scans where acquisition is restricted to the body coil. A retrospective study is presented to demonstrate the functionality of bin-SENSE.

Theory

While most methods undersample randomly in the $$$k_y-k_z$$$2, 3, 4 plane, our method undersamples uniformly in the $$$k_z$$$ dimension and exploits spatial variations between bins to resolve aliasing. Aliasing in the slice dimension can be resolved if the fieldmap is known. Using a spatial smoothness heuristic, the fieldmap is recovered from aliased data with a region-growing technique. We treat the bin-images as coil images and bin-profiles as coil sensitivities in a SENSE reconstruction5, shown in Figure 1. A retrospective acceleration factor of 1.3x is achieved. A quality reconstruction at an acceleration factor of 2x would be difficult to obtain using this method, as this reduces the size of the seed used for region-growing. Treating bin-images as coil-images has previously been presented, but undersampled lines were resolved using a GRAPPA-style kernel6.

Under the MAVRIC-SL Gaussian model, the spectral weighting of each bin can be converted to a spatial weighting $$$s(x,y,z,b)$$$ using equation (1) if $$$f_m(x,y,z)$$$, the fieldmap value, and $$$\sigma(x,y,z)$$$, the width, are known, where $$$f_b$$$ is the bin center frequency. For the unaliased volume, $$$f_m(x,y,z)$$$ and $$$\sigma(x,y,z)$$$ can be calculated by fitting a Gaussian along the bin dimension.

In the aliased region, the resulting bin profile is the summation of the bin profiles of the two aliasing slices. If the magnetization of the aliased slices was on-resonance, the bin profile will have two distinct Gaussian peaks at different center frequencies. For each aliased voxel, two Gaussians can be fit to the bin profile to recover two sets of candidate parameters $$$\Omega_1 : \{\rho_1, \sigma_1, f_1\}$$$, and $$$\Omega_2 : \{\rho_2, \sigma_2, f_2\}$$$. To recover the fieldmap, $$$\Omega_1$$$ and $$$\Omega_2$$$ must be assigned to the appropriate slice. This principle is illustrated in Figure 2. A region-growing algorithm that minimizes variations in the fieldmap is described in Figure 3. Bin parameters from the unaliased volume are used as the region-growing seed.

Using the recovered fieldmap and estimated spatial sensitivity, a SENSE reconstruction is performed, where the columns of $$$S$$$ are the bin-profiles of the aliased voxels.

$$s(x,y,z,b) = exp(- \frac{(f_m(x,y,z) - f_b)^2}{2\sigma(x,y,z)^2}) \hspace{2cm} (1)$$

Methods

A retrospective study was performed on subjects ($$$n = 7$$$) scanned on GE 3T MRI systems using a proton-density weighted MAVRIC-SL acquisition. The reference images for the retrospective study were reconstructed using l1-ESPIRIT7 in the Berkeley Advanced Reconstruction Toolbox8. The scan parameters were: 8-channel torso array, FOV = 40cm×40cm, in-plane matrix size = 384×256, slice thickness = 4mm, number of slices = 24, number of bins = 24, readout BW= 125 kHz or 0.65 kHz/pixel, 2×2 uniform undersampling and half-Fourier acquisition. Bin-SENSE was applied to reference images undersampled uniformly in the slice direction reducing the FOV by a factor of 2 resulting in 1.3x retrospective acceleration.

Results

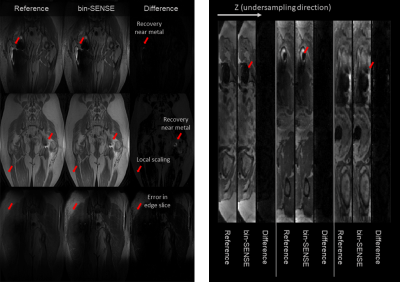
The recovered fieldmap was compared to the fieldmap derived from fitting a single peak model4 to the fully sampled dataset in Figure 4. Reconstructions from the 7 subjects using bin-SENSE are shown in Figure 5. The average structural similarity index (SSIM) values of bin-SENSE reconstructions compared to the reference dataset was 0.96 for aliased slices.

Discussion

The estimated fieldmap using region-growing shows good agreement with the reference fieldmap indicating that aliasing is correctly resolved. Due to the orthogonality of the bin profiles, the g-factor penalty is minimal. SSIM values between bin-SENSE and the fully sampled case demonstrate high reconstruction fidelity. Higher accelerations can be achieved but at the risk of unresolved aliasing particularly in regions of rapid field variation near the metal. Reconstruction errors can occur where the bin profile is not estimated properly. This method assumes that aliased voxels are mostly on-resonance, and that peaks of aliasing slices are separable along the bin dimension. This method faces difficulty where the Gaussian model does not hold. This occurs at edge slices where bin dimension profile forms a one-sided Gaussian due to the field of view in the slice direction not encompassing the object.

Conclusion

We have demonstrated a method for accelerating MAVRIC-SL acquisitions restricted to the body coil using prior knowledge of the fieldmap and a Gaussian spectral model.

Acknowledgements

R01 EB017739. GE Healthcare.

References

1. Koch K, et al. Imaging near metal with a MAVRIC-SEMAC hybrid. MRM. 2007;65(1):71-82.

2. Levine E, et al. Accelerated three-dimensional multispectral MRI with robust principal component analysis for separation of on- and off-resonance signals. MRM. 2017. DOI: 10.1002/mrm.26819.

3. Worters P, et al. Compressed-sensing multispectral imaging of the postoperative spine. JMRI. 2013;37:243-248.

4. Xinwei S, et al. Accelerated Imaging of Metallic Implants Using Model-Based Nonlinear Reconstruction. Proc. Intl. Soc. Mag. Reson. Med 24, 2016.

5. Pruessmann K, et al. SENSE: Sensitivity Encoding for FAST MRI. MRM. 1999;42:952-962.

6. Smith M, et al. Accelerating sequences in the presence of metal by exploiting the spatial distribution of off-resonance. MRM. 2014;72(6):1658-1667.

7. Uecker M, et al. ESPIRiT—an eigenvalue approach to autocalibration parallel MRI: where SENSE meets GRAPPA. MRM. 2014;71(3):990-1001.

8. Tamir J, et al. Generalized magnetic resonance image reconstruction using the Berkeley Advanced Reconstruction Toolbox. ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona 2016.

Figures

Figure 1. Relationship between bin-SENSE and the SENSE formulation. Left: SENSE resolves aliasing of the original volume (top) using prior knowledge of the coil’s spatial sensitivity (middle) and the measured aliased and weighted images (bottom). Right: In bin-SENSE, aliasing is resolved using the spatial weighting created by the spectral profile of each bin-image (middle), and the spatially weighted bin images (bottom).

Figure 2. The effect of undersampling on the fieldmap is demonstrated using a simulated dipole pattern. The fieldmap of the simulated slice (left) is undersampled in the direction creating an aliased replica (middle). The combination of the original and aliased replica is shown using horizontal symmetry (right), where the left and right halves are the unaliased and aliased slices respectively. The goal is to restore the original fieldmap using the parameter sets $$$\Omega_1:\{\rho_1,\sigma_1,f_1\}$$$, and $$$\Omega_2:\{\rho_2,\sigma_2,f_2\}$$$ calculated from undersampled data. Each $$$\Omega_1$$$, and $$$\Omega_2$$$ pair can be assigned to the correct slice using a region-growing technique.

Figure 3. Pseudo code for fieldmap estimation. Fieldmap estimation is divided into two parts: Gaussian model fit and region-growing. Region-growing algorithms are sensitive to local minima. To increase robustness to local minima, slices are dealiased in a middle-out scheme. This ensures that the comparison region is as close to the unaliased seed region as possible. At increased undersampling factors, the fieldmap estimation must extend further from the seed region, which leads to increased likelihood of incorrect fieldmap estimations.

Figure 4. Demonstration of fieldmap recovery using the region-growing technique. Example fieldmaps of an xy slice (a) and two yz slices (b) recovered using region-growing compared to fieldmaps estimated from bin-data prior to undersampling. Significant differences at the edges of the fieldmaps in the slice xy are due to voxels with no signal where the fieldmap is undetermined. The yz slices demonstrate effective recovery of the fieldmap in the on-resonance case, where the fieldmap increases linearly along the z dimension, and in the off-resonance case, where the fieldmap is distorted due to the metal.

Figure 5. Reconstructions using bin-SENSE. Left: Reconstructions in the xy plane show that bin-SENSE correctly resolves aliasing near the metal. An example of a reconstruction error occurring at the edge of the volume is shown (bottom). This artifact is caused by incorrect estimation of the Gaussian profile due to FOV truncation. Right: Reconstructions in the yz plane comparing bin-SENSE to the fully sampled data. Accurate recovery near metal is shown, with the location metal indicated by red arrows.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4220