4217
Fat Shift Correction in Bipolar Multi-Echo Dixon Imaging using Water-Fat Separation in k-Space1Philips Research, Hamburg, Germany
Synopsis
Fat is shifted relative to water in opposite directions in the odd and even single-echo images obtained with bipolar multi-echo sequences. Considering this effect in a water-fat separation permits suppressing associated artifacts, but has required regularization so far to cope with a locally ill-conditioned inverse problem in k-space. In this work, an alternative approach to limiting noise amplification in the water-fat separation is proposed and explored, which promises to avoid the loss of image sharpness observed with regularization.
Introduction
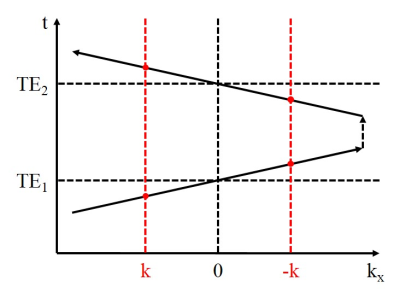
The use of bipolar multi-echo sequences for Dixon imaging poses several challenges to the water-fat separation. One of these is the misregistration between the odd and even single-echo images induced by chemical shift. It has been addressed previously by a water-fat separation in k-space which takes into account the actual acquisition times of the individual samples instead of the nominal echo times only.1 As illustrated in Fig. 1, this leads to a variable spacing of corresponding samples of the two echoes and deteriorates the condition of the occurring inverse problem locally. A suitable regularization is therefore required to prevent excessive noise amplification and coloring. The purpose of the present work is to explore an alternative approach to coping with an ill-conditioned water-fat separation in k-space.Theory
For the sake of simplicity, dual-echo Dixon imaging is considered in the following only. After estimation and demodulation of the main field inhomogeneity-induced phase from the single-echo images, the composite signal S in k-space is modelled by
$$\begin{bmatrix}S_{1k}\\S_{2k}\end{bmatrix} = \begin{bmatrix}1&c_{1k}\\1&c_{2k}\end{bmatrix} \begin{bmatrix}W_k\\F_k\end{bmatrix},$$
with
$$c_k=\sum_{n}w_n e^{2\pi i\Delta f_n t_k},$$
where W and F denote the water and fat signal in k-space, t the acquisition time, and w and Δf the relative amplitude and frequency of the peaks of the employed spectral model of fat. A solution for W and F is given by
$$\begin{bmatrix} W_{k}\\F_{k}\end{bmatrix} = (C_k^H C_k+\lambda I)^{-1} C_k^H\begin{bmatrix}S_{1k}\\S_{2k}\end{bmatrix},$$
with
$$C_k=\begin{bmatrix}1&c_{1k}\\1&c_{2k}\end{bmatrix},$$
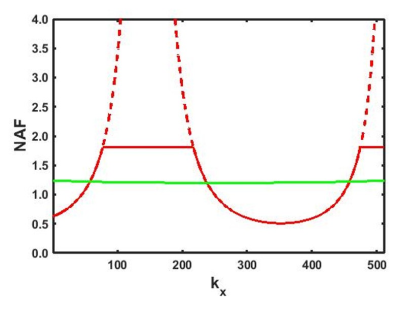
where λ denotes a regularization parameter. As demonstrated in Fig. 2, a suitable choice of λ allows to limit the noise amplification factor to a desired value. However, the diagonal loading of the matrix CHC introduces a bias in the water-fat separation. To avoid this, it is proposed to constrain the initial phase of the water and fat signal in image space to be equal whenever the condition of the matrix CHC is deemed too poor.2 The water and fat signal are then assumed to be real in image space, and thus to be Hermitian in k-space. Considering one echo only, S is described by
$$\begin{bmatrix}S_{k_1 R}\\S_{k_1 I}\\S_{k_2 R}\\S_{k_2 I}\end{bmatrix}=\begin{bmatrix}1&0&c_{k_1 R}&-c_{k_1 I}\\0&1&c_{k_1 I}&c_{k_1 R}\\1&0&c_{k_2 R}&c_{k_2 I}\\0&-1&c_{k_2 I}&-c_{k_2 R}\end{bmatrix}\begin{bmatrix}W_{k_1 R}\\W_{k_1 I}\\F_{k_1 R}\\F_{k_1 I}\end{bmatrix},$$
with
$$k_2=-k_1,$$
where R and I denote the real and imaginary part. Including the other echo as well leads to an overdetermined linear system of eight equations. W and F are, in both cases, derived as above, but without regularization.
Methods
Images of the pelvis of volunteers were acquired with a 3D T1-weighted spoiled dual-gradient-echo sequence on a 3 T Ingenia scanner (Philips Healthcare, Best, The Netherlands) using anterior and posterior coil arrays. A FOV of 350 (AP) x 350 (RL) x 200 (FH) mm3, a resolution of 0.7 x 0.7 x 2.5 mm3, a TE1/TE2/TR of 2.0/3.7/5.5 ms, and a flip angle of 10° were chosen. The pixel bandwidth amounted to 650 Hz, corresponding to a shift of the signal from the dominant peak of the fat spectrum of 0.65 pixel in the single-echo images.
The main field inhomogeneity-induced phase and the initial phase of the water and fat signal were first determined and eliminated from the single-echo images, ignoring any misregistration.3 The original complex two-point separation, without and with regularization, as well as the proposed hybrid complex-real two-point separation without regularization were then applied in k-space.
Results
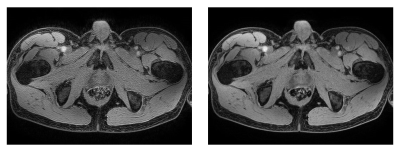
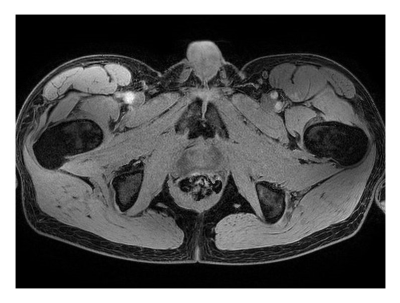
The basic feasibility of keeping the water-fat separation well-conditioned without regularization with the described approach is shown in Fig. 2. The noise amplification factor, calculated for a phase-constrained one-point separation based on the first echo in this case, exhibits only minor variations across k-space and remains within reasonable bounds. While regularization is essential with the original complex two-point separation to prevent high frequency noise from breaking through, as evident from Fig. 3, it is unneccessary with the proposed approach. This is exemplified in Fig. 4 using a phase-constrained two-point separation.Discussion
It has been noted previously that regularization in the original complex two-point separation leads to a loss of spatial resolution.1 The proposed approach promises to avoid this without suffering from excessive noise amplification. A close inspection of the images obtained so far suggests that image sharpness is indeed increased in some of the structures. However, the proposed approach also seems to be more susceptible to errors in the phase estimation, which manifests itself in artifacts at some of the interfaces. Further work will attempt to improve it and will investigate in more depth the trade-off between spatial resolution, noise amplification, and image artifacts.Acknowledgements
No acknowledgement found.References
1. Lu W, et al. Magn Reson Med 2008; 60:198-209. 2. Bydder M, et al. Magn Reson Imaging 2011; 29:216-221. 3. Stinson EG, et al. Magn Reson Med 2017; Early View.Figures