4211

Reduction of artefacts in Bloch-Siegert based $$$B_1^+$$$-Mapping in CPMG-Sequences with imperfect refocussing pulses
Volker JF Sturm1,2, Thomas Kampf3,4, Lukas R Buschle2, Ke Zhang2, Peter M Jakob4, Mirko Pham3, Christian Ziener2, Martin Bendszus1, Sabine Heiland1, and Felix T Kurz1,2

1Experimental Neuroradiology, University Hospital Heidelberg, Heidelberg, Germany, 2German Cancer Research Center, Heidelberg, Germany, 3Diagnostic and Interventional Neuroradiology, University Hospital Würzburg, Würzburg, Germany, 4Experimental Physics V, University Würzburg, Würzburg, Germany

Synopsis

The Bloch-Siegert-effect imprints the rf-coil’s transmission field in the phase of the acquired signal. Consequently the measured amplitude information can be used to determine other MR-Parameter. A previously published sequence based on a CPMG spin echo train uses both information pathways and allows simultaneous acquisition of $$$T_2$$$- and $$$B_1^+$$$-maps. However, the formerly proposed method produces potentially erroneous $$$B_1^+$$$-map in inhomogeneous $$$B_0$$$-fields.

This work presents a method to reduce those errors by combining signal from different echoes. This allows a robust measurement of $$$B_1^+$$$-maps in inhomogeneous $$$B­_0$$$-fields as present in high-field MRI with simultaneous $$$T_2­$$$ quantification.

Introduction

For quantitative MRI it is important to determine the $$$B_1^+$$$-field of the transmission rf-coil. That allows to correct the impact of mismatched flip angles during the measurement on the magnetization evolution. One possibility to obtain the transmission field is based on the Bloch-Siegert effect1. This effect allows to encode the $$$B_1^+$$$-information into the signal phase while at the same time the signal amplitude is practically maintained. This allows the acquisition of the $$$B_1^+$$$-field simultaneous with other MR parameters encoded in the signal magnitude. This was shown for $$$T_2$$$ quantification using a CPMG spin-echo train2. However for imperfect refocusing pulses the signal phase of off-resonant spins is not constant in the echo train. Consequently the use of phase information from different echoes may result in erroneous $$$B_1^+$$$ values. In this work a method to minimize those errors is presented.

Material and Methods

By applying off-resonant rf-pulses with $$$\omega_{off}\gg{\gamma}B­_1^+$$$ and $$$\omega_{off}\gg\Delta\omega_0$$$ the phase of the transversal magnetization is changed by:

$$\Phi_{BS}[\omega_{off}]\approx\frac{({\gamma}B_1^+)^2}{2\omega_{off}}\left(1-\frac{\Delta\omega_0}{\omega_{off}}\right)$$

while the magnitude is not influenced. Whereby the off-resnonance of the rf-puls is given by $$$\omega_{off}$$$ and the frequency shift caused by the $$$B_0$$$-field inhomogeneity by $$$\Delta\omega_0$$$. By taking the phase difference $$$\Delta\Phi$$$ of two measurement with alternated sign of $$$\omega_{off}$$$ $$$B_1^+$$$ can be calculated by1

$$B_1^+\approx\sqrt{|\Delta\Phi\,\omega_{off}|}/\gamma.\hspace{5em}(1)$$

Therefore it is essential that $$$\Delta\Phi$$$ is solely determined by the Bloch-Siegert effect. A published method2 for simultaneous measurement of $$$T_2$$$ and $$$B_1^+$$$ compares phase information taken at different echo times. However it can be shown3, that the phase for the magnetization in the nth echo of a CPMG echo train is given by:

$$\Phi_{CPMG}[n]\approx -\frac{n}{4}(-1)^n(\pi-\alpha)^2\sin[\Delta\omega_0{T\!E}].$$

It can be seen, that for imperfect refocusing pulses ($$$\alpha\neq\pi$$$) the phase amplitude for offresonant magnetization increases linear with echo number while the sign alternates. Consequently in the phase difference $$$\Delta\Phi$$$ of two echos with alternated $$$\omega_{off}$$$ sign but different echo number the term $$$\Phi_{CPMG}$$$ is not fully cancelled so that by using equation (1) erroneous $$$B_1^+$$$-values are produced. However based on the character of this phase variation it is possible to choose echo number combinations so that both BS-encodings have the same mean phase offset $$$\Phi_{CPMG}$$$. For example using the mean phase from the first and fifth echo (both with positive BS-encoding) minus the third echo (negative BS-encoding) produce:

$$\Delta\Phi=\frac{\Phi_{BS}[\omega_{off}]+\Phi_{BS}[\omega_{off}]}{2}+\frac{\Phi_{CPMG}[1]+\Phi_{CPMG}[5]}{2}-\Phi_{BS}[-\omega_{off}]-\Phi_{CPMG}[3]\\=\Phi_{BS}[\omega_{off}]-\Phi_{BS}[-\omega_{off}].$$

Accordingly the term $$$\Phi_{CPMG}$$$ is removed and $$$\Delta\Phi$$$ now depends solely on the Bloch-Siegert phase difference even though different echo numbers were used.

Results

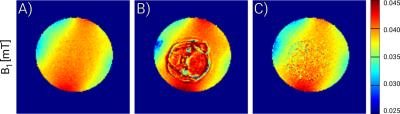
In figure 1 different $$$B_1^+$$$-maps are shown which are measured with a linear birdcage coil. The Bloch Siegert encoding was integrated in a CPMG spin echo sequence as descriped in 2. As reference figure 1A) shows the $$$B_1^+$$$ map calculated from two consecutive measurements (effectively doubeling the measurement time). Hence, for all echo times both BS-encodings are existent and $$$\Phi_{CPMG}$$$ is cancelled in the $$$B_1^+$$$ calculation. For figure 1B) and C) both BS-encodings are acquired in a single echo train using the ($$$++--$$$) BS-encoding scheme2. For figure 1B) the $$$B_1^+$$$-calculation as described in 2 was used. By calculating $$$B_1^+$$$ values based on phase information from different echo times significant deviation can be seen in comparison to figure 1A). Those errors arising from $$$\Phi_{CPMG}$$$ can be almost removed by the presented improved $$$B_1^+$$$-calculation (figure 1C) using the same measured data as in figure 1B). Since only half of the measurement time is needed for the data acquisition for figure 1B) and C) the noise level in those maps is slightly increased in comparison to figure 1A). Therefore the adapted data evaluation allows reliable quantification of $$$B_1^+$$$ using only a single CPMG spin echo train.

Discussion and Conclusion

The $$$B_1^+$$$ measurement based on the Bloch Siegert effect is robust to biases caused by several MR parameters like $$$T\!R$$$, $$$T_1$$$ and magnetization transfer. Moreover, since the Bloch-Siegert effect does not alter the signal magnitude, simultaneous quantification of further MR parameter is possible. However, this thrilling potential, to quantify $$$T_2$$$ and $$$B_1^+$$$ simultaneous, was not universal applicable until now. Based on the fact, that only the $$$B_1^+$$$ calculation has to be adapted, it can be also used to improve already measured data.

Acknowledgements

F.T.K. was supported by a postdoctoral fellowship from the medical faculty of Heidelberg University, the Hoffmann-Klose Foundation (Heidelberg University), and a grant from the Deutsche Forschungsgemeinschaft (Contract Grant No.: DFG KU 3555/1-1). C.H.Z., K.Z. and L.R.B. were supported by a grant from the Deutsche Forschungsgemeinschaft (Contract grant number: DFG ZI 1295/2-1).

References

1. Sacolick Li, Wiesinger F, Hancu I, Vogel MW. $$$B_1$$$ mapping by Bloch-Siegert shift. Magn Reson Med. 2010;63:1315-1322.

2. Sturm VJF, Basse-Lüsebrink TC, Kampf T, Stoll G, Jakob PM. Improved encoding strategy for CPMG-based Bloch-Siegert $$$B_1^+$$$ mapping. Magn Reson Med. 2012;68:507-515.

3. Bain AD, Anand CK, Nie Z. Exact solution of the CPMG pulse sequence with phase variation down the echo train: Application to $$$R_2$$$ measurements. Journ Magn Reson 2010;209:183-194.

Figures

Figure1: Calculated $$$B_1^+$$$-maps of a birdcage coil measured using a CPMG sequence. The also acquired $$$T_2$$$-maps are not shown. A) Reference $$$B_1^+$$$-map calculated using two measurements - identical except for the used BS-puls offset sign. B) $$$B_1^+$$$-map calculated from only one measured echo train with both BS-encoding signs using the evaluation published in 2. C) $$$B_1^+$$$-map calculated from only one measured echo train with both BS-encoding signs using the proposed processing to remove $$$\Phi_{CPMG}$$$. Since only half of the measurement time is needed for the data acquisition for figure 1B) and C) the noise level in those maps is slightly increased.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4211