4203
Image Distortion Correction via Gradient Nonlinearity Encoding at 9.4T MRI with Radial Ultra short TE (UTE) Sequence1The University of Queensland, Brisbane, Australia
Synopsis
Radial-encoding sequences can be more sensitive to gradient trajectory deviations caused by gradient nonlinearity (GNL) than Cartesian encoding. In this work, we developed a method to alleviate image distortion caused by GNL specifically for radial-encoding. Experimental results acquired from a 9.4 T pre-clinical MRI scanner with using Ultra-short TE sequence were used to validate the proposed method.
Introduction
Due to design and construction limitations, gradient nonlinearity (GNL) could deviate actual k-space trajectories from nominal ones, undermining orthogonality of Fourier encoding and producing images with blurring, ghosting artifacts and increased noise 1. These image distortions could be more dramatic when using radial sequences, which require accurate gradient trajectories for image reconstruction with regridding 2 or filtered back-projection 3. Various methods have been developed to correct GNL-induced image distortions. The field camera 4 measures actual field spatiotemporal profile used for image reconstruction and correction 5. Non-uniform Fourier transform (NUFFT) is employed to realise integrated GNL correction during image reconstruction 6. Parametric models of gradient waveforms with multiple functions can be built for trajectory correction 7. In this work, like SENSitivity Encoding (SENSE) 8, we considered “GNL radial encoding” as a special encoding superimposed on standard Fourier encoding. The proposed method was tested on in vivo mice brain images acquired from a 9.4T pre-clinical MRI scanner with using Ultra-short TE (UTE) sequence. Primary results demonstrated that the method was capable of dramatically reducing image distortion caused by GNL.Methods
The forward process of acquiring a radial k-space $$${b_{radial}}$$$can be expressed as:$${F_{radial}x=b_{radial}} \tag{1a}$$where$$${F_{radial}}$$$denotes non-distorted radial Fourier encoding matrix, in which each element is a radial Fourier kernel in the form of$$${e_{k,r}=e^{-2\pi jk_{radial}r}}$$$. $$${k_{radial}}$$$is the radial k-space locations and r is the voxel locations of imaging subject x. When the GNL occurs, it resides in the forward encoding process and the Eq.1a can be modified to:$${E_{GNL}\cdot F_{radial}x=b_{radial}} \tag{1b}$$where$$$ {E_{GNL}}$$$denotes the GNL encoding in the form of $$${e_{k,r}^{GNL}=e^{-2\pi j{\triangle k_{radial}}r}}$$$. $$${\triangle k_{radial}}$$$ is the radial trajectory deviation caused by GNL. The image x can be recovered by minimising the following function$${\parallel E_{GNL}\cdot F_{radial}x-b_{radial}\parallel_{2}\tag{2} }$$The experiments were performed on a 9.4T Bruker Biospin MRI scanner (Ettlingen, Germany). A surface coil (Ø: 40 mm) with 60° open angle and 26 mm length was used to acquire in vivo mouse brain images. The TE and TR of the UTE sequence was set as 0.4ms and 100ms. Paravision 6 provided radial trajectory locations which were used for the proposed method to correct image distortion.Results
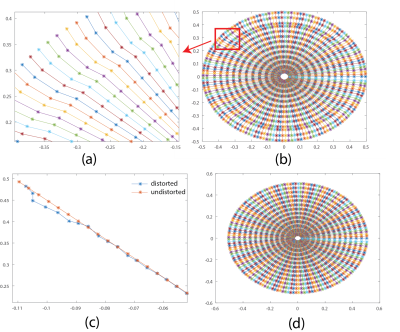
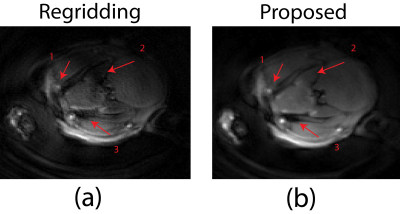
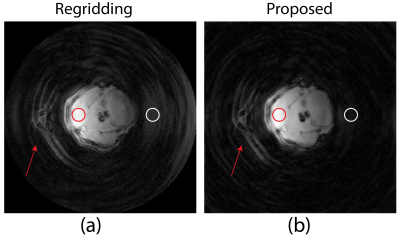
The k-space trajectories of the UTE sequence exported from Paravision 6 with and without GNL distortion are shown in Fig. 1b and Fig. 1d, respectively. As showed in Fig. 1a and c, trajectory errors occurred at various parts of radial spokes, especially outer region of the k-space, which potentially result in resolution loss and undesired noise. With such deviated radial trajectories, images reconstructed from routine algorithms such as regridding are incapable of removing these artifacts as demonstrated in Fig. 2a. The blood vessel (arrow 1) which is vague becomes more visible in Fig.2b after applying the proposed GNL correction method, despite it being distant to the surface coil. Severe signal loss (arrow 2) observed in Fig. 2a was well compensated with the proposed method as indicated by Fig. 2b. The low proton density area marked with red arrow 3 in Fig. 2a is seriously contaminated with ghost artifacts, which are later eliminated with the proposed method and the boundary between different tissues is more distinct. Fig. 3b is the image reconstructed by the proposed method. Compared to Fig. 3a without GNL correction, the background noise was substantially reduced and the image quality was greatly increased. Specifically, the noise (white circular region) in Fig. 3b was reduced to 0.0011, which is 38% of uncorrected image (0.0029). The SNR (calculated with NEMA standard 9) of GNL-corrected image has a 2.6-fold increase from 186.7 (Fig. 3a) to 483.9 (Fig. 3b). Details at tissues boundaries are also well preserved.Discussion
The proposed method employs GNL encoding concept to correct image distortion during image reconstruction process. Formula 2 was iteratively solved by using Matlab function lsqr. Through the iterative optimisation process, the proposed method is expected to reduce more GNL distortions than the regridding method when inaccurate k-space trajectory information is acquired. The construction of GNL encoding and Fourier encoding matrix is computationally expensive, which shall be handled with a more efficient optimization algorithm in the future.Conclusion
An image distortion correction method based on GNL radial encoding was proposed. This method superimposes the GNL encoding onto the standard radial encoding, so that the image can be reconstructed with reduced artifacts through an iterative optimisation process. In vivo experiments performed on a 9.4 T pre-clinical system showed that the proposed method is capable of effectively correcting the GNL-induced distortions and thus improve the image quality. In the future, the proposed algorithm will be enhanced for wider MRI applications such as spiral imaging.Acknowledgements
No acknowledgement found.References
1. Janke A, Zhao H, Cowin GJ, Galloway GJ, Doddrell DM. Use of spherical harmonic deconvolution methods to compensate for nonlinear gradient effects on MRI images. Magn Reson Med 2004;52:115-122.
2. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magnetic resonance in medicine 2007;57:1086-1098.
3. Lauterbur PC, Liang Z. Principles of Magnetic Resonance Imaging: IEEE Press, New York, NY, USA, 2000.
4. Dietrich BE, Brunner DO, Wilm BJ, et al. A field camera for MR sequence monitoring and system analysis. Magnetic resonance in medicine 2016;75:1831-1840.
5. Tao S, Trzasko JD, Gunter JL, et al. Gradient nonlinearity calibration and correction for a compact, asymmetric magnetic resonance imaging gradient system. Phys Med Biol 2017;62:N18-N31.
6. Tao S, Trzasko JD, Shu Y, et al. NonCartesian MR image reconstruction with integrated gradient nonlinearity correction. Medical physics 2015;42:7190-7201.
7. Takizawa M, Hanada H, Oka K, Takahashi T, Yamamoto E, Fujii M. A robust ultrashort TE (UTE) imaging method with corrected k-space trajectory by using parametric multiple function model of gradient waveform. IEEE Trans Med Imaging 2013;32:306-316.
8. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine 1999;42:952-962.
9. Sano R. NEMA standards: Performance standards for clinical magnetic resonance systems. RL Dixon 1988:185-189.
Figures