4176
Automatic Generation of Topologically Correct, High Quality, Finite-Element Tetrahedral Body Models from Voxel and Surface Data1Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany, 2Martinos Center for Biomedical Imaging, Dept. of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Harvard-MIT Division of Health Sciences and Technology, Cambridge, MA, United States
Synopsis
Assessment of MR safety, e.g., Specific Absorption Rate (SAR) and Peripheral Nerve Stimulation (PNS), relies on the accurate estimation of electromagnetic fields in complex human body models. Finite Element Methods (FEM) can use tetrahedral meshes that can model curved geometries much more accurately than voxel-based meshes. The creation of high-quality surface body models (needed to generate tetrahedral meshes), however, is complex due to the requirements for the surface models (water-tightness, correct topology, no intersections, etc.). We developed an automatic pipeline that, starting with arbitrary surface and voxel data, generates high quality, watertight, topologically correct surface models to be practically useful in FEM simulations.
Target audience
MRI electromagnetic modelers, MR safety
researchersPurpose
To develop and disseminate a processing pipeline for generation of surface (triangles) and volume (tetrahedrons) mesh body models. The models generated are well suited for electromagnetic simulations (e.g., using CST, Ansys HFSS etc.) as they are (i) spatially adaptive; (ii) topologically correct; (iii) allow modeling of multiple adjacent tissues without intersections, (iv) are of high-quality, and (v) have reasonably low number of faces.Introduction
Assessment of MR safety heavily relies on the accurate estimation of electromagnetic (EM) fields in complex human body models. This includes assessment of the specific absorption rate (SAR)1,2 and peripheral nerve stimulations (PNS) from switching gradients3. Finite Element Methods (FEM) can use tetrahedral meshes that are better adapted to modelling of curved geometries and widely varying spatial scales within the same domain than voxel-based discretization. However, robust generation of high-quality surface models (which are needed to generate tetrahedral meshes) is complex because of a large variety of possible topology problems such as lack of water-tightness, face intersections, and non-manifold geometries. Most previously proposed methods for surface model generation use marching cubes techniques4 that generate surface models with huge number of faces and, therefore, are often impractical for FEM simulations.Methods
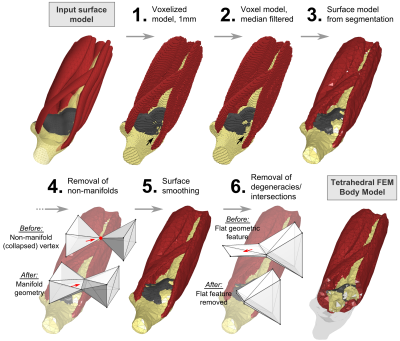
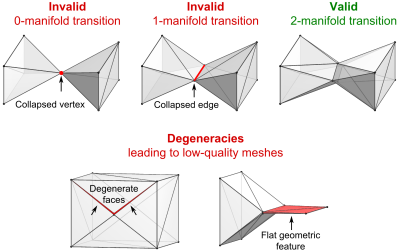
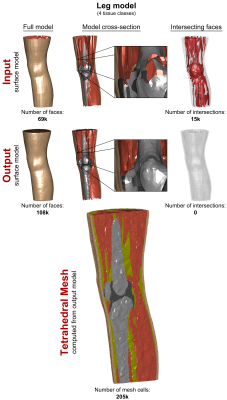
The processing steps of our pipeline are depicted in Fig. 1. Choice of input data: Our method works for both surface- and voxel-based inputs. Surface inputs do not have to be topologically corrected and may have intersecting objects. Voxel data may include existing voxel models or new models based on MRI or CT segmentations. (1) Surface Voxelization: If a surface model is used as the input, the surface objects (i.e., tissue classes) are closed and discretized on a Cartesian grid, yielding a solid voxel model. The resolution of the discretization is chosen by the user (1 mm is adequate for most body and brain structures). (2) Voxel Model Simplification: Depending on the required spatial resolution of the surface models, the voxel model is simplified, e.g., using a morphological median filter (the level of simplification is controlled by the kernel size and the number of repetitions). This removes small geometric features and thin tissue layers. (3) Surface-Segmentation of Voxel Model: The final voxel model is used as input to a surface-based segmentation (CGAL5) that generates watertight non-intersecting surfaces that separate the different tissue classes. The spatial accuracy of the segmentation (and thus the number of faces in the final model) can be adjusted within CGAL (e.g., the smallest allowed face area). (4) Removal of Non-Manifold Features: The surface model created by CGAL may have non-manifold “unphysical” features, i.e., features that collapse to a single vertex (“0-manifold”) or single edge (“1-manifold”), see Fig. 2, top. We repair these violations (code implemented in Matlab) by first deleting the faces corresponding to manifold errors, which creates holes in some tissue classes. Second, we identify possible face configurations to close these holes without causing new surface errors. (5) Surface Smoothing: The previous voxelization and segmentation steps may create unwanted jags or edged geometric features, which we remove using Laplacian smoothing6. (6) Removal of Low-Quality Faces: We remove surface features which are hard to mesh, in particular “degenerate faces” (i.e., extremely “sharp” faces) and face pairs that enclose an angle close to zero (the faces almost intersect), see Fig. 2, bottom. This is done by deleting the affected faces and closing the resulting surface holes as described in Step 4. (7) Repairing Intersections: We check if the surfaces intersect using the freely available Tetrahedral Mesh Generator, TetGen7. Existing intersections are removed using the workflow described in Step 4. Evaluation: We generated surface body models from three body regions (head, abdomen, knee) of the Zygote (American Fork, UT, USA) anatomical models. These models have been developed for visualization/teaching and, therefore, cannot readily be used for FEM simulations. The processing pipeline was adjusted to generate models with reasonable balance between anatomical accuracy and mesh complexity (i.e., face number).Results
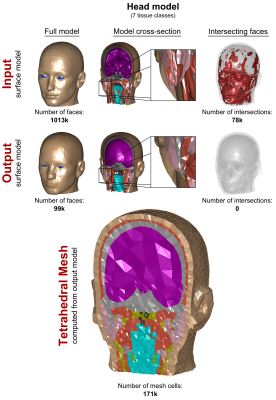
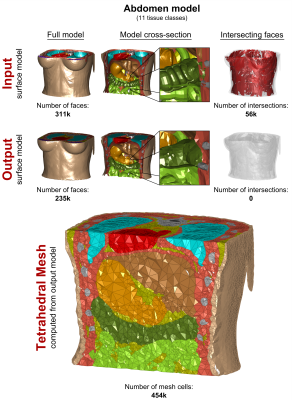
In Figs. 3, 4, and 5, we show the input “corrupt” surface models (1st row) and the repaired output models (2nd row) in terms of the full model (left), cross-section (center), and face intersections (right). Exemplary tetrahedral meshes for each body region computed from the repaired models are shown at the bottom. Our voxelization/segmentation approach generates surface models that properly approximate the input models while simplifying the geometry to reduce the complexity (the level of simplification can be controlled by the user). Computation took approximately 1h per model. All models could be imported and meshed without any errors in CST and HFSS.Acknowledgements
No acknowledgement found.References
[1] Kozlov et al., "Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation." Journal of Magnetic Resonance 200(1): 147-152, 2009
[2] Guérin et al., "Comparison of simulated parallel transmit body arrays at 3 T using excitation uniformity, global SAR, local SAR and power efficiency metrics." Magnetic Resonance Imaging 73(3): 1137-1150, 2015
[3] Davids et al., “Predicting magnetostimulation thresholds in the peripheral nervous system using realistic body models”, Sci. Rep. 7:5316, 2017
[4] Raman et al., “Quality Isosurface Mesh Generation Using an Extended Marching Cubes Lookup Table”. Computer Graphics, 27(3):791-798, 2008
[5] The CGAL Project. CGAL User and Reference Manual (CGAL Editorial Board), 4.9 edn., 2016
[6] Bade et al., "Comparison of Fundamental Mesh Smoothing Algorithms for Medical Surface Models", Simulation and Visualization, pp. 289-304, 2006
[7] Si et al., "TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator". ACM Transactions on Mathematical Software, 41(2), 2015
Figures