4175

Simulation of Peripheral Nerve Stimulation Thresholds of MRI Gradient Coils
Mathias Davids1,2, Bastien Guérin2,3, Valerie Klein1, Lothar R Schad1, and Lawrence L Wald2,3,4

1Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany, 2Martinos Center for Biomedical Imaging, Dept. of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Harvard-MIT Division of Health Sciences and Technology, Cambridge, MA, United States

Synopsis

Peripheral Nerve Stimulation (PNS) has become the major limitation in many fast MRI sequences for state-of-the-art gradient systems. We recently presented the first (to our knowledge) full peripheral nerve model for assessing magnetostimulation thresholds and validated it for solenoid coils. Our model consists of a comprehensive body model for EM simulations, a detailed atlas of human nerve fibers, and a numerical model describing nerve responses to induced electrical fields. Here, we extend our approach to realistic MRI gradient coils in simulations of male and female body models. The average threshold closely matches experimentally obtained group PNS threshold curves.

Target Audience

MR safety researchers, MRI gradient designers, MR engineers

Purpose

As the performance of MRI gradient systems improves, Peripheral Nerve Stimulation (PNS) is becoming the major limitation in many MRI sequences1,2. Rapid switching of MRI gradient coils induces E-fields in the body powerful enough to stimulate nerves. In MRI, PNS thresholds are usually characterized as the smallest gradient amplitude at a given rise-time (in a trapezoidal readout) that causes PNS. These PNS threshold curves are obtained experimentally after coil construction, but efforts to numerically simulate PNS in realistic coils has recently been initiated3,4,5. Here we present the first attempt of predicting PNS thresholds for gradient coils using a comprehensive whole-body nerve model and show that the predicted thresholds are in close agreement with measured population averages.

Methods

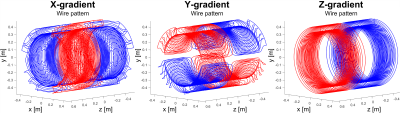
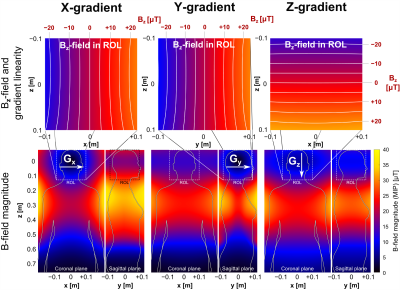
PNS Simulation Framework: Simulations were done on both a male and female body model with the head at isocenter. Our PNS threshold simulation has three major components: 1) detailed female and male body models (surface meshes) for simulation of the induced EM-fields, 2) detailed nerve atlases registered to the body model. For each nerve, we labeled the fiber diameter by a look-up table, 3) a previously validated neurodynamic model for mammalian nerves (MRG)6 to simulate the generation of action potentials (AP) by the induced E-field. Knowing the induced E-fields, we project the E-field onto the nerve fibers and integrate along the fiber paths to determine the relevant electric potential change. Note, that this potential is temporally modulated by the coil’s driving waveform and thus changes in both space and time. The threshold for a given drive waveform is obtained by increasing the waveform amplitude until an AP is created (titration). This process is repeated for different modulation frequencies of trapezoidal and sinusoidal waveforms. The threshold curve is plotted as the gradient amplitude, which first produces stimulation as a function of the rise-time (“pulse duration”). Gradient Coils: We simulated PNS thresholds for the 3 axes of the Siemens Sonata whole body gradient coil (Fig. 1) with known experimental PNS thresholds (averaged over 65 healthy adult subjects7). In both simulation and experiment, the head was placed at isocenter. E-fields were calculated using a hexahedral magneto-quasi-static FEM solver (Sim4Life, Zurich MedTech, Switzerland) using isotropic 1 mm resolution and tissue parameters from the Gabriel database8. Evaluation: We generated PNS threshold curves using sinusoidal and trapezoidal ramp times between 100 us and 1000 us, using a 500 us constant flat top duration between the ramps. Both single “Y” gradient axis operation and combined axes operation (“X-Y”, “X-Y+Z”) were simulated. For the single “X” and “Z” gradient axes, the experimental setup could not generate stimulation.

Results

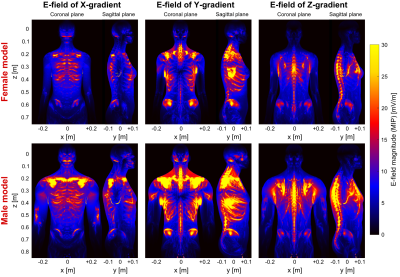
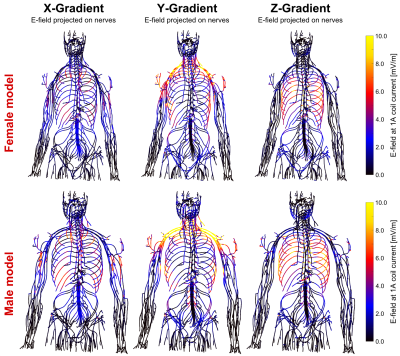
Figures 1 and 2 show the winding patterns and simulated magnetic fields of the gradient coils. All coils produce substantial concomitant B-fields in the abdominal region (0.1 m < z < 0.5 m). Figure 3 shows the E-field induced in the two body models by a 1 A, 1 kHz sinusoidal current. The regions of significant E-field strength mostly coincide with regions of highest magnetic field strength (0.1 m < z < 0.5 m) but are highly shaped by the conductive tissues. Figure 4 shows the magnitude of the E-field projected onto the nerve paths. This entity determines the amount of axial current flowing in the nerve fiber. For both body models, the Y-gradient causes the largest axial current flow, followed by the Z-gradient and the X-gradient.

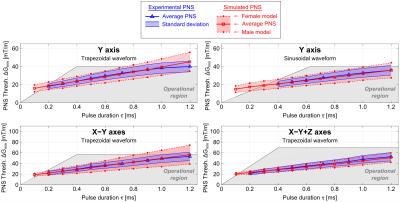
Figure 5 shows experimental thresholds (blue curve, with measurement SD over all subjects in blue shaded region) and the simulated PNS thresholds (top curve: female, bottom curve: male, center curve: average). The gray shaded region is the experimentally accessible region. There is good agreement between experimental and simulated PNS threshold curves: the NRMSE between average experimental and simulated thresholds is 4.4% and 2.5% for the Y-axis (trapezoidal and sinusoidal waveform, respectively), 3.8% for the "X-Y" axes and 5.6% for the "X-Y+Z" axes (both for trapezoidal waveforms). The gender differences likely result from body size differences and fat content differences (the nerves tend to run in the fat between muscles), although more work is needed to investigate this effect.

Conclusion

We show it is possible to accurately predict group-average experimental PNS thresholds of a specific MRI gradient coil, although a single body model was not sufficient; representation of both genders was needed. We hope that such a simulation framework will allow gradient design modifications to be tested prior to construction, with an ultimate goal of improving what has become the major limitation to applying stronger MRI gradients in humans

Acknowledgements

We thank Eva Eberlein and Franz Hebrank of Siemens for detailed information and guidance on the gradient coils.

NIH grants: K99/R00 EB019482, P41EB015896, U01EB025121, U01EB025162

References

[1] McNab et al., "The Human Connectome Project and beyond: Initial applications of 300 mT/m gradients". NeuroImage 80, 2013

[2] Setsompop et al., "Pushing the limits of in vivo diffusion MRI for the Human Connectome Project". NeuroImage 80, 2013

[3] Neufeld et al., "Functionalized anatomical models for EM-neuron Interaction modeling". Phys. Med. Biol. 61(12), 2016

[4] Davids et al., “Modeling of Peripheral Nervous Stimulation Thresholds in Realistic Body Models”, Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, 2017

[5] Davids et al., “Predicting magnetostimulation thresholds in the peripheral nervous system using realistic body models”, Sci. Rep. 7:5316, 2017

[6] McIntyre et al., “Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle”. J Neurophysiol. 87(2), 2002

[7] Hebrank et al., "SAFE model -- a new method for predicting peripheral nerve stimulation in MRI”. Proceedings of the 8th Annual Meeting of ISMRM, Denver, USA, 2000

[8] Gabriel et al., “The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues”. Phys. Med. Biol. 41, 1996

Figures

Figure 1: Wire patterns of the actively shielded whole-body MRI gradient coil investigated in this work (a Siemens “Sonata” whole-body gradient). The coils can generate a gradient field of 40 mT/m at a slew rate of 200 T/m/s.

Figure 2: Magnetic fields produced by the gradient coils at 1 A applied current: the top row shows the Bz-field produced in the region-of-linearity (dashed lines in the bottom plots). The iso-contour lines are spaced at 5 µT. The bottom row shows the maximum intensity projection of the B-field magnitude in the coronal (left sub-panel) and sagittal (right sub-panel) plane.

Figure 3: Electric fields (maximum intensity projection) induced in the female body model (top row) and the male body model (bottom row). The EM-field simulation was performed at 1 mm isotropic resolution, using a coil current of 1 A modulated by a 1 kHz sine wave.

Figure 4: Magnitude of the E-field projected onto the nerve fibers (i.e., the E-field pointing along the direction of the nerve fiber path). This field component determines the amount of current flowing in the axial direction of the nerve fiber.

Figure 5: Simulated PNS thresholds (red, for female/male body model and average) and experimental PNS thresholds (blue, including standard deviation over all subjects) in terms of the minimum gradient magnitude ΔGmin as a function of the pulse duration τ that caused PNS. The top row shows the “Y” axis results for trapezoidal (left) and sinusoidal waveforms (right). The bottom row shows PNS threshold curves for the "X-Y" and "X-Y+Z" axes combinations (both for trapezoidal waveforms).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4175