4151

Motion Prediction using a Multi-Rate Kalman Filter with Golden Angle Radial Acquisition for Real-Time MRI-Guided Interventions
Xinzhou Li1,2, Samantha Mikaiel1,3, and Holden H. Wu1,2,3

1Radiological Sciences, University of California, Los Angeles, Los Angeles, CA, United States, 2Bioengineering, University of California, Los Angeles, Los Angeles, CA, United States, 3Physics and Biology in Medicine, University of California, Los Angeles, Los Angeles, CA, United States

Synopsis

Real-time MRI can provide high soft-tissue contrast without ionizing radiation for interventional procedure guidance. To achieve accurate and low-latency tracking of target tissues for decision support and feedback control, this work proposes a motion prediction framework based on a multi-rate Kalman filter and real-time golden-angle radial MRI. The proposed framework leverages the unique sampling pattern of golden-angle radial acquisition to combine image-based with surrogate-based motion tracking. Initial results demonstrate that the proposed framework can achieve significantly reduced error in motion prediction and provide low-latency feedback for real-time MRI guided interventions.

Introduction

Remotely controlled instruments improve access to patients for real-time MRI guided interventions1; however, intra-procedural gating or tracking for feedback control of these instruments often suffer from inaccurate motion tracking and/or system latency2,3. Image-based tracking achieves high spatial accuracy, but introduces additional latency. Surrogate-based tracking achieves low latency, but often has reduced spatial accuracy and requires external measurement systems or markers4.

In this study, we propose a multi-rate motion prediction framework that combines the respective advantages of image-based and surrogate-based tracking. This was achieved by leveraging the golden-angle (GA) radial trajectory to simultaneously reconstruct images and extract surrogate signals from the same data stream5. Image-based and surrogate-based tracking results were fused in a multi-rate Kalman filter framework6-9 for motion tracking and prediction.

Methods

Motion Prediction Framework:

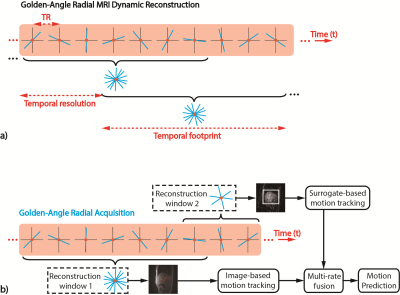
GA Radial MRI: In an IRB-approved study, 2D sagittal liver MRI scans were acquired in 3 healthy subjects at 3T (Prisma, Siemens) using a spoiled gradient echo (GRE) GA radial sequence. Each subject was instructed to perform normal, deep and shallow breathing (9 MRI datasets). Reconstruction windows (RW) were flexibly selected to generate images at different sampling rates (Fig.1).

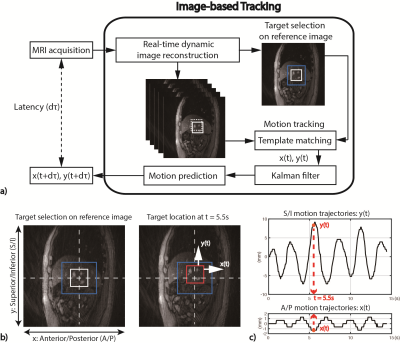
Image-based Tracking: Images with higher SNR and spatial resolution were reconstructed with a wider temporal footprint (RW1). Specific features of the target tissue were identified (Fig.2a). A template-matching algorithm was used to track the 2D translational motion of the target features10 (Fig.2b).

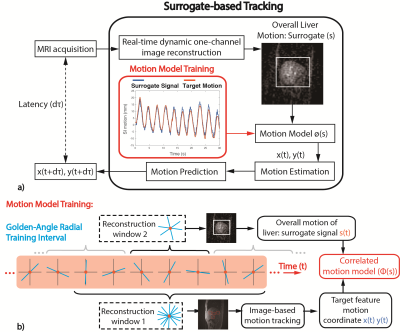
Surrogate-based Tracking: Low-resolution images were also reconstructed with narrow temporal footprint (RW2 in Fig.1b). Overall liver motion was extracted from the images as the surrogate signal to train a motion model for target feature motion estimation (Fig.3). The quadratic model ($$$\phi$$$) was constructed from superior/inferior motion (y) of the target feature and surrogate signal (s)4:

$$y(t)=\phi(s)=as^{2}+bs+c+d\dot{s}+e\dot{s}^{2}$$

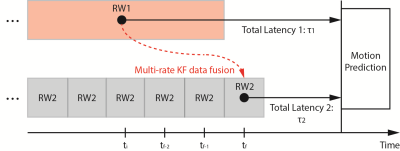
Multi-rate Kalman filter (KF): A data fusion framework using KF11 was established based on the multi-rate characteristics of image-based and surrogate-based tracking (Fig.4a). Surrogate-based tracking was designated as the frequent KF (FKF) agent, which was updated at a higher temporal rate with low latency. Image-based tracking was the infrequent KF (IKF) agent, which was updated at a lower temporal rate with higher latency9. Robustness of motion state estimation using the FKF agent was improved by fusing the estimation from the IKF agent6,7, which improves spatial accuracy of motion prediction11.

Evaluation:

The multi-rate motion prediction framework was implemented offline to simulate real-time processing with GA radial sampling (Fig.4).

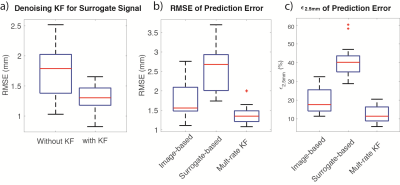
Surrogate-based Tracking: 4 target regions in the liver were selected for image-based tracking and extracted motion coordinates were set as ground truth (yg). A denoising KF was applied to decrease surrogate noise, which is independent of the multi-rate KF, requiring a separate training. Tracking error (TRE) was defined as:

$$TRE(t)=\mid\phi(s(t))-y_{g}(t)\mid$$

Mean differences in root-mean-square error (RMSE, mm) of TRE with and without denoising KF were assessed using one-tailed paired-sample t-test (p<0.05 considered significant)

Motion Prediction: The latencies were calibrated (Fig.4) and prediction results using the proposed multi-rate KF were compared with using only image-based or surrogate-based tracking for 36 target features. The ground truth feature coordinates were extracted at the time point of motion prediction with retrospectively reconstructed high-resolution images. Differences in RMSE and the percentage of prediction error>2.5mm (ε2.5, %) were compared using non-parametric tests (p<0.05 considered significant). The threshold was selected as physicians target lesions with diameter$$$\geq$$$5 mm12.

Results

Surrogate-based Tracking: The mean of RMSE of TRE using denoising KF is significantly lower than the results without using denoising KF (1.350mm versus 1.765mm, p = 0.0062) (Fig.5a).

Motion Prediction: The mean of both RMSE and ε2.5 using multi-rate KF motion prediction were significantly lower than that using only surrogate-based or image-based tracking. In addition, the variance of RMSE using multi-rate KF motion prediction was significantly lower than the other methods; there was no significant difference in variance of ε2.5. among methods (Fig.5b-c).

Discussion

Experimental results provide evidence that the proposed multi-rate motion prediction framework can achieve significantly higher spatial accuracy (RMSE=1.39±0.60 mm) than using only surrogate-based or image-based tracking, and reduce latency compared to image-based tracking. Consistency in motion prediction accuracy is also improved using this multi-rate framework (lower variance in RMSE). Additional model-based processing of surrogate-based tracking has potential to improve the framework. Further work will include more datasets and implement online processing to continue the evaluation of the proposed framework.

Conclusion

In this study, a multi-rate motion prediction framework with GA radial acquisition is proposed to combine the advantages of image-based and surrogate-based motion tracking for real-time MRI guided interventions. The preliminary results demonstrate the feasibility of the proposed multi-rate framework in reducing motion prediction error for low-latency feedback.

Acknowledgements

No acknowledgement found.

References

1. Mikaiel S, Simonelli J, Lee Y, Li X, Lee YS, Lu D, Sung K, Tsao TC, and Wu HH. Real-Time MRI-Guided Targeted Needle Placement During Motion using Rolling Diaphragm Hydrostatic Actuators. Proceedings of the ISMRM 25th Annual Meeting, Honolulu, 2017, p736.

2. Sharp, GC, Jiang SB, Shimizu S, Shirato H. Prediction of respiratory tumour motion for real-time image-guided radiotherapy. Phys Med Biol 2004;49:425–440.

3. Seregni M, Paganelli C, Lee D, Greer PB, Baroni G, Keall PJ, et al. Motion prediction in MRI-guided radiotherapy based on interleaved orthogonal cine-MRI. Phys Med Biol 2016;61:872–887.

4. Paganelli C, Seregni M, Fattori G, Summers P, Bellomi M, Baroni G, et al. Magnetic resonance imaging-guided versus surrogate-based motion tracking in liver radiation therapy: A prospective comparative study. Int J Radiat Oncol Biol Phys 2015;91:840–848.

5. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76.

6. Alexander, HL. State Estimation for Distributed Systems with Sensing Delay. In: SPIE , Orlando, 1991; Data Structures and Target Classification 1470:103–111.

7. Larsen TD, Andersen NA, Ravn O, Poulsen NK. incorporation of time delayed measurements in a discrete-time Kalman filter. IEEE Conf Decis Control 1998;4:3972–7.

8. Gopalakrishnan A, Kaisare NS, Narasimhan S. Incorporating delayed and infrequent measurements in Extended Kalman Filter based nonlinear state estimation. J Process Control 2011;21:119–129.

9. Fatehi A, Huang B. Kalman filtering approach to multi-rate information fusion in the presence of irregular sampling rate and variable measurement delay. J Process Control 2017;53:15–25.

10. Wu HH, Gurney PT, Hu BS, Nishimura DG, McConnell M V. Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three-dimensional cones imaging. Magn Reson Med 2013;69:1083–93.

11. Li X, Mikaiel S, Simonelli J, Lee Y, Tsao TC, and Wu HH. Real-Time Motion Prediction for Feedback Control of MRI-Guided Interventions. Proceedings of the ISMRM 25th Annual Meeting, Honolulu, 2017, p5540.

12. Kim YK, Kim YK, Park HJ, Park MJ, Lee WJ, Choi D. Noncontrast MRI with diffusion-weighted imaging as the sole imaging modality for detecting liver malignancy in patients with high risk for hepatocellular carcinoma. Magn. Reson. Imaging 2014;32:610–618.

Figures

Figure 1 - Proposed motion prediction framework: a) Golden angle (GA) radial spokes were acquired with TR=4.68ms and flip angle=70°. Field of view (FOV) was 300mm×300mm. b) From reconstruction window 1 (RW1), 70 spokes were reconstructed with temporal footprint of 328ms and sliding-window temporal resolution of 131ms to generate images with spatial resolution of 1.56mm×1.56mm for image-based motion tracking of target tissue features. From RW2, 14 spokes were reconstructed with temporal footprint and temporal resolution of 66ms to generate images with low spatial resolution of 4.84mm×4.84mm, which were used to extract the overall liver motion as the surrogate signal.

Figure 2 - Image-based motion tracking: a) Real-time dynamic MRI was reconstructed (Fig.1a) and provided to the image-based motion tracking algorithm to extract target feature motion. Because of the time required for acquisition and reconstruction, target tracking had increased latency. b) The target feature to track was selected on a reference anatomical image (white box) and the expected maximum range of motion was specified (blue box). c) Image-based motion tracking calculate 2D displacement of the target using a template-matching algorithm with least-squares metric.

Figure 3 - Surrogate-based Motion Tracking: a) One receiver channel with the highest contrast near the liver and diaphragm was manually selected and a small interval of GA radial data (e.g., RW2 in Fig.1) was reconstructed to generate low spatial-resolution/high temporal-resolution images. The bulk motion of the whole liver was extracted as the surrogate signal. b) In the training interval, GA radial spokes were retrospectively collected into RW1 and RW2 centered at the same time point. Image-based tracking extracted reference target feature motion coordinates for the corresponding surrogate signal and the parameters of the correlated motion model were trained.

Figure 4 - Multi-rate Kalman Filter (KF) Data Fusion: For the parameters considered in the experiments, the latency of image tracking (τ2) was 264ms and the latency of surrogate tracking (τ1) was 67ms. Image-based tracking results from images corresponding to reconstruction window 1 (RW1) were designated as the infrequent KF (IKF) agent. Surrogate-based tracking results were extracted from RW2 with less latency than RW1 and designated as the frequent KF (FKF) agent. The IKF tracking results at ti were fused with the FKF results at tf using a multi-rate KF6,11, where the measurement matrix and noise were obtained from model calibration.

Figure 5 - Summary of motion prediction results based on 36 target features from 9 datasets: a) RMSE of tracking error of surrogate-based tracking with denoising KF or shows an improvement over without denoising KF. b-c) RMSE and ε2.5 of different motion prediction methods are compared. The mean RMSE and ε2.5 using multi-rate KF prediction was significantly reduced versus surrogate-based and image-based tracking (one-tailed Wilcoxon Signed Rank test p=0.015 and 8.9×10-7 for RMSE; p=4.23×10-5 and 2.68×10-8 for ε2.5, respectively). The RMSE variance using multi-rate KF prediction was significantly reduced (Brown-Forsythe test, p= 0.0001), but ε2.5 variance had no significant difference (p>0.05)

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
4151