Synopsis

A stack of disks trajectory for fast 3D acquisitions with long readouts is introduced and compared to interleaved stack of spiral and Yarn-ball trajectories. Isotropic 1.6 mm whole-brain coverage is achieved in less than a second.

Introduction

MR scanning of 3D volumes in under a second is aimed at in applications like fMRI with high temporal resolution¹. 3D Fourier encoding lends itself to this task: it provides high SNR due to data acquistion from the entire volume, while being amenable to undersampling that makes optimal use of parallel imaging acceleration in all three dimensions. Unfortunately the available 3D encoding strategies require a trade-off between the following desirable characteristics, particularly at medium resolution:

1) average k-space speed close to the maximum k-space speed

2) regular undersampling in the entire 3D k-space

3) favorable PSF due to a benign k-space filter

Stacks of EPIs² do not cover k-space as time efficiently as spirals. Cones and concentric shells³ are inefficient in that they oversample the k-space center and/or waste time by using very different readout lengths albeit TR being determined by the longest interleaf.

Recently the stack of blipped spirals was introduced, acquiring two k planes per spiral shot^4–6. However, it does not allow for more k-space volume within one shot with a benign T₂* weighting over the whole 3D k-space. In this work, a method to acquire an arbitrary number of adjacent planes within one shot is introduced (‘stack of disks’). It covers 3D k-space with high efficiency, uniform sampling density, and smooth T₂* weighting. This trajectory is compared with an interleaved stack of spirals and the Yarn-ball trajectory⁷.

Methods

Hardware:

• Philips 7T Achieva system
• 32 channel head array (Nova Medical)
• 16 ¹⁹F NMR field probes mounted on the head array and a dedicated MR acquisition system⁸

From the probe data, the actual encoding fields up to 2^nd/3^rd order in space were calculated.

Sequence: A GRE sequence with T₂*-contrast was implemented (TE=20ms/28ms). K-space was covered by three different 3D trajectories, designed for an isotropic resolution and whole brain coverage (FOV=24x24x12cm³) applying a total undersampling factor of R=8, cf. Table 1 for acquisition parameters. Resolution is defined by the extent of a sphere in k-space; for the non-spherical trajectories, k­_max was adjusted to sample the identical k-space volume.

1. Stack of disks: 1.6mm resolution, 11 shots, T_AQ=42ms, TR=76 ms
2. Stack of disks: 3mm resolution, 6 shots, T_AQ=19ms, TR=55 ms
3. Interleaved stack: 3mm resolution, 6 shots, T_AQ=20ms, TR=55 ms
4. Yarn-ball: 3mm resolution, 6 shots, T_AQ=21ms, TR = 55ms

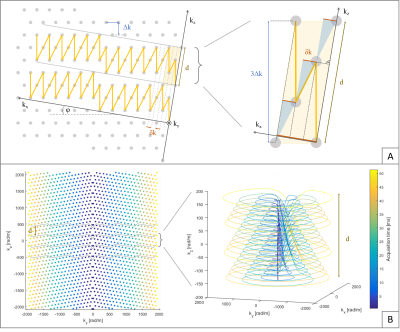
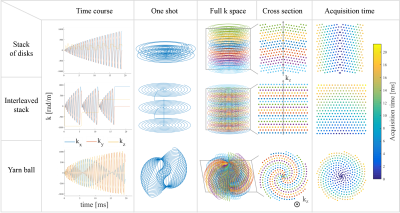
Stack of disks: The hexagonal grid^6,9 formed by a conventional stack of spirals in every plane, which contains the k_z axis, is tilted (Fig.1).

Interleaved stack: Each shot acquires several planes of a spiral stack, one after the other (Fig. 2). In order to obtain a smooth T₂* weighting, an echo time shift has to be introduced.

Yarn-ball (7): Sampling of spherical k-space volume (Fig.2).

Image reconstruction was performed by an iterative conjugate gradient SENSE reconstruction algorithm¹⁰ extended to 3D, including multi-frequency interpolation^11,12 for static off-resonance correction and based on the concurrently monitored trajectories¹³ of 0^th and 1^st spatial order. Off-resonance and coil sensitivity maps were computed from multiecho, multisclice spin-warp pre-scans (6 echoes, TE 4-9 ms, 1x1x1mm³ resolution, R=3 and 1 echo, TE=4ms, 5x5x1mm³ resolution).

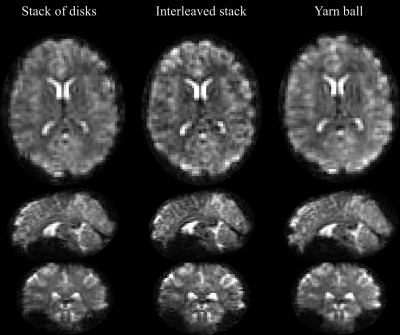
Results

Discussion and conclusion

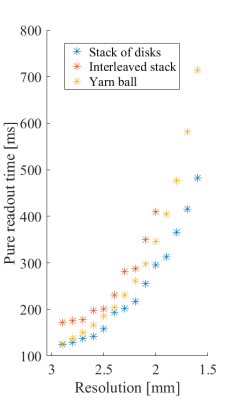
All of the three discussed trajectories exhibit smooth T₂* weighting. However, to accomplish this goal, the interleaved stack trajectory has to introduce a costly echo time shift (here: 25% prolongation), reducing its efficiency (Fig. 3).

The Yarn-ball trajectory loses efficiency by oversampling the poles of the acquired k-space sphere in order to sample densely enough at the equator. Plus, for many shots, it approaches radial sampling in the k_x-k_y plane, thereby oversampling low k_z values. In contrast, the stack of disks trajectory preserves a homogeneous k-space density by sampling spirals on a hexagonal grid. The strategy could equally be applied to EPI trajectories, catching however the same time loss compared to spirals as in 2D.

An advantage of the Yarn-ball trajectory is its reduced sensitivity to flow in any direction, being a potential source of artifacts. Both stack trajectories do need a prephaser gradient in k_z direction. Besides, the Yarn-ball never has to slow down on its k-space path. Aiming for the same, the stack of disks trajectory leaves small undersampled areas at the site of the blips, which could be mitigated by slightly shifting the applied blips for each rotation.

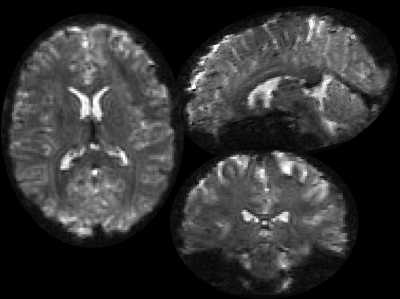
To account for off-resonance and actual gradient dynamics the reconstruction was based on the expanded signal model described above. Whole brain coverage is attained in 330ms at 3mm isotropic resolution (Fig. 4). For higher-resolved applications, Yarn-ball and interleaved stack are not competitive anymore (Fig.3). The stack of disks trajectory covers 1.6mm isotropic resolution in 840ms (Fig. 5), whereas both of the others would require more than a second.

Acknowledgements

References