Synopsis

Acquiring three-dimensional (3D) images in MRI is a time consuming process. The overall duration of acquiring a Nyquist sampled 3D dataset can be significantly shortened by enhancing the efficiency of $$$k$$$-space sampling. This can be achieved by accelerating each $$$k$$$-space read-out and by additionally increasing the coverage of $$$k$$$-space for every trajectory interleave.

In this work, we present a 3D $$$k$$$-space trajectory that is highly accelerated in terms of $$$k$$$-space velocity that leads to a low-discrepant coverage of suchlike using a considerably reduced number of read-outs.

Introduction

Fast volumetric imaging requires efficient $$$k$$$-space sampling in which every interleave contains $$$k$$$-space information of all dimensions and therefore allows for fast 3D partial $$$k$$$-space reconstruction. Present approaches for efficient 3D trajectory design^1,2,3 suffer from long read-out durations and are as a consequence prone to off-resonance effects and low SNR.

We present a 3D ultra-short echo time $$$k$$$-space trajectory that is optimised with respect to $$$k$$$-space velocity, read-out duration, and low-discrepant coverage of $$$k$$$-space.

Methods

For an efficient $$$k$$$-space read-out, parameters considering the properties of a single interleave, as well as the complete trajectory need to be considered.

In the presented approach (PA), a trajectory is obtained by using a Fourier series ansatz for each 'spatial' component of $$$k$$$-space:

$$k_{\phi} = a_0 + \sum_{i=1}^{n}{a_i\cos(iw\phi)+b_i\sin(iw\phi)} \,\,\,\, \text{with} \, \, \phi = x,y,z.$$

Each such generated series is then scaled to achieve a single centre-out interleave. The resulting base trajectory (interleave) is rotated in $$$k$$$-space such that the end points of the interleaves follow a Fibonacci distribution on the unit sphere. The constructed number of Fibonacci points depends on the required number of interleaves in order to fulfil Nyquist's theorem. The Fourier coefficients are then optimised according to the introduced maximisation problem

$$E(X(k_x,k_y,k_z)) = \left (\frac{1}{D} \right )^{\lambda_1} \sum\limits_{j=1}^{N_\text{ro}}{ \left \{ \left ( \left ( \lambda_2\left( \frac{| \sum_i^{|k_{x,j}|}{k_{x,i}} |}{|k_{x,j}|} + \frac{| \sum_i^{|k_{y,j}|}{k_{y,i}} |}{|k_{y,j}|} + \frac{| \sum_i^{|k_{z,j}|}{k_{z,i}} |}{|k_{z,j}|} \right ) \left ( L_{\text{c},j}^{-1} \right )^{\lambda_3} \right ) \left ( T_{\text{acq},j}^{-1} \right )^{\lambda_4} \right ) \frac{\rho_{\text{rel},j}^{\lambda_5}}{N_{\text{ro},j}^{\lambda_6}} \right \}}.$$

The criteria contains properties of the complete trajectory $$$X(k_x,k_y,k_z)$$$ such as the diaphony $$$D$$$⁴, relative $$$k$$$-space density $$$\rho_{\text{rel}}$$$ and total number of read-outs (interleaves) $$$N_{\text{ro}}$$$. The outer sum is a summation over the spatial variation of the coordinates $$$k_x,k_y,k_z$$$ of each rotated base trajectory. A large variation is subjected to reach low-discrepancies for each interleave. This variation is then normalised according to the spatial read-out length $$$L_{\text{c}}$$$ in $$$k$$$-space. The read-out duration $$$T_{\text{acq}}$$$ is introduced as an upper threshold. Finally, the efficiency decreases as the number of read-outs $$$N_{\text{ro}}$$$ increases. The term $$$|k_{\phi,j}|$$$ denotes the number of points forming one interleave. The introduced parameters $$$\lambda_i$$$ allow for a different weighting of each quantity, if desired.

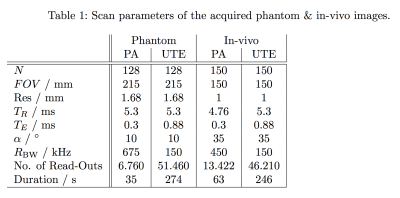
In a final step, the trajectory is optimised with respect to gradient and slew-rate constraints such that maximum $$$k$$$-space velocity is achieved. All read-outs are shuffled randomly for optimised undersampling properties. The optimised trajectory is implemented on a 3T Philips Achieva system and tested on an image quality phantom and in-vivo on a human knee with scan parameters as summarised in table 1.

Results and Discussion

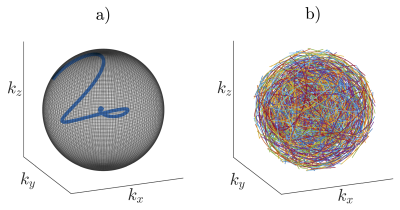
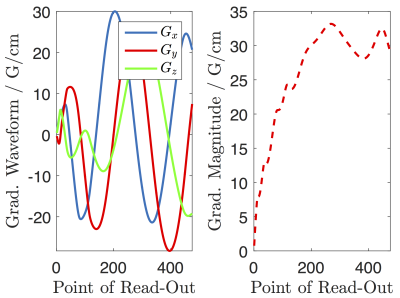
Figure 1 a) shows the first interleave with 1.000 sampling points of the proposed trajectory, while b) shows 250 randomly selected interleaves in order to illustrate the achieved coverage of $$$k$$$-space. The minimisation of the duration of a single interleave is achieved by ensuring maximum gradient amplitude and slew-rate. The resulting gradient waveforms and amplitude of the gradients are shown in figure 2.

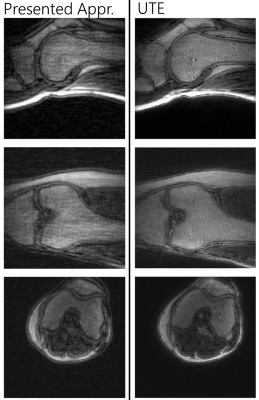
Figure 3 compares 3D images of the image quality phantom acquired with the PA and UTE scan. Acquisition time of the PA scan resulted in 35 s using 6.760 interleaves of 1.2 ms duration, compared to 274 s using 51.460 interleaves of 0.82 ms duration in the UTE scan. In-vivo knee images were acquired within 63 s (figure 4) compared to 246 s for the UTE scan. The PA reconstruction was accomplished using gridding in combination with a Voronoi tessellation⁴.

Compared with a conventional 3D cone trajectory³ with opening angle of 45$$$^\circ$$$, for an equal number of points $$$N$$$, one 3D cone has a weighted diaphony ($$$D/\sqrt{N}$$$) of 0.0156 while it is 0.0141 for one PA interleave with almost similar improvement of $$$\sim$$$10 % for the complete trajectory. With the current implementation, the PA achieves 27 % higher $$$k$$$-space velocities, leading to a huge decrease of the read-out duration of 1.3 ms in comparison to 3 ms for the 3D cones (increased due to the base trajectory's length).

Conclusion

The presented trajectory allows for fast 3D $$$k$$$-space read-outs without compromising $$$k$$$-space coverage. In-vivo and phantom images prove the feasibility of the imaging concept.

The short read-out durations may be advantageous in comparison to the 3D cones approach in terms of image blur, in cases of strictly limited read-out times (e.g. cardiac self-gating), and in cases where fast coverage of $$$k$$$-space is mandatory as e.g. imaging of hyperpolarized media in which only a limited number of excitations can be used.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 667192.

References

1. R. Mir, A. Gueselaga, J. Spiniak, M. Guarini, P. Irarrazaval. Fast Three-Dimensional k-Space Trajectory Design Using Missile Guidance Ideas. Magnetic Resonance in Medicine. 52, 329-336, 2004.

2. S. Sabat, P. Irarrazaval. Three Dimensional K-Space Trajectory Design Using Genetic Algorithms. Proc. Intl. Soc. Mag. Reson. Med. 10, 2002.

3. P. T. Gurney, B. A. Hargreaves, D. G. Nishimura. Design and Analysis of a Practical 3D Cones Trajectory. Magnetic Resonance in Medicine. 55, 575-582, 2006.

4. T. Speidel, J. Paul, S. Wundrak, V. Rasche. Quasi-Random Single-Point Imaging using Low-Discrepancy k-Space Sampling. IEEE Transactions on Medical Imaging. doi:10.1109/TMI.2017.2760919.