4139
MR Image Reconstruction via Denoising (MR-RED)1Department of Biomedical Engineering, The Ohio State University, Columbus, OH, United States
Synopsis
In this work, the feasibility of employing denoising to recover MR images from undersampled data is demonstrated. By embedding denoisers into the Laplacian-based regularization functional and solving the resulting optimization problem, state-of-the-art results are achieved. Performance of several denoisers and compressed sensing methods is compared in four cardiac MRI datasets. We show that denoising-based reconstruction can outperform soft-thresholding-based algorithms in terms of normalized MSE.
Background
Regularized image reconstruction methods, especially ones based on the concepts of sparsity and low-rank, have enabled image recovery from highly undersampled MRI data. Recently, it has been shown that state-of-the-art results can be achieved by simply embedding image denoisers into the image reconstruction1. A typical implementation of this approach, termed Plug-and-Play Prior (PPP), alternates between data fitting and denoising and therefore admits a structure fit for ADMM optimization. However, the underlying cost function and convergence characteristics of PPP are unknown. Through clever choice of objective function, recent research has proposed a convex cost function that allows for regularization by any denoising function that meets a two loose criteria2. Leveraging these recent developments, we propose a reconstruction framework, called MR Image REconstruction via Denoising (MR-RED), and demonstrate its feasibility by recovering cardiac MR images from retrospectively undersampled data.Methods
The vast majority of compressed sensing inspired MRI acceleration techniques utilize an $$$\ell_2-\ell_1$$$ cost function such as $$\arg\min_x ||Ax-y||_2^2 + \lambda||\Psi x||_1,\,\,\,\,(\text{Eq.1})$$ where $$$A$$$ is the forward operator, $$$X$$$ is the MR image, $$$y$$$ is the k-space data, and $$$\Psi$$$ is a sparsifying transform. Many fast algorithms, such as FISTA, exist to solve this optimization problem, and almost all these algorithms require applying the adjoint of the sparsifying transform, $$$\Psi^H$$$. Despite the amazing success of this $$$\ell_2-\ell_1$$$ formulation, soft thresholding on transform coefficients is just a subset of all image denoising options in the literature. Many state-of-the-art denoising methods involve complicated and non-local functions where the adjoint may be difficult or impossible to describe, making gradient based methods intractable or only loosely connected to the original cost function.
In contrast, MR-RED is based on the following cost function2 $$\arg\min_x ||Ax-y||_2^2 + \lambda_R x^H(x-f(x)),\,\,\,\,(\text{Eq. 2})$$ where $$$f(x)$$$ is a denoising function and $$$x^H$$$ is the conjugate transpose of $$$x$$$. The above cost function can be applied for any denoising function $$$f(x)$$$ meeting loose restrictions $$$cf(x) = f(cx)$$$ for scaler $$$c\geq0$$$ and $$$|| f(x) ||_2 \leq ||x||_2$$$2. Under these conditions, the directional derivative $$$\nabla_x f(x)x=f(x)$$$, greatly simplifying gradient based solvers for the MR-RED cost function. In this work, we use an ADMM formulation to solve the MR-RED cost function as described in2.
Data acquisition and processing- Four fully sampled breath-held cine datasets were acquired from four healthy volunteers on a 1.5 T (Avanto, Siemens Healthcare, Erlangen, Germany) system using a balanced SSFP acquisition and an 18 channel cardiac array. Other imaging parameters included: TE/TR 1.1/2.6 ms, flip angle 53 degrees, spatial resolution 2.5 mm or better, temporal resolution 40 ms or better. All data were retrospectively downsampled using VISTA3 for acceleration rates R = 2, 4, 6, …26. Normalized mean squared error (NMSE) was computed for each recovered image. NMSE is defined as $$\text{NMSE} = 20\text{log}\left( \frac{|| x-\hat{x}||_2}{||x||_2} \right) $$ where $$$x$$$ is the fully sampled image and $$$\hat{x}$$$ is the recovered image.
We compared the following five methods for image recovery: CG-SENSE (unregularized SENSE), NWT CS (Eq. 1 with $$$\Psi$$$ being the nondecimated discrete wavelet transform, FISTA solver); NWT-m CS (same as NWT CS but three different regularization weights were manually tuned. One weight for the approximate coefficents subband, one for low temporal frequency subbands, and one for high temporal frequency subbands); MR-RED WT ST (Eq. 2 with denoising based on soft-thresholing (ST) of decimated wavelet transform); MR-RED Median (Eq. 2 with denoising based on 3x3x3 spatio-temporal median filtering); and MR-RED Wiener, where adaptive Wiener filtering was applied locally on 5x5x5 spatio-temporal patches. Each MR-RED method requires manual tuning of the parameter $$$\lambda_R$$$. In addition, MR-RED may require a tuning parameter, $$$\sigma_f$$$, for the specific denoiser being used. MR-RED Median requires no $$$\sigma_f$$$, MR-RED WT ST requires three different values of $$$\sigma_f$$$ for different subbands, and MR-RED Wiener requires a single $$$\sigma_f$$$.
Results and Discussion
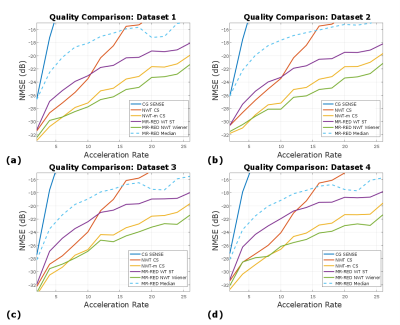
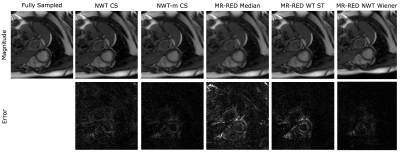
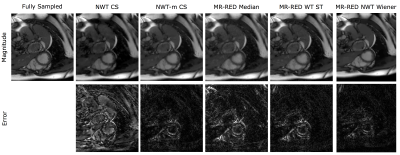
In Figure 1, NMSE is plotted vs. acceleration rate for all four datasets and each image recovery method. Figure 2 contains reconstructed images and error images compared to fully sampled data for acceleration rate R=10. Figure 3 contains similar images at R=20. MR-RED WT ST performs 4-5 dB worse than NWT based methods. MR-RED Wiener outperforms all other techniques for R>6 while only requiring two tuning parameters $$$\lambda_R$$$ and $$$\sigma_f$$$ (as opposed to NWT-m CS which requires three tuning parameters for satisfactory performance).Conclusion
We present the MR-RED method and show the potential of new denoising-based reconstruction that can outperform traditional soft-thresholding based algorithms. In future research, we will explore MR-RED with a more extensive list of denoisers and with prospectively undersampled data.Acknowledgements
This work was partially funded by NIH grants R01HL135489.References
[1] Venkatakrishnan, et al, Plug-and-Play priors for model based reconstruction. GlobalSIP. 2013 doi:10.1109/GlobalSIP.2013.6737048
[2] Romano, et al, The Little Engine that Could: Regularization by Denoising (RED), to appear in SIAM Journal on Imaging Sciences, 2017.
[3] Ahmad R. et al. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. Magn Reson Med. 2015;74(5):1266-1278.
Figures